风驰电掣云端飘,相机无法对上焦
- 1.视觉伺服分类
- 2.视觉伺服中的坐标系
- 3.成像模型推导
- 4.IBVS理论推导
- 5.IBVS面临的挑战
- 6.visp 实践
- 参考文献
1.视觉伺服分类
控制量是在图像空间中推导得到还是在欧式空间中推导得到,视觉伺服又可以分类为基于位置(PBVS)和基于图像的(IBVS)视觉伺服。

2.视觉伺服中的坐标系
- 概述
世界坐标系W:用于测量(估计)飞机、机器人的位姿(位置和姿态)。
飞机机体坐标系B:最终运动控制量应转换到这个坐标系。
目标机体坐标系O:用于描述目标物体与相机间的位姿,用于描述相机坐标系和目标物体机体坐标系之间的位姿关系。
相机坐标系C:是推导IBVS最重要的坐标系。
图像坐标系I:是描述特征点运动状态的坐标系。
像素坐标系P:最终的图像数据最终以该坐标系的形式存储信息。 - 表示
W 即 world,表示世界坐标系,E即 end,表示末端坐标系,类似还有I表示 image,O表示 object,C 表示 Camera等。而各种坐标系齐次变换矩阵T的左上标表示转换后的坐标系,右下标表示转换前的坐标系。如 c T e ^{c}T_e cTe或 c V e ^{c}V_e cVe表示从末端坐标系E到相机坐标系C的坐标变换矩阵或称为齐次变换矩阵(齐次变换矩阵即旋转变换和位移变换融合到了一个矩阵当中)。

3.成像模型推导
-
相关概念:透视投影模型。
-
关于透视投影这篇文章讲的很好: 深蓝AI:经典干货|相机模型与张氏标定。参考了这篇文章。
-
小孔成像模型
光心位于成像平面的前方,成倒立的像,这样不方便IBVS的推导。

-
透视投影模型
光心位于成像平面的后方,成正立的实像,更符合实际成像过程,方便IBVS的推导。

-
世界系、相机系、图像系、像素系的轴向、原点位置示意图

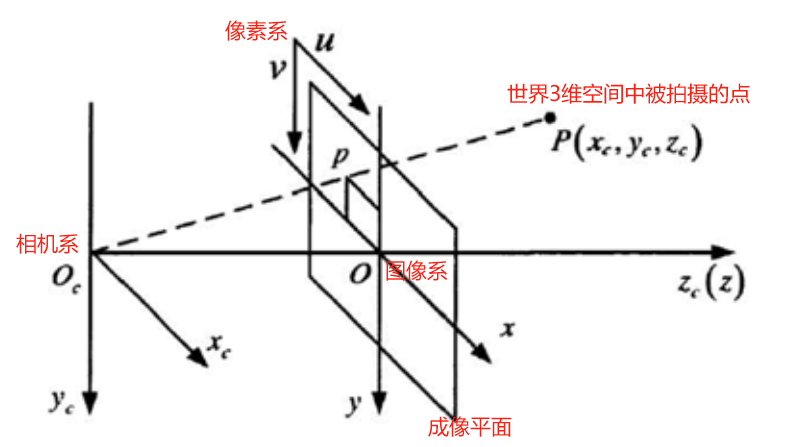

相机系记作Oc-XcYcZc.
图像系记作o-xy.
像素系记作o-uv.
相机系的原点在光心,Xc轴水平向右,Yc轴竖直向下,Zc轴水平向前。
图像坐标系的原点在Zc轴与成像平面的交点处,x、y轴分别与Xc、Yc轴同向。
像素坐标系的原点在成像平面的左上角,u、v轴分别与图像系的x、y轴同向。
图像系原点在像素系中的坐标为【u0,v0】,也被称为主点坐标。
相机系原点到成像平面的距离为 f,即焦距。 -
像素系坐标与图像系坐标间的关系
{ u = x d x + u 0 = p x + u 0 v = x d x + u 0 = p x + u 0 (式 1 ) \begin{cases} u=\frac x {dx}+u_0=p_x+u_0 \\ v=\frac x {dx}+u_0=p_x+u_0 \end{cases}(式1) {u=dxx+u0=px+u0v=dxx+u0=px+u0(式1)
其中:
[u0,v0]是图像系原点在像素系中的坐标;
px,py是图像系中 xy 轴的单位长度对应的像素个数;
uv是像素系中的坐标;
xy是图像系中的坐标。 -
图像系坐标与相机系坐标间的关系
{ x = f Z X y = f Z Y (式 2 ) \begin{cases} x=\frac f {Z}X \\ y=\frac f {Z}Y \end{cases}(式2) {x=ZfXy=ZfY(式2)
其中:
f f f 是相机焦距;
x y xy xy 是图像系中的坐标;
X Y Z XYZ XYZ 是目标点在相机系中的坐标。 -
相机内参
(式1)、(式2) 提到的参数 u 0 , v 0 , p x , p y u_0,v_0,px,p_y u0,v0,px,py 被称为相机的内参,通过相机标定得到。
4.IBVS理论推导

问题描述:
假设在世界3维空间中有一点P,
在相机系中的坐标记作 [ X , Y , Z ] [X,Y,Z] [X,Y,Z],
在图像系中的坐标记作 [ x , y ] [x,y] [x,y],
在像素系中的坐标记作 [ u , v ] [u,v] [u,v]。
记相机的6自由度运动速度矢量(相机坐标系的速度矢量)为:
V c = [ v x , v y , v z , w x , w y , w z ] T (式 3 ) V_c=[v_x,v_y,v_z,w_x,w_y,w_z]^T(式3) Vc=[vx,vy,vz,wx,wy,wz]T(式3)
根据物体的旋转运动和直线运动的经典理论公式,可得到点P在相机系中的运动方程为:
[ X ˙ Y ˙ Z ˙ ] = − [ v x v y v z ] − [ w x w y w z ] × [ X Y Z ] (式 4 ) \begin{bmatrix} \dot{X} \\ \dot{Y} \\ \dot{Z} \end{bmatrix} = - \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix} - \begin{bmatrix} w_x \\ w_y \\ w_z \end{bmatrix} \times \begin{bmatrix} {X} \\ {Y} \\ {Z} \end{bmatrix}(式4) X˙Y˙Z˙ =− vxvyvz − wxwywz × XYZ (式4)
注意:因为 V c = [ v x , v y , v z , w x , w y , w z ] T V_c=[v_x,v_y,v_z,w_x,w_y,w_z]^T Vc=[vx,vy,vz,wx,wy,wz]T是相机的速度矢量,正好与点P的速度矢量相反,因此(式4)右边取的是负号!!
将(式2)对时间求导可得:
{ x ˙ = X ˙ / Z − X Z ˙ / Z 2 y ˙ = Y ˙ / Z − Y Z ˙ / Z 2 (式 5 ) \begin{cases} \dot{x}=\dot{X}/Z-X\dot{Z}/Z^2\\ \dot{y}=\dot{Y}/Z-Y\dot{Z}/Z^2\\ \end{cases}(式5) {x˙=X˙/Z−XZ˙/Z2y˙=Y˙/Z−YZ˙/Z2(式5)
将(式2)和(式4)代入(式5)可得:
{ x ˙ = − v x / Z + x v z / Z + x y w x − ( 1 + x 2 ) w y + y w z y ˙ = − v y / Z + y v z / Z − x y w y + ( 1 + y 2 ) w x − x w z (式 6 ) \begin{cases} \dot{x}=-v_x/Z+xv_z/Z+xyw_x-(1+x^2)w_y+yw_z\\ \dot{y}=-v_y/Z+yv_z/Z-xyw_y+(1+y^2)w_x-xw_z\\ \end{cases}(式6) {x˙=−vx/Z+xvz/Z+xywx−(1+x2)wy+ywzy˙=−vy/Z+yvz/Z−xywy+(1+y2)wx−xwz(式6)
写成矩阵形式:
s ˙ = [ x ˙ y ˙ ] = L s V c (式 7 ) \dot{s}= \begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix} =L_sV_c(式7) s˙=[x˙y˙]=LsVc(式7)
其中 s s s 被称为视觉特征, L s L_s Ls被称为图像雅可比矩阵或相互作用矩阵:
L s = [ − 1 / Z 0 x / Z x y − ( 1 + x 2 ) y 0 − 1 / Z y / Z 1 + y 2 − x y − x ] (式 8 ) L_s= \begin{bmatrix} -1/Z&0&x/Z&xy&-(1+x^2)&y \\ 0&-1/Z&y/Z&1+y^2&-xy&-x \end{bmatrix} (式8) Ls=[−1/Z00−1/Zx/Zy/Zxy1+y2−(1+x2)−xyy−x](式8)
记视觉特征 s s s的期望值为 s d s_d sd,则视觉特征误差为:
s e = s − s d (式 9 ) s_e=s-s_d(式9) se=s−sd(式9)
因为 s d s_d sd是常量因此有:
s ˙ d = 0 (式 10 ) \.s_d=0(式10) s˙d=0(式10)
将(式9)对时间求导,得到误差系统的状态空间方程:
s ˙ e = s ˙ − s ˙ d = L s V c (式 11 ) \.s_e=\.s-\.s_d=L_sV_c(式11) s˙e=s˙−s˙d=LsVc(式11)
设计一个控制律 V c Vc Vc使得(式11)表示的误差系统的全部状态随着时间呈指数衰减到0,即控制律使得最终的误差系统变成如下形式:
s ˙ e = − λ s e (式 12 ) \.s_e=-\lambda s_e(式12) s˙e=−λse(式12)
那么可以反推出控制律:
V c = − λ L s + s e (式 13 ) V_c=-\lambda L_s^+ s_e(式13) Vc=−λLs+se(式13)
其中 L s + L_s^+ Ls+是 L s L_s Ls的广义逆矩阵, λ \lambda λ是一个常量。
待续…
5.IBVS面临的挑战
- 计算 L s + L_s^+ Ls+时会产生奇异值。
- L s L_s Ls不容易得到, L s L_s Ls的几种计算方式请参考:https://zhuanlan.zhihu.com/p/422634446
- 待续…
6.visp 实践
- cJc :相机坐标系的运动控制自由度,可以看作是运动控制自由度雅可比矩阵。
- L:图像雅可比矩阵,相互作用矩阵
- J1:task雅可比矩阵
- signInteractionMatrix:相互作用矩阵的符号,1 for eye-in-hand, -1 for eye-to-hand
- inversionType:指定求广义逆矩阵还是求转置矩阵
- Transpose matrix:转置矩阵
- Inverse matrix:逆矩阵
- task Jacobian 是什么?J1???
V c = − λ L ^ s + e V_c = -\lambda {\widehat {\bf L}}^{+}_{s} {\bf e} Vc=−λL s+e,得到的控制律 V c V_c Vc是相机系的运动矢量!
V e = − λ ( L ^ s c V e ∗ e J e ) + e {V_e }= -\lambda \left( {{\widehat {\bf L}}_{s} {^c}{\bf V}_e* {^e}{\bf J}_e} \right)^{+} {\bf e} Ve=−λ(L scVe∗eJe)+e,得到的控制律 V e V_e Ve是终端系的运动矢量!
其中 L ^ s \widehat {L}_s L s是 L s L_s Ls的估计值!
why ??
推导如下:
s ˙ = L s V c \dot{s}=L_sV_c s˙=LsVc
记终端系的速度矢量为 V e V_e Ve,终端系到相机系的坐标变换矩阵为 c V e ^cV_e cVe,允许控制的速度矢量自由度记为 e J e ^eJe eJe,则:
s ˙ = L s V c = L s c V e e J e V e \dot{s}=L_sV_c=L_s^cV_e{^eJe}V_e s˙=LsVc=LscVeeJeVe
那么控制率就变成了:
V e = − λ ( L s c V e e J e ) − 1 V_e=-\lambda (L_s{^cV_e}^eJe)^{-1} Ve=−λ(LscVeeJe)−1
对于无人机视觉伺服, c V e ^cV_e cVe即飞机机体坐标系FRD到相机系RDF的齐次变换矩阵(坐标变换)!!!!
参考文献
https://zhuanlan.zhihu.com/p/422634446
https://zhuanlan.zhihu.com/p/389903710
深蓝AI:经典干货|相机模型与张氏标定
硕士论文:基于无标定视觉伺服的定位研究-王博