目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
5.完整程序
1.程序功能描述
基于信息论的高动态范围图像评价算法matlab仿真,利用一种自然图像的概率模型对图像的熵与成像动态范围之间的关系进行了数值模拟,得到了具有普遍意义上的理想成像动态范围的计算公式,公式指出了对自然景物完善成像所需的最大动态范围;给出了图像熵与动态范围之间的关系。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行
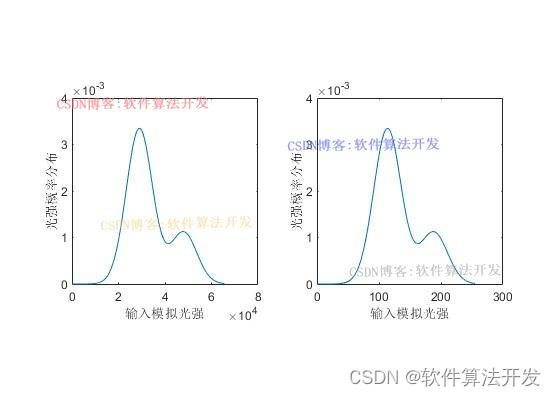
入射的物方景物光强概率分布采用式所述的双高斯分布模型。如图2所示的,其中光强范围
规定为[1:65535]。
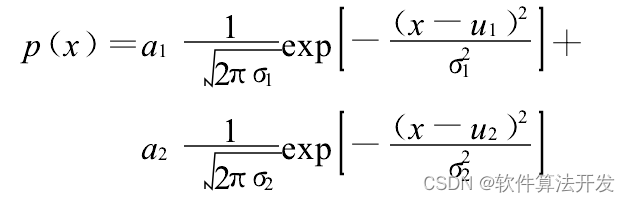
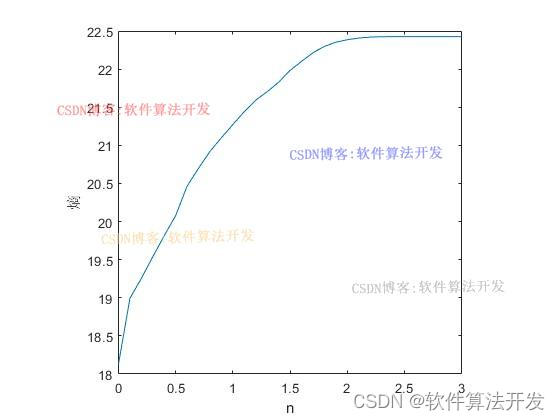
从该图可以明确看到在[μ-3σ,μ+3σ]时图像的熵渐趋于稳定。即此时的系统动态范围可以认为已经足够对当前景物成像。
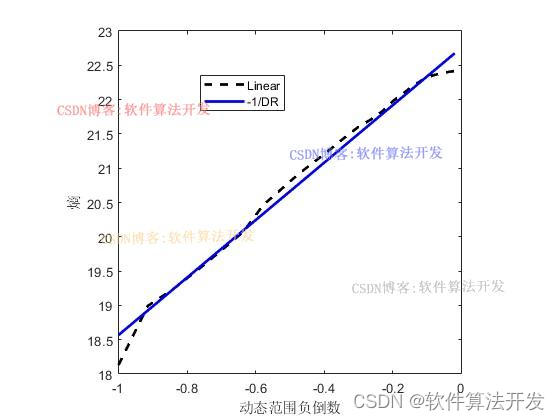
可以看到T与J存在着近似线性的关系,对二者进行线性拟合,得到二者之间的关系。这样,就可以得到成像系统动态范围DR与图像的熵之间的关系.
(完整程序运行后无水印)
3.核心程序
...............................................................
% 图像裁剪处理,限制像素值在[omin, omax]之间
K0 = 0.8;
[R,C] = size(im);
im2 = im;
for i = 1:Rfor j = 1:Cif im(i,j) > omaxim2(i,j) = K0*omax;endif im(i,j) <= omax & im(i,j) >= ominim2(i,j) = K0*im(i,j);end if im(i,j) < ominim2(i,j) = K0*omin;end end
end
im3 = im2;
% 计算裁剪后图像的熵
[row,col] = size(im3);
[count,x] = imhist(im3);
total = row*col;
entropy1 = 0;
for i=1:256 p(i)=count(i)/total; if p(i)~=0 logp(i)=log2(p(i)); entropele=-p(i)*logp(i); entropy1=entropy1+entropele; end
end [row,col] = size(im);
[count,x] = imhist(im);
total = row*col;
entropy = (1-K0)*entropy1 + K0*entropy2;% 结合裁剪图像熵与原始图像熵计算最终熵值
16_044m4.本算法原理
高动态范围图像(High Dynamic Range Imaging, HDR)相较于传统的低动态范围图像(Low Dynamic Range, LDR),能够呈现更广阔的亮度范围和色彩细节,这对于摄影、电影制作、医疗成像等多个领域至关重要。评价HDR图像的质量是一项复杂任务,因为它不仅要考虑图像的客观属性,还要顾及人的主观感受。基于信息论的方法,特别是利用熵和互信息等概念,为HDR图像评价提供了一个理论基础,旨在量化图像的信息内容、细节保留以及视觉感知质量。
信息论是研究信息的量化、存储、传输和处理的学科,由克劳德·香农创立。其中,熵(Entropy)是衡量信息不确定性的度量,而互信息(Mutual Information)则衡量两个随机变量之间的相互依赖程度。

在HDR图像评价中,信息论方法主要通过以下几个方面发挥作用:
局部熵:考虑到人眼对图像不同区域的敏感度不同,局部熵被用来评估图像的局部信息丰富度。对于图像的每个像素块,计算其灰度直方图的熵,以此反映局部细节的复杂度。
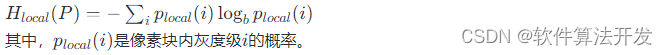
全局熵:衡量整幅图像的信息量,反映了图像整体的动态范围和对比度。对于HDR图像,高全局熵通常意味着更丰富的细节和更宽的亮度范围。

HDR图像的亮度和对比度是决定图像质量的关键因素。通过分析不同亮度区间内的熵分布,可以评估图像在不同亮度层次上的信息保留情况。对比度的熵分析则关注于不同亮度区域间的边界信息,高对比度边界通常携带更多信息,有助于提高图像的可识别性和视觉质量。
5.完整程序
VVV