介绍
石墨烯算法是一种新兴的优化算法,灵感来自于石墨烯的结构和特性。石墨烯是一种由碳原子构成的二维蜂窝状晶格结构,具有优异的机械、电学和热学性能。石墨烯算法通过模拟石墨烯原子之间的相互作用和迁移,来求解复杂的优化问题
基本概念
石墨烯的结构:
石墨烯由碳原子组成,每个碳原子与其他三个碳原子通过共价键连接,形成一个蜂窝状的二维晶格结构。这种结构使得石墨烯具有非常高的强度和导电性。
石墨烯算法的灵感:
石墨烯算法借鉴了石墨烯的这种晶格结构和原子迁移特性,通过模拟碳原子在二维平面上的移动和相互作用,来寻找优化问题的最优解
算法步骤
初始化:
初始化一组解,称为“碳原子”,并将它们随机分布在二维平面上。这些解代表了问题的初始解集。
评估适应度:
计算每个碳原子的适应度值,根据适应度函数评估每个解的优劣。
更新位置:
根据某种规则更新碳原子的位置,模拟碳原子在二维平面上的迁移。这种迁移可以通过模拟退火、粒子群算法或其他元启发式方法来实现。
局部搜索:
在每次迭代中,对每个碳原子进行局部搜索,进一步优化其位置。局部搜索可以通过梯度下降或其他局部优化方法来实现。
选择与替换:
根据适应度值选择较优的碳原子,并用它们替换较差的碳原子,形成新的解集。
迭代:
重复上述步骤,直到达到预定的迭代次数或满足收敛条件。
石墨烯算法的优点
全局搜索能力强:
石墨烯算法能够在广阔的搜索空间中找到全局最优解,避免陷入局部最优。
收敛速度快:
通过模拟碳原子的快速迁移和局部优化,石墨烯算法具有较快的收敛速度。
适应性强:
石墨烯算法可以处理各种类型的优化问题,包括连续、离散和混合优化问题
石墨烯算法的应用
石墨烯算法可以应用于许多实际问题,如:
工程优化:
用于结构优化、路径规划、资源分配等工程领域的问题。
机器学习:
用于神经网络训练、特征选择、超参数优化等机器学习任务。
数据挖掘:
用于聚类分析、关联规则挖掘、分类等数据挖掘任务。
金融优化:
用于投资组合优化、风险管理、期权定价等金融领域的问题
本文代码
定义期权定价模型:我们可以使用Black-Scholes模型来计算欧式期权的理论价格。
设计石墨烯优化算法:模拟石墨烯原子之间的相互作用和迁移,以找到最优的期权定价参数。
整合并实现:将期权定价模型和石墨烯算法整合在一起。
期权定价模型(Black-Scholes)
Black-Scholes模型用于计算欧式看涨期权(Call Option)和看跌期权(Put Option)的价格:
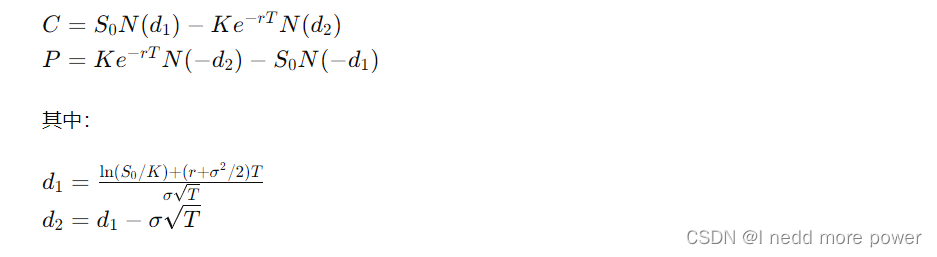
核心代码
Graphene_Option_Pricing.m
function [best_params, best_fitness] = Graphene_Option_Pricing(S0, K, r, T, market_price, is_call)% 参数初始化dim = 1; % 需要优化的参数维度:波动率σlower_bound = [0.01]; % 下界:波动率upper_bound = [1.0]; % 上界:波动率max_iter = 500; % 最大迭代次数pop_size = 30; % 种群大小% 适应度函数:计算Black-Scholes理论价格与市场价格的均方误差fitness_func = @(params) calculate_fitness(params, S0, K, r, T, market_price, is_call);% 石墨烯优化算法[best_params, best_fitness] = Graphene_Optimization(dim, lower_bound, upper_bound, max_iter, pop_size, fitness_func);disp('Best parameters found:');disp(best_params);disp('Fitness of best parameters:');disp(best_fitness);% 验证找到的最佳波动率参数optimal_sigma = best_params(1);% 使用最佳波动率参数计算期权价格if is_callmodel_price = Black_Scholes_Call(S0, K, r, optimal_sigma, T);elsemodel_price = Black_Scholes_Put(S0, K, r, optimal_sigma, T);end% 打印模型价格和市场价格进行比较disp('Optimal sigma:');disp(optimal_sigma);disp('Model option price with optimal sigma:');disp(model_price);disp('Market option price:');disp(market_price);
endfunction fitness = calculate_fitness(params, S0, K, r, T, market_price, is_call)sigma = params(1);if is_callmodel_price = Black_Scholes_Call(S0, K, r, sigma, T);elsemodel_price = Black_Scholes_Put(S0, K, r, sigma, T);end
endfunction C = Black_Scholes_Call(S0, K, r, sigma, T)d1 = (log(S0 / K) + (r + 0.5 * sigma^2) * T) / (sigma * sqrt(T));d2 = d1 - sigma * sqrt(T);C = S0 * normcdf(d1) - K * exp(-r * T) * normcdf(d2);
endfunction P = Black_Scholes_Put(S0, K, r, sigma, T)d1 = (log(S0 / K) + (r + 0.5 * sigma^2) * T) / (sigma * sqrt(T));d2 = d1 - sigma * sqrt(T);P = K * exp(-r * T) * normcdf(-d2) - S0 * normcdf(-d1);
endfunction [best_solution, best_fitness] = Graphene_Optimization(dim, lower_bound, upper_bound, max_iter, pop_size, fitness_func)% 初始化positions = lower_bound + (upper_bound - lower_bound) .* rand(pop_size, dim);% 主循环for iter = 1:max_iter% 更新位置for i = 1:pop_size% 模拟碳原子的迁移new_position = positions(i, :) + rand(1, dim) .* (best_solution - positions(i, :));new_position = max(min(new_position, upper_bound), lower_bound);new_fitness = fitness_func(new_position);% 局部搜索if new_fitness < fitness(i)positions(i, :) = new_position;fitness(i) = new_fitness;end% 更新最优解if new_fitness < best_fitnessbest_fitness = new_fitness;best_solution = new_position;endend% 记录迭代过程中的最优值(可选)disp(['Iteration ', num2str(iter), ': Best Fitness = ', num2str(best_fitness)]);end
endrun_graphene_option_pricing.m
function run_graphene_option_pricing% 示例使用
S0 = 100; % 当前股票价格
K = 100; % 执行价格
r = 0.05; % 无风险利率
T = 1; % 到期时间(年)
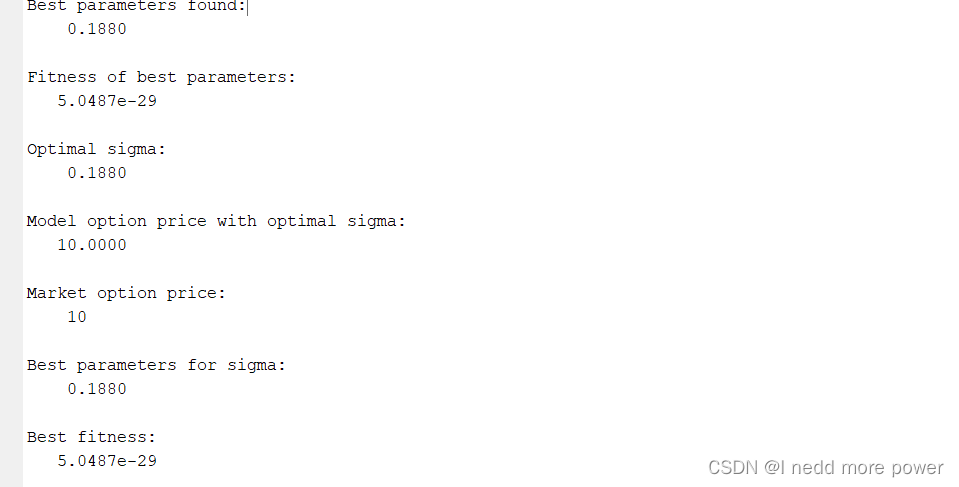
market_price = 10; % 市场期权价格
is_call = true; % 是否为看涨期权[best_params, best_fitness] = Graphene_Option_Pricing(S0, K, r, T, market_price, is_call);
disp('Best parameters for sigma:');
disp(best_params);
disp('Best fitness:');
disp(best_fitness);end
说明
初始化:初始化石墨烯算法的种群,包括参数的上下界、最大迭代次数和种群大小。
适应度函数:计算理论价格和市场价格之间的均方误差。
Black-Scholes模型:计算欧式看涨期权和看跌期权的价格。
石墨烯优化算法:通过模拟石墨烯原子的迁移和相互作用,找到最佳的期权定价参数。
结果输出:输出最佳参数和相应的适应度值。
效果
完整代码获取
微信扫一扫,回复"石墨烯优化算法"即可查看完整代码