目录
一、实验目的
二、实验说明
三、实验过程
3.1 创建蒙特卡罗算法源码
3.2 Makefile的创建与编译
3.3 主机文件配置与运行监测
四、实验结果与分析
4.1 原教程对应的实验结果
4.2 改进后的实验结果
五、实验思考与总结
5.1 实验思考
5.2 实验总结
END~
一、实验目的
1.1 掌握蒙特卡罗算法程序的编写以及编译运行。
1.2 实现在多台主机上编译运行蒙特卡罗算法的程序。
二、实验说明
华为鲲鹏云主机、openEuler 20.03 操作系统;
四台主机名称及ip地址如下:
122.9.37.146 zzh-hw-0001
122.9.43.213 zzh-hw-0002
116.63.11.160 zzh-hw-0003
116.63.9.62 zzh-hw-0004
三、实验过程
3.1 创建蒙特卡罗算法源码
首先创建 MonteCarlo 目录存放该程序的所有文件, 并进入 MonteCarlo 目录(四台主机都执行),具体通过输入如下命令:
mkdir /home/zhangsan/MonteCarlo
cd /home/zhangsan/MonteCarlo
然后通过输入vim MonteCarlo.cpp创建 MonteCarlo 源码 MonteCarlo.cpp(四台主机都执行)。代码输入结束后,输入:wq完成文件保存。部分代码如下:
①圆周率计算关键代码
truct timeval start, stop;
gettimeofday(&start, NULL);
MC::PI::calPiRets *rets;
rets = MC::RunMC<MC::PI::calPiArgs, MC::PI::calPiRets>(n);
#pragma omp parallel for reduction(+ : count)
for (int i = 0; i < n; i++) {if (rets[i].hit) {count += 1.0;}
}
double pi_estimate = count * 4.0 / n;
gettimeofday(&stop, NULL);
double elapse = (stop.tv_sec - start.tv_sec) * 1000 + (stop.tv_usec - start.tv_usec) / 1000;
cout << "采样数为 " << n << " 时圆周率计算耗时: " << elapse << " ms" << endl;②定积分计算关键代码
gettimeofday(&start, NULL);MC::Integral::val *rets2;rets2 = MC::RunMC<MC::Integral::variable, MC::Integral::val>(n);count = 0;
#pragma omp parallel{
#pragma omp for reduction(+ : count)for (int i = 0; i < n; i++) {count += rets2[i].y;} }
//cout << "Integral = " << double(count / n) << endl;gettimeofday(&stop, NULL);elapse = (stop.tv_sec - start.tv_sec) * 1000 +(stop.tv_usec - start.tv_usec) / 1000;
cout << "采样数为 " << n << " 时多维积分计算耗时: " << elapse << " ms" << endl;
接下来输入vim MonteCarlo.h继续创建 MonteCarlo 头文件 MonteCarlo.h(四台主机都执行)。
3.2 Makefile的创建与编译
首先输入vim Makefile创建Makefile文件,并输入如下内容:
CC = g++
CCFLAGS = -I . -O2 -fopenmp
LDFLAGS = # -lopenblas
all: montecarlo
montecarlo: MonteCarlo.cpp${CC} ${CCFLAGS} MonteCarlo.cpp -o montecarlo ${LDFLAGS}
clean:rm montecarlo输入:wq完成文件保存后输入make开始进行编译,结果如下

生成了可执行文件montecarlo .
3.3 主机文件配置与运行监测
首先输入vim /home/zhangsan/MonteCarlo/hostfile进行主机文件配置,内容如下:
zzh-hw-0001:2
zzh-hw-0002:2
zzh-hw-0003:2
zzh-hw-0004:2
然后输入vim run.sh进行脚本文件编写
app=$1
if [ $app = "montecarlo" ]; then./montecarlo ${2} ${3}
fi此处对命令行输入进行了改动,将采样点数作为作为可变参数放入命令行。原教程中采样点数固定为8000000。对此部分进行改动,也是便于研究采样点数对实验结果的影响。
然后分别执行以下命令,查看蒙特卡罗算法运行结果(只需要在任意一台主机上执行),结果在下一部分进行展示。
四、实验结果与分析
4.1 原教程对应的实验结果
受篇幅限制仅展示处理机数量为1和8的结果,1-8 数字表示启动处理的进程数量。

从结果中可以看出出蒙特卡罗算法程序已经在集群中并行运行起来。其中第一行输出代表的是蒙特卡罗算法统计耗时,第二行输出代表的是 Integral 统计耗时。可以得出结论,随着进程数量的增加,耗时越来越少。
4.2 改进后的实验结果
命令行输入bash run.sh montecarlo a b
a为进程数量,b为设置的采样点数
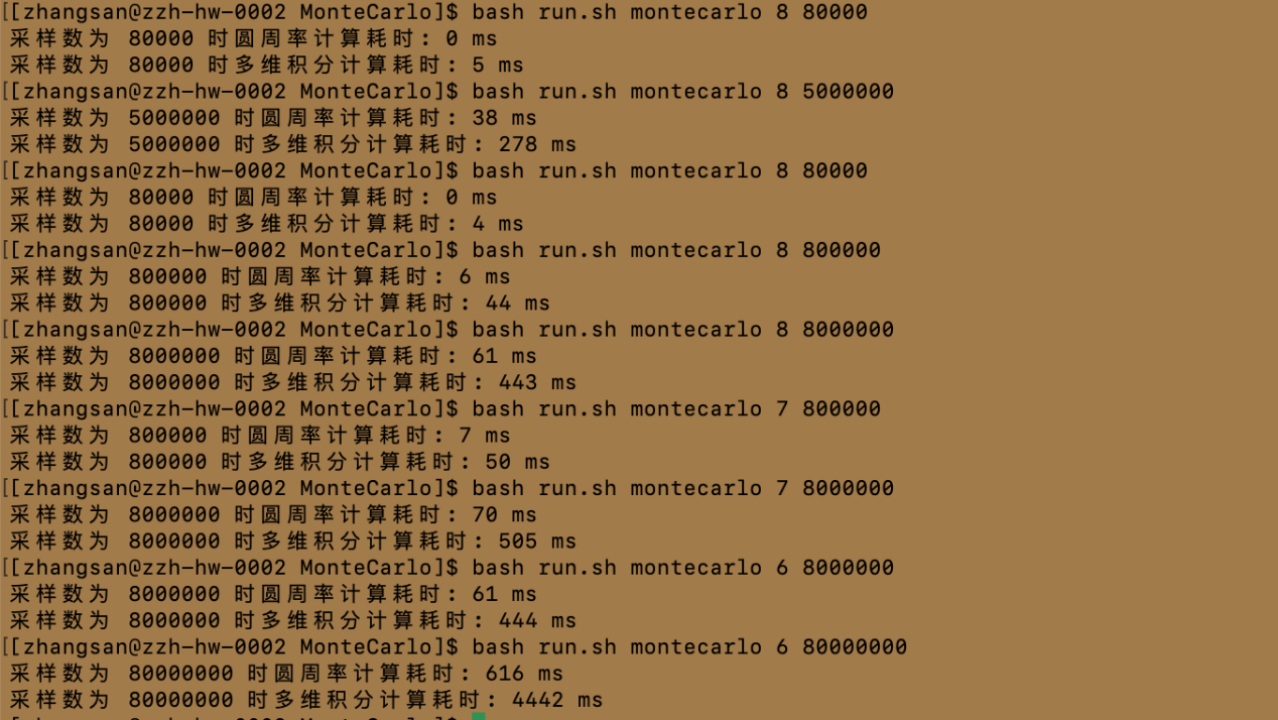
根据上述结果,可以观察到如下现象,并做出对应解释
①随采样数增加,计算耗时增加
我认为这是直观的,因为随着采样数增加,需要进行的计算量也增加,因此计算耗时增加是合理的。
②计算耗时增长不是线性的
因为当采样数增加时,计算耗时的增长速度不是简单的线性关系。例如,当从80000增加到800000时,圆周率计算耗时从0ms增加到6ms,但当从800000增加到8000000时,圆周率计算耗时从6ms增加到61ms。这表明随着采样数的增加,计算耗时的增长速度逐渐减缓。
③多维积分计算耗时更高
与圆周率计算相比,多维积分计算的耗时更高。例如,在相同的采样数下,多维积分计算耗时要比圆周率计算耗时长一个数量级以上。
④增加并行度可以减少计算耗时
可以看到,在某些情况下,增加并行度(如从8到1)可以显著减少计算耗时。这是因为增加并行度可以使得更多的计算任务同时进行,从而提高了计算效率。
保持进程数不变,进一步研究采样点数与运行耗时之间的关系
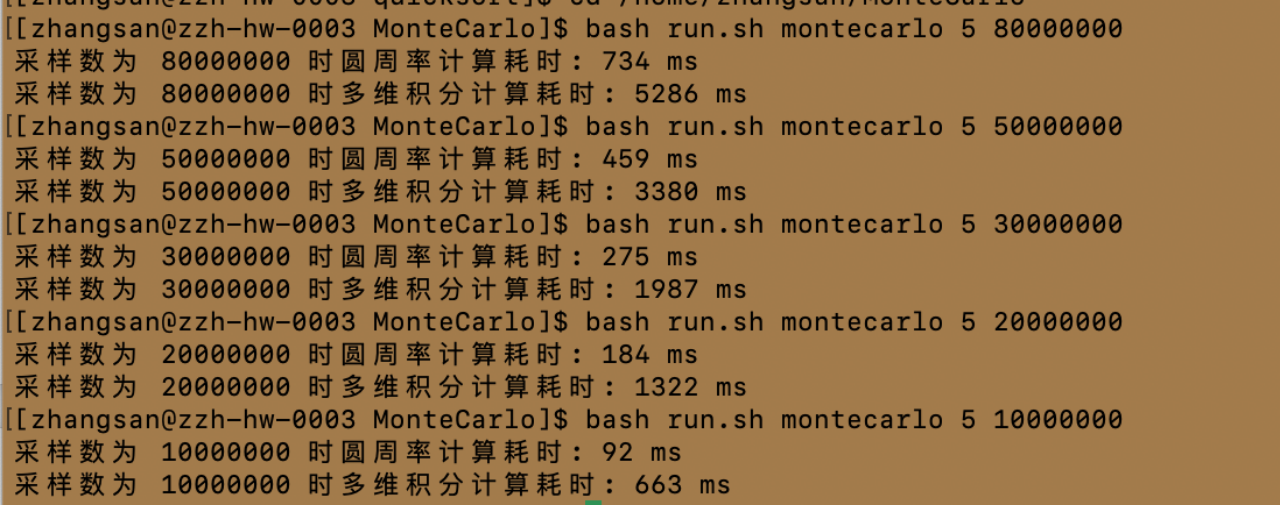
整理出的实验数据如下
| 处理机数量 | 采样点数 | 圆周率计算耗时/ms | 定积分计算耗时/ms |
| 5 | 10000000 | 92 | 663 |
| 5 | 20000000 | 184 | 1322 |
| 5 | 30000000 | 275 | 1987 |
| 5 | 50000000 | 459 | 3380 |
| 5 | 80000000 | 734 | 5286 |
将此部分数据进行可视化,观察其变化规律
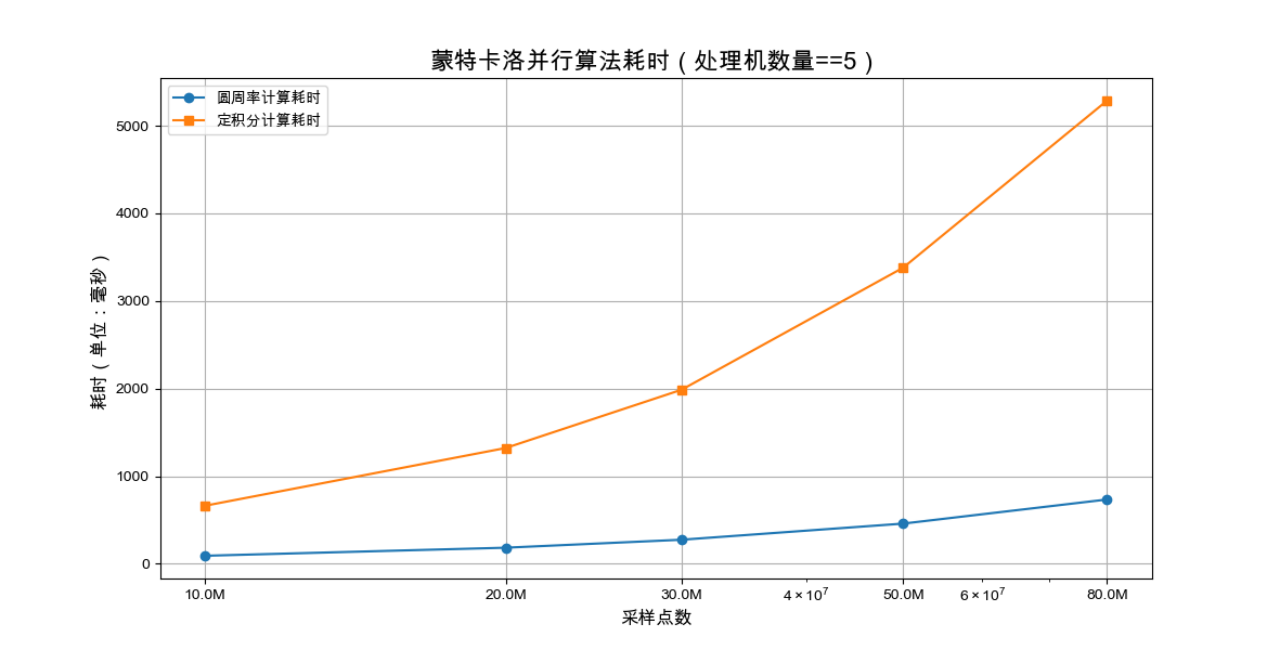
可以看出,当线程数保持不变时,部分区间确实存在一种近似的线性关系。随着采样数的增加,计算耗时也呈现出近似线性增长的趋势。这可能是由于在给定的硬件和软件环境下,随着采样数的增加,计算任务的复杂性增加,导致计算耗时呈线性增长。
五、实验思考与总结
5.1 实验思考
①g++中的-O1、-O2、-O3 的区别是?
在g++编译器中,-O1、-O2和-O3是优化级别的选项,它们指示编译器在编译代码时所采用的优化策略的强度。以下是每个优化级别的简要说明:
-O1:启用基本优化。这是一组较为保守的优化措施,旨在提高程序的执行效率而不增加编译时间。这些优化通常包括消除冗余代码、常量传播、死码删除等。
-O2:进一步优化。这个级别在-O1的基础上增加了更多的优化措施,如循环展开、分支预测、更激进的内联函数等。-O2旨在提供更好的性能,但编译时间会比-O1长。
-O3:最高级别的优化。除了-O2中的优化外,-O3还可能包括进一步的优化技术,如更激进的内联、浮点单位优化等。这个级别可能会增加编译时间,有时也可能引入更多的风险,因为它可能会改变程序的控制流。
每个优化级别都旨在提高程序的性能,但随着优化级别的提高,编译时间也会增加,且程序的调试可能会变得更加困难。通常,选择哪个优化级别取决于程序的性能要求和开发阶段。在开发初期,可能使用较低的优化级别以便于调试;而在发布最终版本时,可能会使用更高的优化级别来提高性能。
②蒙特卡罗算法的并行化原理
蒙特卡罗算法的并行化通过将问题分解为可独立完成的多个子任务,利用随机抽样的独立性,实现在多核处理器、GPU或分布式计算集群上的并行执行。每个计算节点或进程负责一部分抽样和计算工作,减少了通信需求并降低了通信开销。完成所有子任务后,结果被收集并合并,得到最终的统计估计。为了最大化并行效率,合理分配子任务至计算节点以实现负载均衡至关重要。同时,考虑到并行执行中个别节点可能的故障,实现容错机制也是必要的。这种并行化策略显著提高了计算效率,尤其适用于解决需要大量计算资源和时间的复杂系统模拟、风险分析和优化问题,使得在较短时间内完成更多抽样,获得更精确或更可靠的结果成为可能。
5.2 实验总结
在华为鲲鹏云服务器上进行的蒙特卡罗算法实验表明,随着并行进程数量的增加,算法的统计耗时显著减少,验证了并行化策略在提高计算效率方面的有效性。
在实验中,我发现随着采样点数的增加,蒙特卡罗算法的计算耗时相应上升,但这种增长是非线性的。特别是,多维积分任务的耗时远高于圆周率计算,显示出更高计算复杂度。此外,提高并行度能有效减少耗时,因为并行处理允许任务同时执行,提升了计算效率。而在固定进程数下,采样点数与耗时之间的关系近似线性,有助于预测计算时间。
通过这些实验操作,我不仅掌握了蒙特卡罗算法程序的编写和编译运行,还深入理解了并行计算在实际应用中的优势和潜在的优化空间。实验结果强调了合理分配计算资源和优化算法对于提高蒙特卡罗模拟性能的重要性。
END~

早上坏~
偶尔失败,经常偶尔~~