LeetCode刷题之HOT100之数组中的第K个最大元素

2024 6/29 今天天气很好啊，想爬山，奈何下午还有最后的一个汇报。做个题先

1、题目描述

在这里插入图片描述

2、算法分析

看到这个题我想到的就是:

  public int findKthLargest(int[] nums, int k) {Arrays.sort(nums);return nums[nums.length - k ];}

哈哈，我提交上去击败了67.49%，想点正规的算法。
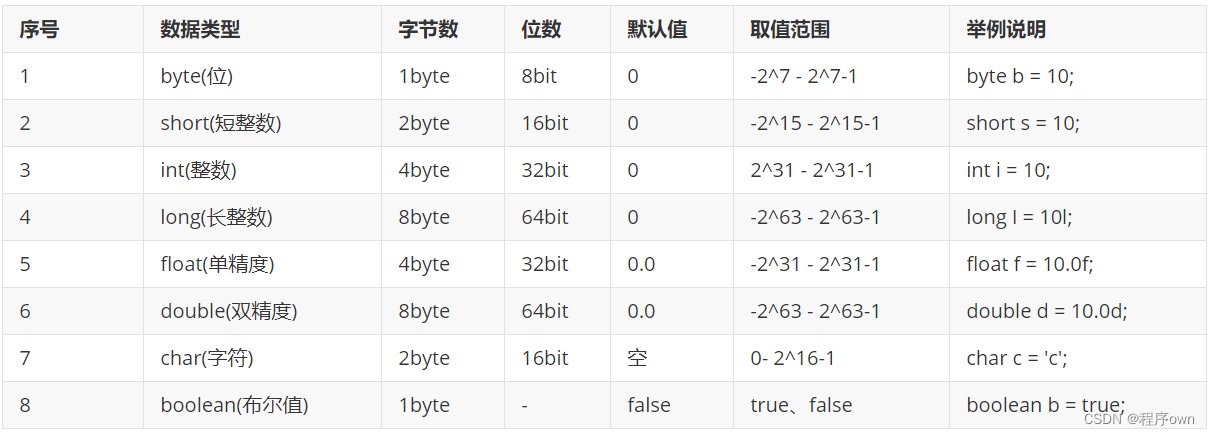
这个是在考察排序的，下图为八大排序复杂度情况。
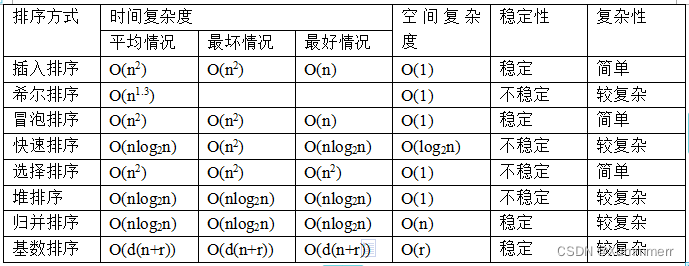
在这里插入图片描述
为了将复杂度控制在O(n)层级。what should i do？那就是在快排的基础上稍作改进：
这里是快排：

3、代码

public int quickSort(int[] nums, int left, int rigth, int k){if(left == rigth){return nums[k];}int base = nums[left];while(left < rigth){while(left < rigth && nums[rigth] > base){rigth--;}while(left < rigth && nums[left] < base){left++;}if(left < rigth){int temp = nums[left];nums[left] = nums[rigth];nums[rigth] = temp;}}if(k <= rigth){return quickSort(nums, left, rigth, k);}else{return quickSort(nums, left + 1, rigth, k);}}public int findKthLargest(int[] nums, int k) {int n = nums.length;return quickSort(nums, 0, n - 1, k);}

测试时间超出限制，所以需要改进一下：

public int quickSort(int[] nums, int left, int rigth, int k){// 当左边界等于右边界时，说明搜索区间只有一个元素，直接返回该元素if(left == rigth){return nums[k];}// 选择基准值（这里我们简单选择左边界的元素作为基准）int base = nums[left], i = left - 1, j = rigth + 1;while (i < j) {// 使用do-while循环进行快速选择的分区过程  // 将小于基准的元素放到左边，大于基准的元素放到右边// 从左向右扫描，找到第一个大于或等于基准的元素  do i++; while (nums[i] < base);// 从右向左扫描，找到第一个小于或等于基准的元素 do j--; while (nums[j] > base);// 如果i和j还未相遇，则交换它们if (i < j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}}// j 现在指向小于基准值的最后一个元素的右边一个位置  // 如果 k 的值小于或等于这个位置（即 k 指向的元素在基准值的左边或与其相等），  // 则第k大的元素在左半部分，递归搜索左半部分 if (k <= j) return quickSort(nums, left, j, k);// 否则，第k大的元素在右半部分，递归搜索右半部分  // 注意：k的值不需要改变，因为我们是基于当前搜索范围的索引来搜索的else return quickSort(nums, j + 1, rigth, k);}public int findKthLargest(int[] nums, int k) {int n = nums.length;return quickSort(nums, 0, n - 1, n - k );}