文章目录
- P、NP、NP-hard 和 NPC
- 多项式时间
- 概念区分
- NP-hard 的证明
- 扩展 NP-hard 问题
- 3-SAT 问题
- TSP 旅行商问题
- Load Balancing
- Load Balancing
- Load balancing on 2 machines is NP-hard
- Load Balancing: List Scheduling
- Load balancing: list scheduling analysis
- Load balancing: LPT rule
- Center selection
- Center selection problem
- Greedy algorithm: a false start
- Center Selection: Greedy Algorithm
- Analysis of Greedy Algorithm
- pricing method:Weighted vertex cover
- Weighted vertex cover 最小权顶点覆盖
- Pricing method 定价法
- 定价法近似算法
- 定价法近似算法例子
- 定价法近似算法分析
- LP rounding: weighted vertex cover
- weighted vertex cover
- Weighted vertex cover: ILP formulation
- LP 可行域
- Poly-time reductions
- Reduction
- Independent set
- Vertex cover
- Vertex cover and independent set reduce to one another
- Set-Cover 集合覆盖
- Vertex cover reduces to set cover
- Satisfiability
- 3-satisfiability reduces to independent set
- Review
- Hamilton
- Hamilton cycle
- Directed Hamilton cycle reduces to Hamilton cycle
- 3-satisfiability reduces to directed Hamilton cycle
近似算法-徐小华
P、NP、NP-hard 和 NPC
多项式时间
多项式时间是指 一个问题的计算时间随着问题的规模增加而增加的速度,多项式时间的算法可以用多项式倍数来表示。
多项式时间的一般形式是 O ( n k ) O(n^k) O(nk),其中 n n n 是问题的规模, k k k 是一个常数。
- 当 k=0 时, O ( n k ) O(n^k) O(nk) 就是 O(1);
- 当 k=1 时, O ( n k ) O(n^k) O(nk) 就是 O(n)。
所以,O(1) 和 O(n) 都是多项式时间的特例。
举例来说,如果一个问题的计算时间是 O ( n 2 ) O(n^2) O(n2),
- 那么当问题的规模 n n n 从 10 增加到 20 时,计算时间会从 100 增加到 400,增加了 4 倍。
- 如果问题的规模再增加 10 倍,变成 200,那么计算时间会变成 40000,增加了 100 倍。
多项式时间的算法通常被认为是高效的,因为它们的运行时间随着问题规模的增长不会太快。相比之下,指数时间、阶乘时间等非多项式时间的算法就很低效,因为它们的运行时间随着问题规模的增长会呈指数爆炸。
多项式时间的算法可以根据它们的 多项式次数 来分类,例如 O(1)、O(log n)、O(n)、O(n log n)、 O ( n 2 ) O(n^2) O(n2)、 O ( n 3 ) O(n^3) O(n3) 等。一般来说,多项式次数越低,算法的效率越高。
下面是一些常见的多项式时间算法的例子:
- O(1):常数时间,指算法的运行时间与问题的规模无关,例如判断一个数是否是偶数、返回数组的第一个元素等。
- O(log n):对数时间,指算法的运行时间与问题的规模的对数成正比,例如二分查找、快速幂等。
- O(n):线性时间,指算法的运行时间与问题的规模成正比,例如遍历数组、线性搜索、计数排序等。
- O(n log n):指算法的运行时间与问题的规模和对数的乘积成正比,例如归并排序、快速排序、堆排序等。
- O ( n 2 ) O(n^2) O(n2):指算法的运行时间与问题的规模的平方成正比,例如冒泡排序、选择排序、插入排序等。
- O ( n 3 ) O(n^3) O(n3):指算法的运行时间与问题的规模的立方成正比,例如矩阵乘法、高斯消元、弗洛伊德算法等。
概念区分
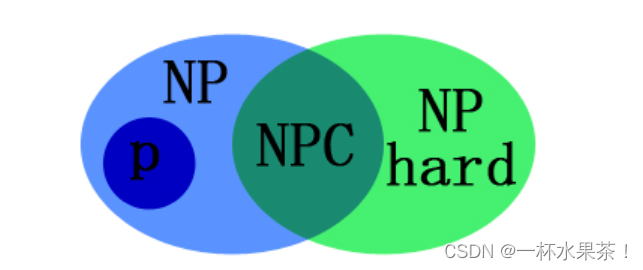
直观:
-
P P P ≈ 可以用多项式时间的确定性算法求解 的问题;
例如,排序、最短路径、二分查找等。
多项式时间意味着,问题的规模(如输入的长度)增大时,算法的运行时间不会超过某个多项式函数的值。
-
N P NP NP ≈ 可以在多项式时间内验证一个解是否正确 的问题。(NP:Nondeterministic polynominal,非确定性多项式)
例如,旅行商问题、哈密顿回路问题、子集和问题等。
不知道这个问题存不存在一个多项式时间的算法,所以叫非确定性(non-deterministic),但是可以 在多项式时间内验证并得出这个问题的一个正确解。
P 类问题是 NP 类问题的子集(即存在多项式时间算法的问题,总能在多项式时间内验证它)。
P P P 问题和 N P NP NP 问题之间的区别: N P NP NP 类问题可以用多项式时间的非确定性算法求解,但是不能用多项式时间的确定性算法求解,而 P P P 类问题可以用多项式时间的确定性算法求解。
-
NP-hard :指 比所有的 N P NP NP 问题都难的问题,即所有的 N P NP NP 问题都可以在多项式时间内约化到它,但它不一定是一个 N P NP NP 问题。
例如,判定停机问题、最长公共子序列问题等。
为了证明 NP = P,想到的方法之一是问题的约化。可以用问题 B 的算法来解决 A ,我们就说问题 A 可以约化成问题 B。比如,二元一次方程的求解可以约化成一元一次方程的求解。
约化是具有传递性的,如 A 约化到 B,B 约化到 C,A 就可以约化到 C,同时不断约化下去,一定会存在一个最大的问题,只需要解决了这个问题,那其下的所有问题也就解决啦!这就是 NPC 概念。
-
NP-complete 问题:属于 NP 问题,且属于 NP-hard 问题。
例如,3SAT 问题、背包问题、图着色问题等。
存在这样一个 NP 问题,所有的 NP 问题都可以约化成它。也就是说,它是 NP 问题中最难的问题,如果能找到一个 NP-complete 问题的多项式时间算法,那么所有的 NP 问题都可以在多项式时间内解决。
P 和 NP 问题的关系是一个未解决的数学难题,目前没有人能证明或否定 P 是否等于 NP。
- 如果
P=NP,那么就意味着所有可以快速验证的问题也可以快速求解,这将对数学、计算机科学、密码学等领域产生巨大的影响。 - 如果
P≠NP,那么就意味着存在一些困难的问题,即使有最强大的计算机也无法在合理的时间内解决。

NP-hard 的证明
证明某个问题是 NP−hard 问题 的一般方法是使用 归约,即 将一个已知的 NP−hard 问题转化为目标问题,从而说明目标问题的难度不低于已知问题。
具体步骤如下:
- 首先,选择一个已知的 NP−hard 问题,例如 3SAT、旅行商问题、哈密顿回路问题、背包问题等。
- 然后,设计一个多项式时间的算法,将已知问题的任意一个实例转化为目标问题的一个实例,使得两个实例的解之间有 一一对应的关系。
- 最后,证明这个转化算法的正确性和有效性,即如果目标问题有一个多项式时间的算法,那么已知问题也有一个多项式时间的算法,这与 NP−hard 问题的定义相矛盾。
关键点:多项式归约( X ≤ P Y X \ ≤_P \ Y X ≤P Y,若 X X X 是 NP-hard,那么 Y Y Y 也是 NP-hard)
例题 1 证明 T S P TSP TSP 问题是 N P − h a r d NP-hard NP−hard 问题 。
证明思路——将 哈密尔顿回路问题 多项式时间归约到 TSP。
- TSP 问题是指给定一系列城市和每对城市之间的距离,求解 经过每一座城市一次并回到起始城市的最短回路。
- 哈密顿回路问题是指给定一个无向图,判断是否存在一条 经过每个顶点一次并回到起点的回路。
证明如下:
1)构造实例:
给定无权图 G = ( V , E ) G = (V,E) G=(V,E) ,构造一个带权完全图 G ’ = ( V , E , W ) G’ = (V,E, W) G’=(V,E,W)
W u v = { 1 , ( u , v ) ∈ E ∞ , ( u , v ) ∉ E W_{uv}=\begin{cases} 1, & (u,v)\in E \\ \infty, & (u,v) \notin E \end{cases} Wuv={1,∞,(u,v)∈E(u,v)∈/E
-
对于图 G G G 中的每对顶点之间的边,将它们的距离设置为 1;
-
对于图 G G G 中不存在的边,将它们的距离设置为一个非常大的值,保证旅行商不会选择这些边。
将 TSP 的目标函数设置为 最小化旅行的总路程。
2)证明等价性:
这样一来,如果 图 G G G 存在一个哈密尔顿回路,那么 相应的 TSP 实例也存在一个路程等于图 G G G 中哈密尔顿回路长度的最优解。
反过来,如果 TSP 实例存在一个最优解, 它对应的路径将经过每个城市一次,并且总路程等于哈密尔顿回路长度,因此图 G G G 存在一 个哈密尔顿回路。
综上,由于哈密尔顿回路问题是一个 已知的 NP-hard 问题,上述归约证明了 TSP 是 NP-hard 问题。
例题 2 证明最大加权独立集问题是 N P − h a r d NP-hard NP−hard 问题。
证明思路——从 最大独立集问题 多项式归约到 最大加权独立集问题。
- 最大独立集问题:给定一个无向图 G G G 和一个正整数 k k k,问题是 找到 G G G 中具有最大独立集大小的一个独立集(即,其中没有两个顶点相邻),该独立集的大小至少为 k k k。
- 最大加权独立集问题:给定一个带有权重的无向图 G G G 和一个正整数 k k k,问题是找到 G G G 中具有最大权重的独立集,该独立集的大小至少为 k k k。
证明如下:
1)构造实例:
对于给定的最大独立集问题实例(图 G = ( V , E ) G = (V,E) G=(V,E) 和正整数 k k k),构造一个具有相同顶点集的带权重的图 G ’ = ( V , E , W ) G’ = (V,E, W) G’=(V,E,W),对于任何 v ∈ V v \in V v∈V , w ( v ) = 1 w(v) = 1 w(v)=1。对于 G G G 中的每条边 ( u , v ) (u, v) (u,v), 在 G ′ G' G′ 中添加一条带有权重 0 的边 ( u , v ) (u, v) (u,v),保持 k k k 不变。
2)证明等价性:
如果 G G G 中存在一个大小至少为 k k k 的独立集,那么在 G ′ G' G′ 中的相应顶点集也是 一个大小至少为 k k k 的独立集,因为 G ′ G' G′ 中的新添加的边都具有权重 0。
如果 G ′ G' G′ 中存在一个大小至少为 k k k 的独立集,那么在 G G G 中的相应顶点集也是一个大小至少为 k k k 的独立集,因为 G ′ G' G′ 中的边都具有权重 0,所以在计算最大权重时,只有顶点的数量起作用。
由于最大独立集问题是一个已知的 NP-hard 问题,上述归约证明了最大加权独立集也是一个 NP-hard 问题。
扩展 NP-hard 问题
3-SAT 问题
对于任意的布尔表达式总能写成以下标准式: ( . . ∨ . . ∨ . . ) ∧ ( . . ∨ . . ∨ . . ) ∧ ( . . ∨ . . ∨ . . ) (.. \vee .. \vee ..)\ \wedge \ (.. \vee .. \vee ..)\ \wedge (.. \vee .. \vee ..) (..∨..∨..) ∧ (..∨..∨..) ∧(..∨..∨..),很多个与 ∧ \wedge ∧ 并在一起,每一个 ( . . ∨ . . ∨ . . ) (.. \vee .. \vee ..) (..∨..∨..) 都是一个 Clause。3-SAT 问题,每个 Clause 子句恰好都有 3 个元素。
TSP 旅行商问题
TSP 是 Travelling Salesman Problem 的缩写,中文翻译成旅行商问题。
给定一系列城市和每对城市之间的距离,求解经过每一座城市一次并回到起始城市的最短回路。
Load Balancing
Load Balancing
输入: m m m 台相同的机器; n ≥ m n ≥ m n≥m 个作业,作业 j j j 的处理时间为 t j t_j tj。
-
作业 j j j 必须在一台机器上连续运行。
-
一台机器一次最多可以处理一个作业。
定义:设 S ( i ) S(i) S(i) 是分配给机器 i i i 的作业集,则机器 i i i 的 负载 为 L i = ∑ j ∈ S ( i ) t j L_i= \displaystyle \sum_{j \in S(i)}t_j Li=j∈S(i)∑tj
定义:makespan 是 任何机器上的最大负载 L = m a x i L i L=max_i L_i L=maxiLi
负载均衡:将每个作业分配给机器,以 最小化 makespan。

Load balancing on 2 machines is NP-hard
Claim. Load balancing is hard even if m = 2 machines.
Pf. PARTITION ≤ P ≤_P ≤P LOAD-BALANCE.
≤ P ≤_P ≤P 的理解:负载均衡 比 分区问题 还要难。
想表达啥呢?
- 就是想说 负载均衡是 NP-hard 问题。
分区问题(Partition problem)目的是把一个多重集 S S S 分为 S 1 S_1 S1 和 S 2 S_2 S2 两个子集,要求 S 1 S_1 S1 和 S 2 S_2 S2 这两个集合中所有数的和相等。
分区问题属于 NPC 问题。
实例:现有多重集 S = { 3 , 1 , 1 , 2 , 2 , 1 } S=\{3,1,1,2,2,1 \} S={3,1,1,2,2,1} ,可以被分为 S 1 = { 1 , 1 , 1 , 2 } S_1=\{1,1,1,2\} S1={1,1,1,2} 以及 S 2 = { 2 , 3 } S_2=\{2,3\} S2={2,3},两者元素之和皆为 5。
三分区问题与分区问题有很大不同,三分区问题要求每个子集中都有 3 个元素。三分区问题比分区问题更难。
Load Balancing: List Scheduling
List-scheduling algorithm. 考虑按某种固定顺序的 n n n个作业,将作业 j j j 分配给到目前为止负载最小的机器。

实现: L [ k ] L[k] L[k] 使用优先队列,时间复杂度为 O ( n l o g m ) O(n log m) O(nlogm)。

Load balancing: list scheduling analysis
引理 1:最优 makespan L ∗ ≥ m a x j t j L^* ≥ max_jt_j L∗≥maxjtj
证明:一定有一台机器需要处理最耗时的工作。
引理 2:最优 makespan L ∗ ≥ 1 m ∑ j t j L^* ≥ \frac{1}{m} \displaystyle \sum_j t_j L∗≥m1j∑tj
证明:
-
总处理时间为 ∑ k t k \displaystyle \sum_k t_k k∑tk。
-
m m m 台机器中的一台必须至少完成全部工作的 1 / m 1/m 1/m。
定理:贪心算法是 2-近似 算法。
证明:考虑瓶颈机器 i i i 的负载 L [ i ] L[i] L[i],瓶颈机器即 最终负载最高的机器。
让 j j j 是机器 i i i 上安排的最后一个作业,当工作 j j j 分配给机器 i i i 时, i i i 的负载最小,其分配前的负载为 L [ i ] – t j L[i]–t_j L[i]–tj;
因此对于所有 1 ≤ k ≤ m 1≤k≤m 1≤k≤m, L [ i ] – t j ≤ L [ k ] L[i]–t_j≤L[k] L[i]–tj≤L[k]。
对所有 k k k 上的不等式求和,两边再除以 m m m,得
L [ i ] − t j ≤ 1 m ∑ k L [ k ] = 1 m ∑ k t k ≤ L ∗ L[i] - t_j ≤ \frac{1}{m} \displaystyle \sum_k L[k] = \frac{1}{m} \displaystyle \sum_k t_k ≤ L^* L[i]−tj≤m1k∑L[k]=m1k∑tk≤L∗
其中, 1 m ∑ k t k ≤ L ∗ \frac{1}{m} \displaystyle \sum_k t_k ≤ L^* m1k∑tk≤L∗ 应用引理 2,至此, L [ i ] − t j ≤ L ∗ L[i] - t_j ≤ L^* L[i]−tj≤L∗ 成立。
由引理 1, t j ≤ L ∗ t_j ≤ L^* tj≤L∗ 。
因此, L = L [ i ] = ( L [ i ] − t j ) + t j ≤ 2 L ∗ L = L[i] = (L[i] - t_j) + t_j ≤ 2L^* L=L[i]=(L[i]−tj)+tj≤2L∗,即贪心算法是 2-近似 算法。
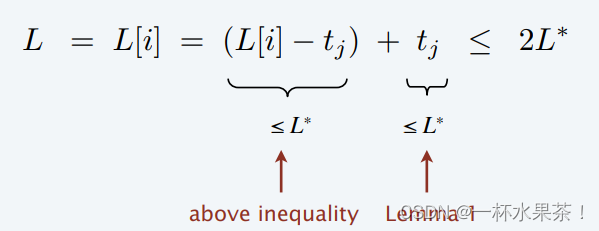
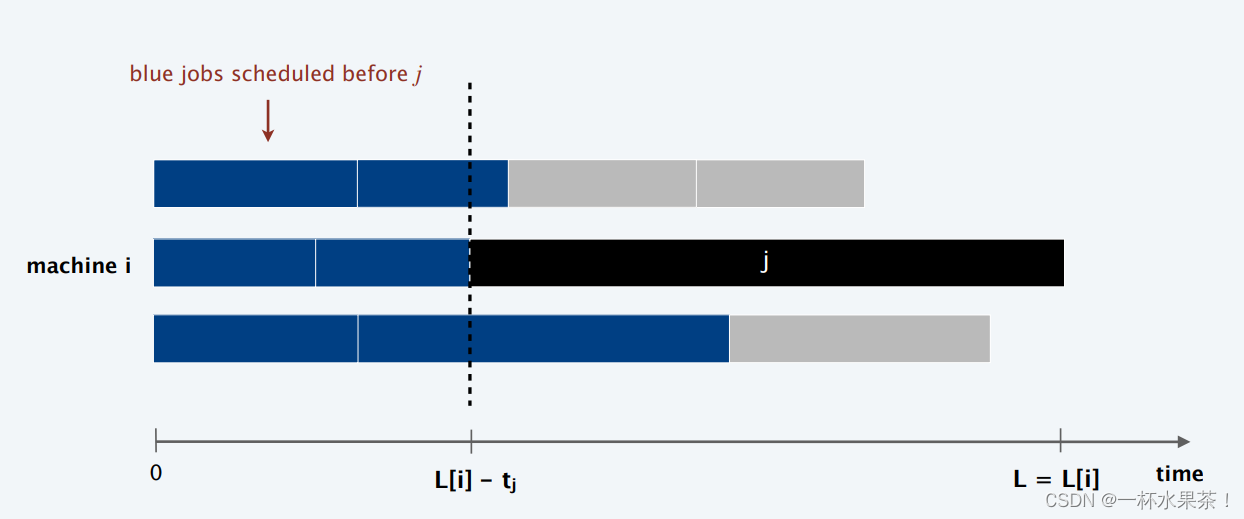
举个例子: m m m 台机器,前 m ( m − 1 ) m(m-1) m(m−1) 个作业的长度为 1,最后一个作业长度为 m m m。

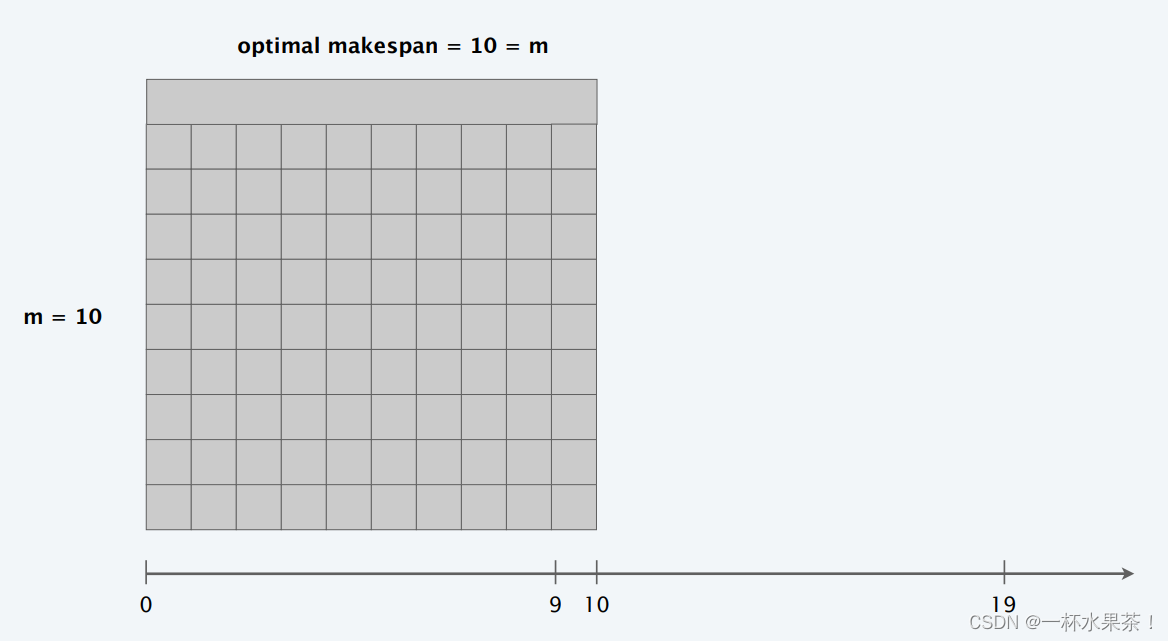
可知, L = 2 m − 1 L = 2m-1 L=2m−1 ≤ 2 L ∗ = 2 m 2L^* = 2m 2L∗=2m。
Load balancing: LPT rule
Longest processing time (LPT). 按处理时间的降序对 n n n 个作业进行排序;然后运行 列表调度算法。

观察:如果瓶颈机器 i i i 只有 1 个作业,那么是最优的。
证明:任何解决方案都必须安排这个作业。
引理 3:如果有多于 m m m 个作业, L ∗ ≥ 2 t m + 1 L^* ≥ 2 t_{m+1} L∗≥2tm+1。
证明:考虑前 m + 1 m+1 m+1 个作业的处理时间, t 1 ≥ t 2 ≥ . . . ≥ t m + 1 t_1 ≥ t_2 ≥ ... ≥ t_{m+1} t1≥t2≥...≥tm+1,作业按处理时间降序排列,所以这前 m + 1 m+1 m+1 的每个作业至少消耗 t m + 1 t_{m+1} tm+1 时间,
m + 1 m+1 m+1 个作业和 m m m 台机器,由鸽巢原理,至少有一台机器被分配两个作业,即 L ∗ ≥ 2 t m + 1 L^* ≥ 2 t_{m+1} L∗≥2tm+1。
定理:LPT rule 是一个 3 2 \frac{3}{2} 23-近似 算法。
证明:(类似于列表调度的证明)
考虑瓶颈机器 i i i 的负载 L [ i ] L[i] L[i],让 j j j 是机器 i i i 上安排的最后一个作业,
假设机器 i i i 至少被分配两个作业,那么 j ≥ m + 1 j ≥ m+1 j≥m+1,作业按处理时间降序排列,所以 t j ≤ t m + 1 t_j ≤ t_{m+1} tj≤tm+1,
由引理 3, t m + 1 ≤ 1 2 L ∗ t_{m+1} ≤ \frac{1}{2}L^* tm+1≤21L∗,所以 t j ≤ 1 2 L ∗ t_j ≤ \frac{1}{2}L^* tj≤21L∗,那么
L = L [ i ] = ( L [ i ] − t j ) + t j ≤ 3 2 L ∗ L = L[i] = (L[i] - t_j) + t_j ≤ \frac{3}{2} L^* L=L[i]=(L[i]−tj)+tj≤23L∗
这里 L [ i ] − t j ≤ L ∗ L[i] - t_j ≤ L^* L[i]−tj≤L∗ 同列表调度的证明。
定理:LPT rule 是一个 4 3 \frac{4}{3} 34-近似 算法。
证明:对相同算法进行更复杂的分析。
举个例子: m m m 台机器, n = 2 m + 1 n = 2m+1 n=2m+1 个作业,2 个长度为 m , m + 1 , … , 2 m – 1 m, m+1, … , 2m–1 m,m+1,…,2m–1 的作业和一个长度为 m m m 的作业,则 L / L ∗ = ( 4 m − 1 ) / ( 3 m ) L / L^* = (4m − 1) / (3m) L/L∗=(4m−1)/(3m)
Center selection
Center selection problem
Input. Set of n sites s 1 , … , s n s_1,…,s_n s1,…,sn and an integer k > 0 k > 0 k>0.
在给定一些 site 的位置后,找到一组中心的位置,使得 每个 site 都在某个中心的覆盖范围内,且覆盖半径尽可能小。覆盖半径是指 site 到最近的中心的距离的最大值。
目标:求 使覆盖半径 r ( C ) r(C) r(C) 最小化的中心集 C C C,使得 ∣ C ∣ = k |C|=k ∣C∣=k。
为了理解 Center selection ,举个例子,下图是 k = 4 k=4 k=4 时的 Center selection 图示:
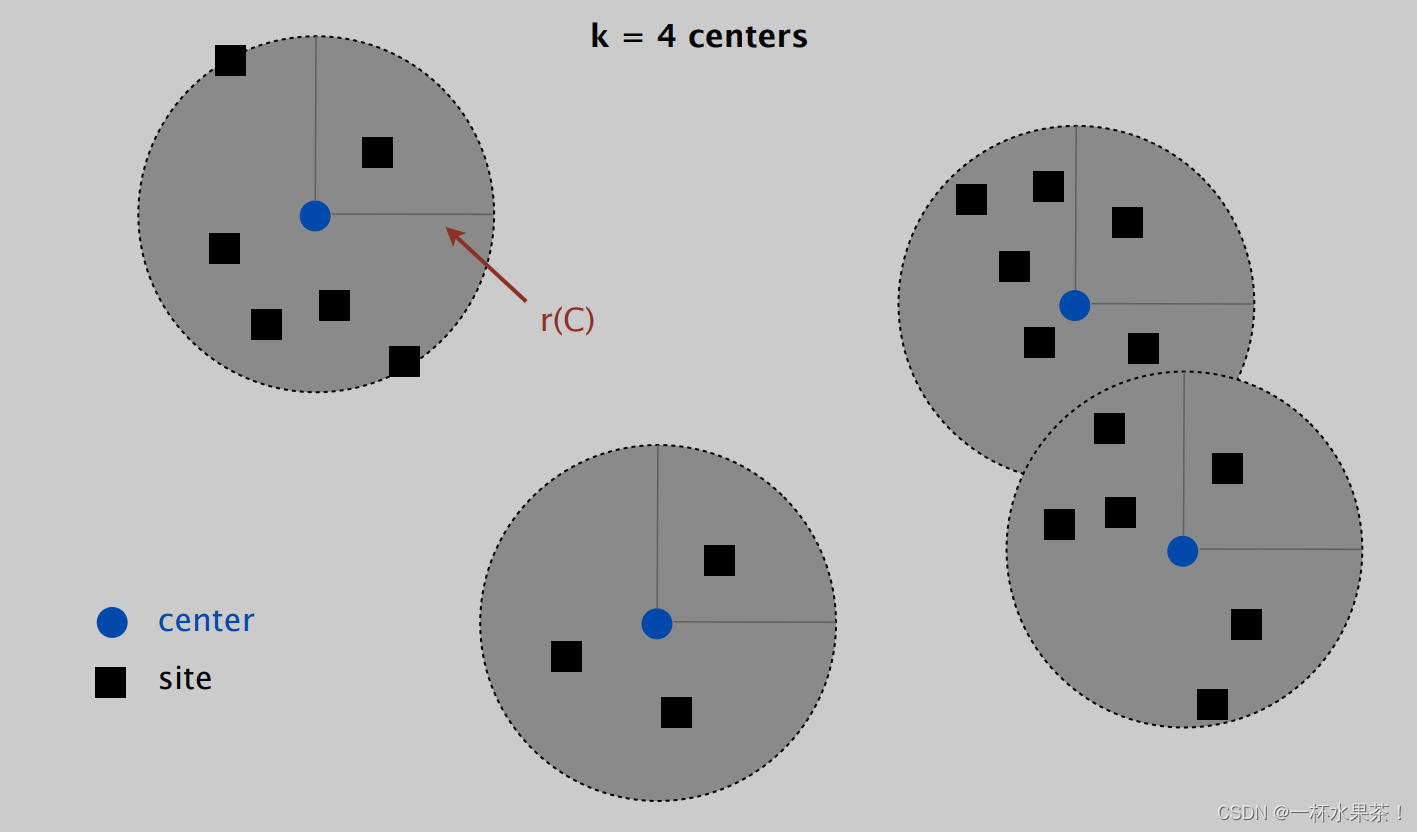
- d i s t ( x , y ) dist(x, y) dist(x,y) = distance between sites x x x and y y y.
- d i s t ( s i , C ) = m i n c ∈ C d i s t ( s i , c ) dist(s_i , C) = min_{c ∈ C} dist(s_i , c) dist(si,C)=minc∈Cdist(si,c) = distance from s i s_i si to closest center.
- r ( C ) = m a x i d i s t ( s i , C ) r(C) = max_i dist(s_i , C) r(C)=maxidist(si,C) = smallest covering radius.
- d i s t ( x , y ) dist(x, y) dist(x,y) 就是 site x x x 和 site y y y 之间的距离。
- d i s t ( s i , C ) dist(s_i , C) dist(si,C) 就是 site s i s_i si 离最近中心的距离,比如下图中 黄绿色箭头 有两条,但是选到下面那个圆心的那条。
- r ( C ) r(C) r(C) 就是 所有 site 和最近中心的距离的最大值,如图中浅蓝色线所示。在 所有的 Center (图中的圆圈区域)中,必定存在至少一个 site 在圆上,和中心的距离为 r ( C ) r(C) r(C),这是所有的 Center 中离最近的中心最远的 site。
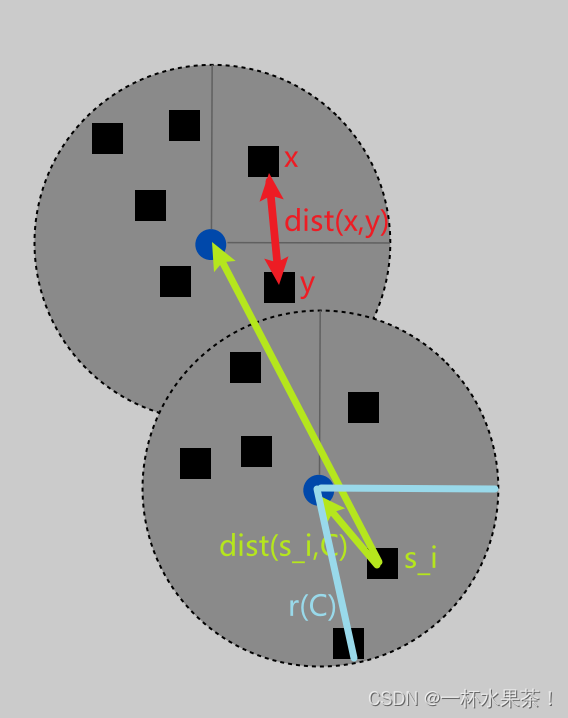

当 k = 4 k=4 k=4 时,有 Center 1, 2, 3, 4 四个 Center,其中 Center 1 中的 s 1 s_1 s1 和 s 2 s_2 s2 距离最近的中心 C 1 C_1 C1 的距离为 r ( C ) r(C) r(C),这是 所有的 site 和其最近的中心的距离中的最大值。可以看到 Center 2 中不存在 site 距离最近中心 C 2 C_2 C2 的距离等于 r ( C ) r(C) r(C)。
所以,Center selection problem 就是,把所有 site 划分为 k k k 个 Center,求 r ( C ) r(C) r(C) 的最小值。
- d i s t ( x , x ) = 0 dist(x, x) = 0 dist(x,x)=0
- d i s t ( x , y ) = d i s t ( y , x ) dist(x, y) = dist(y, x) dist(x,y)=dist(y,x)
- 三角不等式: d i s t ( x , y ) ≤ d i s t ( x , z ) + d i s t ( z , y ) dist(x, y) ≤ dist(x, z) + dist(z, y) dist(x,y)≤dist(x,z)+dist(z,y)
其中,每个 site 是平面中的一个点,Center 中心可以是平面中任何一个点(不一定在 site 中选择), d i s t ( x , y ) dist(x,y) dist(x,y)=欧几里得距离。
Greedy algorithm: a false start
Greedy algorithm.
-
将第一个中心放在 单个中心的最佳位置,即 site 的位置的平均值。这样可以保证第一个中心的覆盖半径是最小的。
-
然后 不断添加中心,以尽可能 减少每次的覆盖半径。
注意:该算法中,Center 中心可以是平面中任何一个点(不一定在 site 中选择)。
比如,当 k = 2 k=2 k=2 时,选择的第一个中心如下图:

Greedy Center 1 是第一个中心,它是 单个中心的最佳位置。
但是很明显这个中心不是 k = 2 k=2 k=2 时的最优解,最优解应像下图绿色的两个圆,两个 Center 分别是两个圆的圆心。

Center Selection: Greedy Algorithm
Greedy algorithm. 反复选择 离任何现有中心最远的 site 作为下一个中心。
这是为了尽可能地将 site 分散到不同的中心,从而减少每个中心的覆盖半径。
注意:该算法中,Center 中心必须在 site 中选择。
当 k = 1 k=1 k=1 时,即 第一个中心 Center,随机 从所有 site 中选择。

Property. 在终止时, C C C 中的所有中心成对地相距至少 r ( C ) r(C) r(C)。
反证法:假设有两个中心,按照算法,第二个中心是距离第一个中心最远的 site。 r ( C ) r(C) r(C) 是所有 site 中离最近中心的最远距离,如果两中心距离小于 r ( C ) r(C) r(C),即 第二个中心距离第一个中心小于 r ( C ) r(C) r(C),那么 余下的 site 距离第一个中心都小于 r ( C ) r(C) r(C),所以所有 site 都可以被第一个中心覆盖(画图容易理解),从而可以删除第二个中心。
这个算法的运行时间是 O ( n k ) O(nk) O(nk),
- 因为每次选择新的中心需要遍历所有的点,计算它们到已有中心的距离,然后找出最大的一个。
- 这个过程需要重复 k k k 次,所以总的时间复杂度是 O ( n k ) O(nk) O(nk)。
如果 k k k 是一个常数,那么这个算法的运行时间就是 O ( n ) O(n) O(n)。
Analysis of Greedy Algorithm

定理:假设 C ∗ C^* C∗ 是最优的一组中心,那么 r ( C ) ≤ 2 r ( C ∗ ) r(C) ≤ 2r(C^*) r(C)≤2r(C∗)。
【思路】
C ∗ C^* C∗ 中的每个 site c i ∗ c_i^* ci∗,是 假设的最优的一组中心,也就是说,它的覆盖半径 r ( C ∗ ) r(C^*) r(C∗) 是所有可能的一组中心中最小的。对于 C ∗ C^* C∗ 中的任何 site s s s,它到 C ∗ C^* C∗ 中的最近的中心 c i ∗ c_i^* ci∗ 的距离都不会超过 r ( C ∗ ) r(C^*) r(C∗)。
C C C 中的每个 site c i c_i ci,是 贪心算法得到的一组中心。它的覆盖半径 r ( C ) > r ( C ∗ ) r(C) > r(C^*) r(C)>r(C∗)。对于 C C C 中的任何 site s s s,它到 C C C 中的最近的中心 c i c_i ci 的距离都不会超过 r ( C ) r(C) r(C)。
接下来,在 C C C 中的每个 site c i c_i ci 的周围画一个半径为 1 2 r ( C ) \frac{1}{2}r(C) 21r(C) 的球。可以想象,这些球就像是 C C C 中的每个中心的覆盖范围,它们可以覆盖到 一定的 site。我们想要知道,这些球里面有没有 C ∗ C^* C∗ 中的中心,也就是说,有没有 C ∗ C^* C∗ 中的中心距离 C C C 中的中心很近。然后发现,每个球里面正好有一个 C ∗ C^* C∗ 中的中心 c i ∗ c_i^* ci∗,也就是说,每个 c i c_i ci 都有一个最近的 c i ∗ c_i^* ci∗,并且它们的距离小于 1 2 r ( C ) \frac{1}{2}r(C) 21r(C)。
这样,我们就构造了一个与 C C C 对应的一组中心 C ∗ C^* C∗。
证明:
假设 r ( C ∗ ) < 1 2 r ( C ) r(C^*) < \frac{1}{2}r(C) r(C∗)<21r(C),
对于 C C C 中的每个site c i c_i ci,考虑其周围半径为 1 2 r ( C ) \frac{1}{2}r(C) 21r(C) 的球,每个球正好有一个 c i ∗ c_i^* ci∗;
这一步是为了构造一个与 C C C 对应的一组中心 C ∗ C^* C∗,使得每个 c i c_i ci 都有一个最近的 c i ∗ c_i^* ci∗,并且它们的距离小于 1 2 r ( C ) \frac{1}{2}r(C) 21r(C)。
设 c i c_i ci 为与 c i ∗ c^*_i ci∗ 配对的 site,考虑 C ∗ C^* C∗ 中的任何 site s s s 及其最近的中心 c i ∗ c_i^* ci∗,
d i s t ( s , C ) ≤ d i s t ( s , c i ) ≤ d i s t ( s , c i ∗ ) + d i s t ( c i ∗ , c i ) ≤ 2 r ( C ∗ ) dist(s, C) ≤ dist(s, c_i) ≤ dist(s, c_i^*) + dist(c_i^*, c_i) ≤ 2r(C^*) dist(s,C)≤dist(s,ci)≤dist(s,ci∗)+dist(ci∗,ci)≤2r(C∗);
s s s 到 c i c_i ci 的距离可以用 三角不等式 分解为 s s s 到 c i ∗ c_i^* ci∗ 的距离加上 c i ∗ c_i^* ci∗ 到 c i c_i ci 的距离,而这两个距离都不会超过 r ( C ∗ ) r(C^*) r(C∗),因为 c i ∗ c_i^* ci∗ 是 s s s 和 c i c_i ci 最近的中心。
即 r ( C ) ≤ 2 r ( C ∗ ) r(C) ≤ 2r(C^*) r(C)≤2r(C∗),这与假设矛盾,因此 r ( C ∗ ) ≥ 1 2 r ( C ) r(C^*) ≥ \frac{1}{2}r(C) r(C∗)≥21r(C),即 r ( C ) ≤ 2 r ( C ∗ ) r(C) ≤ 2r(C^*) r(C)≤2r(C∗)。
得出结论,即 C C C 的覆盖半径不会超过 C ∗ C^* C∗ 的覆盖半径的两倍。
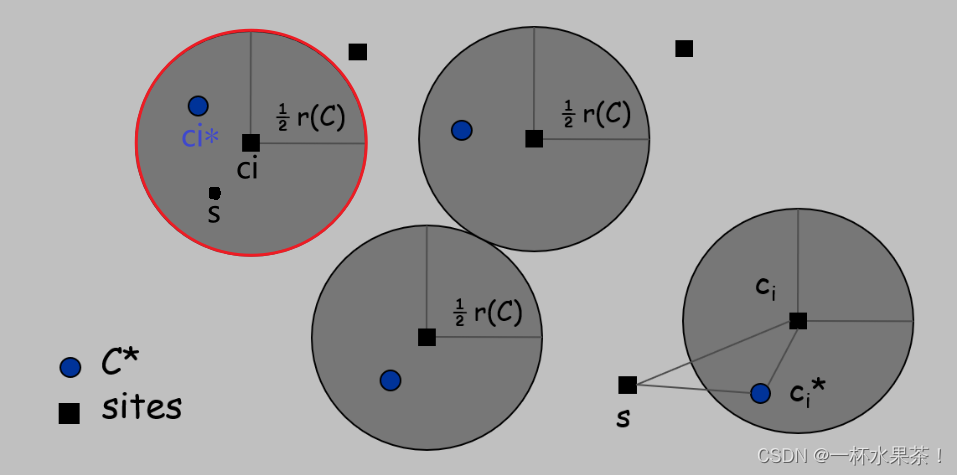
每个球正好有一个 c i ∗ c_i^* ci∗ ?
为什么在 c i c_i ci 周围的每个球 至少有一个 c ∗ c^* c∗ ?
如果一个球里面没有 C ∗ C^* C∗ 中的中心 c ∗ c^* c∗,那么 c i c_i ci 就不在 C ∗ C^* C∗ 中任何中心的 1 2 r ( C ) \frac{1}{2}r(C) 21r(C) 内,这与 r ( C ∗ ) < 1 2 r ( C ) r(C^*)<\frac{1}{2}r(C) r(C∗)<21r(C) 的假设相矛盾。
为什么在 c i c_i ci 周围的每个球 至多有一个 c ∗ c^* c∗ ?
这些 球是不相交的,每个球至少包含一个 c ∗ c^* c∗,并且 ∣ c ∣ = ∣ c ∗ ∣ |c|=|c^*| ∣c∣=∣c∗∣。
- 首先,这些球是 不相交 的,因为它们的半径都是 1 2 r ( C ) \frac{1}{2} r(C) 21r(C),而 C C C 中的所有中心成对地相距至少 r ( C ) r(C) r(C)。这意味着任意两个球的中心之间的距离都大于等于 r ( C ) r(C) r(C),而它们的半径之和都等于 r ( C ) r(C) r(C),所以它们不会重叠。
- 其次,每个球至少包含一个 c i ∗ c_i^* ci∗,这是前面已经证明过的。
- 最后, ∣ c ∣ = ∣ c ∗ ∣ |c|=|c^*| ∣c∣=∣c∗∣,这是 因为 C C C 和 C ∗ C^* C∗ 都是由 k k k 个中心组成的,而且 C ∗ C^* C∗ 是最优的一组中心,所以它不能有多余的中心。这意味着每个 c i ∗ c_i^* ci∗ 都必须被一个球包含,否则它就不会覆盖任何 site,从而导致 r ( C ∗ ) r(C^*) r(C∗) 增大。因此,每个球至多有一个 c i ∗ c_i^* ci∗。
定理:贪心算法是 Center selection problem 的 2-近似 算法。
注意:贪心算法总是将中心放置在 site 上,但仍在 允许在任何位置放置中心的最佳解决方案 的 2 倍以内。
pricing method:Weighted vertex cover
Weighted vertex cover 最小权顶点覆盖
Definition. 给定一个图 G = ( V , E ) G = (V, E) G=(V,E),一个顶点覆盖是一个集合 S ⊆ V S ⊆ V S⊆V,使得 E E E 中的每条边都至少有一端在 S S S 中。
Weighted vertex cover. 给定一个带有顶点权重的图 G G G,找到一个 权重最小的顶点覆盖。

可以理解为,顶点覆盖就是 用顶点去覆盖所有的边。
- 比如,左上角的顶点覆盖了边 Edge 1, 3, 4;右下角的顶点覆盖了边 Edge 2, 3, 5。至此,所有的边均被覆盖。左下角和右上角的顶点没有覆盖任何边。
如果单看一条边,就要满足每条边都至少有一个眼睛可以“保护”。
- 比如,只看 Edge 1,左上角的顶点保护(覆盖)了这条边。
下图顶点覆盖包含 2 个顶点,覆盖了所有的边:
Pricing method 定价法
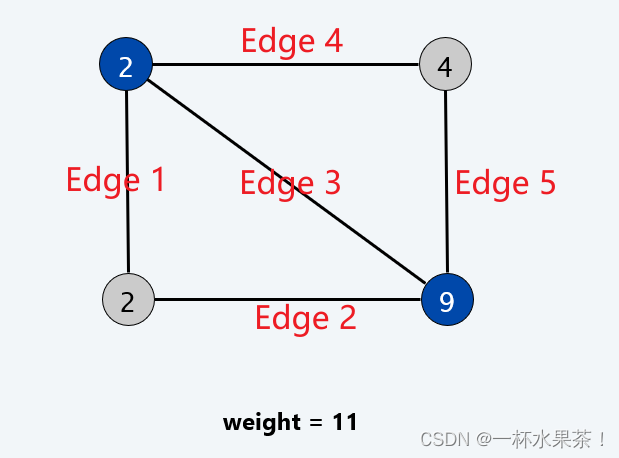
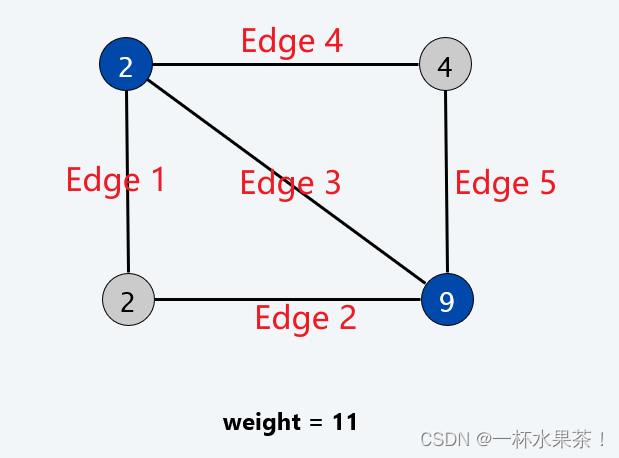
Pricing method. 每条边都必须被某个顶点覆盖。边 e = ( i , j ) e=(i,j) e=(i,j) 为同时使用顶点 i i i 和 j j j 而付出的代价 p e ≥ 0 p_e≥0 pe≥0。
- 把顶点 i i i 的权看作保护费 w i w_i wi,每一条边必须为覆盖它的顶点支付“一份”保护费,即顶点 i i i 覆盖的边一起支付保护费 w i w_i wi。
理解:并不是所有的边都会出钱,因为顶点一旦具备保护(覆盖)能力后,与其相邻的所有边均被保护(覆盖)。
公平性:入射到顶点 i i i 的边应总共付出代价 ≤ w i ≤w_i ≤wi。

- 选择一个顶点 i i i 覆盖所有与 i i i 关联的边,因此要这些边支付总和多于顶点 i i i 的费用是“不公平的”。
- 如果对每一个顶点 i i i,所有与 i i i 关联的边不必支付多于顶点 i i i 的费用,即 ∑ e = ( i , j ) p e ≤ w i \displaystyle \sum_{e=(i,j)} p_e ≤ w_i e=(i,j)∑pe≤wi,则称价格 p e p_e pe 是公平的。
- 如上图所示,对于左上角顶点, E d g e 1 + E d g e 3 + E d g e 4 Edge1+Edge3+Edge4 Edge1+Edge3+Edge4 所支付的费用和 ⩽ 2 \leqslant 2 ⩽2;
- 对于右下角顶点, E d g e 2 + E d g e 3 + E d g e 5 Edge2+Edge3+Edge5 Edge2+Edge3+Edge5 所支付的费用和 ⩽ 9 \leqslant 9 ⩽9。
- 注意,左上角和右下角的顶点所连接的边 E d g e 3 Edge3 Edge3 贡献了两次 p e p_e pe。
每一个顶点 i ∈ V i \in V i∈V 有一个权 w i ≥ 0 w_i≥0 wi≥0,顶点集合 S S S 的权记作 w ( S ) = ∑ i ∈ S w i w(S) =\displaystyle \sum_{i \in S}w_i w(S)=i∈S∑wi。
公平性引理:对于任何顶点覆盖 S S S 和任何公平价格 p e p_e pe, ∑ e ∈ E p e ⩽ w ( S ) \displaystyle \sum_{e \in E} p_e \leqslant w(S) e∈E∑pe⩽w(S)。
证明:
考虑顶点覆盖 S S S,
根据公平性的定义,对每一个顶点 i ∈ S i \in S i∈S, ∑ e = ( i , j ) p e ⩽ w i \displaystyle \sum_{e=(i,j)} p_e \leqslant w_i e=(i,j)∑pe⩽wi ,对 S S S 的所有顶点将这些不等式相加,得到:
∑ i ∈ S ∑ e = ( i , j ) p e ⩽ ∑ i ∈ S w i = w ( S ) \displaystyle \sum_{i \in S} \sum_{e=(i,j)} p_e \leqslant \sum_{i \in S}w_i = w(S) i∈S∑e=(i,j)∑pe⩽i∈S∑wi=w(S)
因为 S S S 是一个顶点覆盖,故每一条边对 ∑ i ∈ S ∑ e = ( i , j ) p e \displaystyle \sum_{i \in S} \sum_{e=(i,j)} p_e i∈S∑e=(i,j)∑pe 至少贡献一个 p e p_e pe,可能贡献两个 p e p_e pe,因为一条边的两个端点可能都在 S S S 中,而价格是非负的,所以
∑ e ∈ E p e ⩽ ∑ i ∈ S ∑ e = ( i , j ) p e \displaystyle \sum_{e\in E}p_e \leqslant \sum_{i \in S}\sum_{e=(i,j)}p_e e∈E∑pe⩽i∈S∑e=(i,j)∑pe
由这两个表达式,得到
∑ e ∈ E p e ⩽ w ( S ) \displaystyle \sum_{e \in E} p_e \leqslant w(S) e∈E∑pe⩽w(S)
可证。
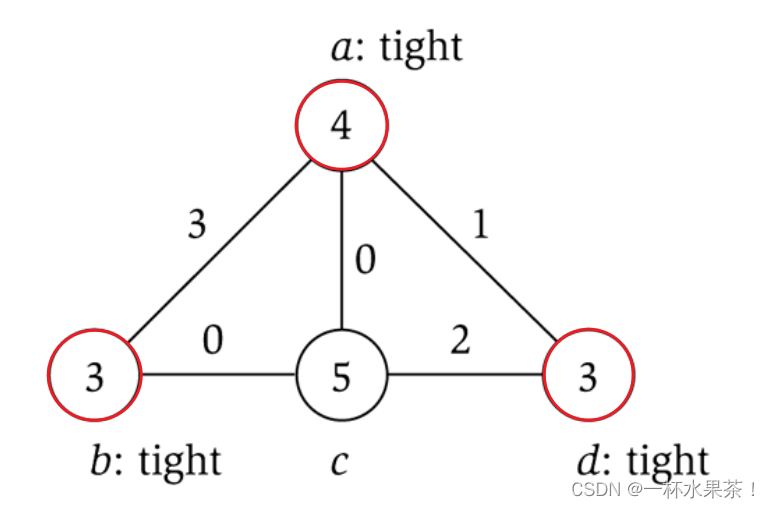
下面举个例子说明:
S = { a , b , d } S=\{a,b,d\} S={a,b,d} 是一个顶点覆盖,边的价格 p e p_e pe 标注在边的旁边,顶点的权值 w i w_i wi 在顶点中给出,
- ∑ e ∈ E p e = 3 + 0 + 1 + 0 + 2 = 6 \displaystyle \sum_{e \in E} p_e = 3 + 0 + 1 + 0 + 2 = 6 e∈E∑pe=3+0+1+0+2=6 (所有边权之和 p ( a , b ) + p ( a , c ) + p ( a , d ) + p ( b , c ) + p ( c , d ) p_{(a,b)}+p_{(a,c)}+p_{(a,d)}+p_{(b,c)}+p_{(c,d)} p(a,b)+p(a,c)+p(a,d)+p(b,c)+p(c,d))
- ∑ i ∈ S ∑ e = ( i , j ) p e = ( 3 + 0 + 1 ) + ( 3 + 0 ) + ( 1 + 2 ) = 10 \displaystyle \sum_{i \in S} \sum_{e=(i,j)}p_e = (3+0+1) + (3+0)+(1+2) = 10 i∈S∑e=(i,j)∑pe=(3+0+1)+(3+0)+(1+2)=10 (在 S S S 中的顶点 a , b , c a,b,c a,b,c 的关联的边的和,其中 p ( a , b ) p_{(a,b)} p(a,b) 和 p ( a , d ) p_{(a,d)} p(a,d) 加了两次,因为边 ( a , b ) (a,b) (a,b) 和 ( a , d ) (a,d) (a,d) 的两个端点都在 S S S 中)
- ∑ i ∈ S w i = 4 + 3 + 3 = 10 \displaystyle \sum_{i \in S}w_i = 4 + 3 + 3 = 10 i∈S∑wi=4+3+3=10 (在 S S S 中的顶点 a , b , c a,b,c a,b,c 的权值之和 w a + w b + w c w_a+w_b+w_c wa+wb+wc)
综上, ∑ e ∈ E p e ⩽ ∑ i ∈ S ∑ e = ( i , j ) p e ⩽ ∑ i ∈ S w i = w ( S ) \displaystyle \sum_{e \in E} p_e \leqslant \displaystyle \sum_{i \in S} \sum_{e=(i,j)}p_e \leqslant \displaystyle \sum_{i \in S}w_i = w(S) e∈E∑pe⩽i∈S∑e=(i,j)∑pe⩽i∈S∑wi=w(S)
定价法近似算法
近似算法的目标是:找到一个顶点覆盖 & 同时确定价格。
- 认为算法 在如何确定价格方面是贪心的,然后用这些价格选择顶点覆盖的顶点。
定价法/竞价法 简单理解为:
- 边给相邻的点支付保护费,以保证自己能被至少一个点保护(覆盖);
- 而点收到来自各条相邻边支付的保护费之和刚好是它的权值,才能保护它们。
- 这样,那些收到保护费刚好是自身权值的点构成一个顶点覆盖。
算法过程:
- 选出还未被保护的边,提最少的价使得其相邻点至少有一个能保护它,这些能保护(覆盖)临近边的点称其为紧(tight)的,将其加入点覆盖集合。
- 循环操作,直至所有边都能被保护。
如果 ∑ e = ( i , j ) p e = w i \displaystyle \sum_{e=(i,j)}p_e = w_i e=(i,j)∑pe=wi,则称顶点 i i i 是紧的(或“付清的”)。

定价法近似算法例子
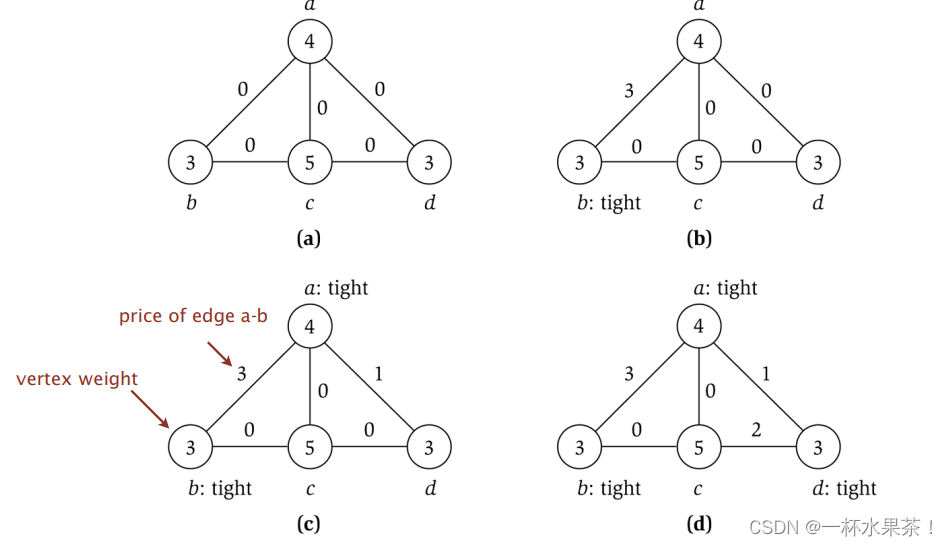
- 开始时没有一个顶点是紧的,算法决定选择边 ( a , b ) (a,b) (a,b),可以把 ( a , b ) (a,b) (a,b) 支付的价格提高到 3,这时顶点 b b b 变成紧的,不能再提高了。
- 然后算法选择边 ( a , d ) (a,d) (a,d),只能把它的价格提高到 1,因为这时顶点 a a a 变成紧的( a a a 的权等于 4,它还与一条支付 3 的边关联)。
- 最后,算法选择边 ( c , d ) (c,d) (c,d),可以把它支付的价格提高到 2,这时顶点 d d d 变成紧的。
- 现在所有的边都至少有一个端点是紧的,因此算法终止。
- 紧的顶点是 { a , b , d } \{a,b,d\} {a,b,d} ,这是得到的顶点覆盖(注意这不是最小顶点覆盖,选择 a a a 和 c c c 可以得到最小权顶点覆盖)。
注意:如果边 e e e 的两个端点都在这个顶点覆盖中,那么 e e e 可能不得不为两个顶点支付。如,边 ( a , b ) (a,b) (a,b) 和边 ( a , d ) (a,d) (a,d)。
- 但是,每一条边最多被要求支付两次它的价格(每个端点一次)。
Theorem. 近似算法返回的集合 S S S 和价格 p p p 满足不等式 w ( S ) ⩽ 2 ∑ e ∈ E p e w(S) \leqslant 2 \displaystyle \sum_{e \in E} p_e w(S)⩽2e∈E∑pe。
证明:
因为 S S S 中的所有顶点都是紧的,故对所有的 i ∈ S i \in S i∈S, ∑ e = ( i , j ) p e = w i \displaystyle \sum_{e=(i,j)}p_e = w_i e=(i,j)∑pe=wi。
对 S S S 中的所有顶点求和得到:
w ( S ) = ∑ i ∈ S w i = ∑ i ∈ S ∑ e = ( i , j ) p e w(S) = \displaystyle \sum_{i \in S}w_i = \sum_{i \in S} \sum_{e=(i,j)} p_e w(S)=i∈S∑wi=i∈S∑e=(i,j)∑pe
∑ i ∈ S ∑ e = ( i , j ) p e \displaystyle \sum_{i \in S} \sum_{e=(i,j)} p_e i∈S∑e=(i,j)∑pe 中一条边 e = ( i , j ) e=(i,j) e=(i,j) 最多可以被包含两次(如果 i i i 和 j j j 都在 S S S 中),所以
w ( S ) = ∑ i ∈ S ∑ e = ( i , j ) p e ⩽ 2 ∑ e ∈ E p e w(S)=\sum_{i \in S} \sum_{e=(i,j)} p_e \leqslant 2\sum_{e\in E}p_e w(S)=i∈S∑e=(i,j)∑pe⩽2e∈E∑pe
定价法近似算法分析
Theorem. 定价法近似算法是 WEIGHTED-VERTEX-COVER 的 2-近似 算法。即近似算法返回的集合 S S S 是一个顶点覆盖,它的费用不超过顶点覆盖最小费用的 2 倍。
证明:
由于 while 循环的每次迭代后至少有一个新节点变紧,因此算法终止。
近似算法返回的 S S S 的确是一个顶点覆盖。否则,假设 S S S 不覆盖边 e = ( i , j ) e=(i,j) e=(i,j),则顶点 i i i 和 j j j 都不是紧的,这与算法中 while 循环终止矛盾。
设 S ∗ S^* S∗ 是一个最优顶点覆盖,
由 w ( S ) ⩽ 2 ∑ e ∈ E p e w(S) \leqslant 2 \displaystyle \sum_{e \in E} p_e w(S)⩽2e∈E∑pe ,再由公平性引理有 ∑ e ∈ E p e ⩽ w ( S ∗ ) \displaystyle \sum_{e \in E} p_e \leqslant w(S^*) e∈E∑pe⩽w(S∗),则
w ( S ) ⩽ 2 ∑ e ∈ E p e ⩽ 2 w ( S ∗ ) w(S) \leqslant 2 \displaystyle \sum_{e \in E} p_e \leqslant 2w(S^*) w(S)⩽2e∈E∑pe⩽2w(S∗)
可证。
LP rounding: weighted vertex cover
weighted vertex cover
给定一个带有顶点权重 w i ≥ 0 w_i ≥ 0 wi≥0 的图 G = ( V , E ) G = (V, E) G=(V,E),找到一个权重最小的顶点子集 S ⊆ V S ⊆ V S⊆V,使得每条边都至少有一个顶点在 S S S 中。
Weighted vertex cover: ILP formulation
Integer linear programming formulation. 整数线性规划建模
- 使用 0/1 变量 x i x_i xi 来建模每个顶点 i i i 的包含:
x i = { 0 , 顶点 i 不在顶点覆盖中 1 , 顶点 i 在顶点覆盖中 x_i = \begin{cases} 0, 顶点 i 不在顶点覆盖中\\ 1, 顶点 i 在顶点覆盖中 \end{cases} xi={0,顶点i不在顶点覆盖中1,顶点i在顶点覆盖中
顶点覆盖与 0/1 赋值一一对应: S = { i ∈ V : x i = 1 } S = \{ i ∈ V : x_i = 1 \} S={i∈V:xi=1}
-
目标函数:最小化 ∑ i w i x i \displaystyle \sum_i w_i x_i i∑wixi。
-
约束条件:对于每条边 ( i , j ) (i, j) (i,j),必须取顶点 i i i 或 j j j (或两者都取): x i + x j ≥ 1 x_i + x_j ≥ 1 xi+xj≥1。

Observation. 如果 x ∗ x^* x∗ 是 I L P ILP ILP 的最优解,那么 S = { i ∈ V : x i ∗ = 1 } S = \{ i ∈ V : x_i^* = 1 \} S={i∈V:xi∗=1} 是一个最小权重的顶点覆盖。
给定整数 a i j , b i a_{ij}, b_i aij,bi 和 c j c_j cj,找到满足以下条件的 整数 x j x_j xj:
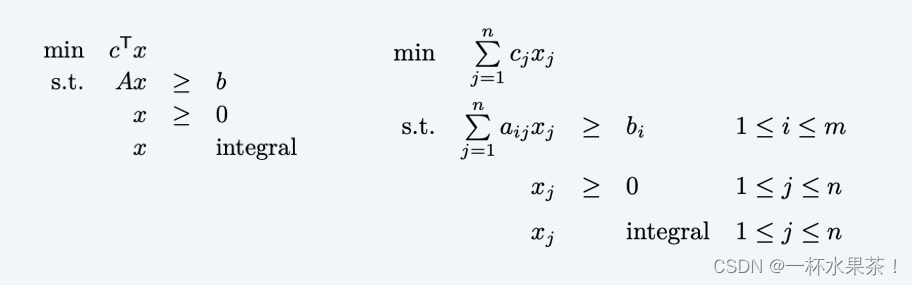
Observation. 顶点覆盖的公式证明了整数规划是一个 NP-难 的优化问题。
给定整数 a i j , b i a_{ij}, b_i aij,bi 和 c j c_j cj,找到满足以下条件的 实数 x j x_j xj:

LP 可行域
下图是一个简单的线性规划可行域:
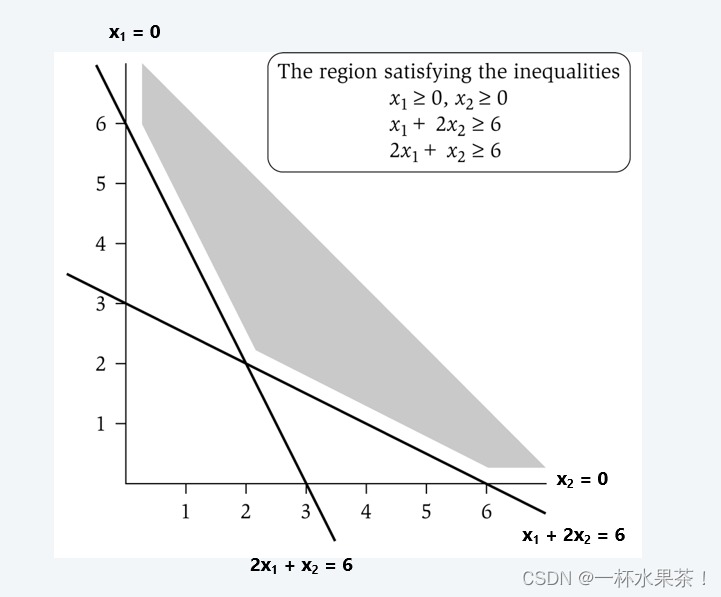
观察:LP 的最优值 ≤ ILP的最优值。
证明:LP 具有较少的约束(可以不是整数)。
注意:LP 解 x ∗ x^* x∗可能不对应于顶点覆盖。(即使所有权重都是 1)
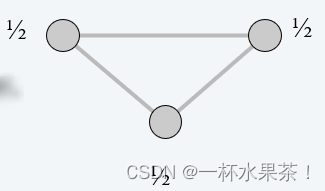
Q:求解 LP 如何帮助我们找到一个低权重的顶点覆盖?
A:求解 LP 并舍入 x ∗ x^* x∗ 中的分数值。
引理:如果 x ∗ x^* x∗ 是最优的 LP 解,那么 S = { i ∈ V : x i ∗ ⩾ 1 / 2 } S=\{ i \in V: x_i^* \geqslant 1/2\} S={i∈V:xi∗⩾1/2} 是一个顶点覆盖,并且权值最多是最小权值的两倍。
证明:
先证 S S S 是一个顶点覆盖:考虑任意一条边 ( i , j ) ∈ E (i,j)\in E (i,j)∈E,由于 x i ∗ + x j ∗ ⩾ 1 x_i^* + x_j^* \geqslant 1 xi∗+xj∗⩾1,则 x i ∗ ⩾ 1 / 2 x_i^* \geqslant 1/2 xi∗⩾1/2 或者 x j ∗ ⩾ 1 / 2 x_j^* \geqslant 1/2 xj∗⩾1/2 或者两者都,那么 ( i , j ) (i,j) (i,j) 被覆盖。
再证 S S S 有期望的权值:设 S ∗ S^* S∗ 是最优的顶点覆盖,那么
∑ i ∈ S ∗ w i ⩾ ∑ i ∈ S w i x i ∗ ⩾ 1 2 ∑ i ∈ S w i \displaystyle \sum_{i \in S^*}w_i \geqslant \sum_{i \in S}w_i x_i^* \geqslant \frac{1}{2} \sum_{i \in S}w_i i∈S∗∑wi⩾i∈S∑wixi∗⩾21i∈S∑wi
- 第一个不等号是因为 LP 的最优值 ≤ ILP的最优值,这是因为 LP 具有更少的约束。
- 第二个不等号是因为 x i ∗ ⩾ 1 / 2 x_i^* \geqslant 1/2 xi∗⩾1/2。
定理:舍入算法 是一种 2-近似 算法。
证明:引理 + LP 可以在多项式时间内求解的事实。
Poly-time reductions
Reduction
假设我们能在多项式时间内解决问题 Y Y Y,那么在多项式时间还能解决什么呢?
Reduction. 如果问题 X X X 的任意实例可以使用以下公式求解,则 问题 X X X 的多项式时间可 归约 为问题 Y Y Y:
- 标准计算步骤的多项式数,
- 解决问题 Y Y Y 的对 oracle 的多项式调用数。(oracle 是由特殊硬件补充的计算模型,可在一步中解决 Y Y Y 的实例)
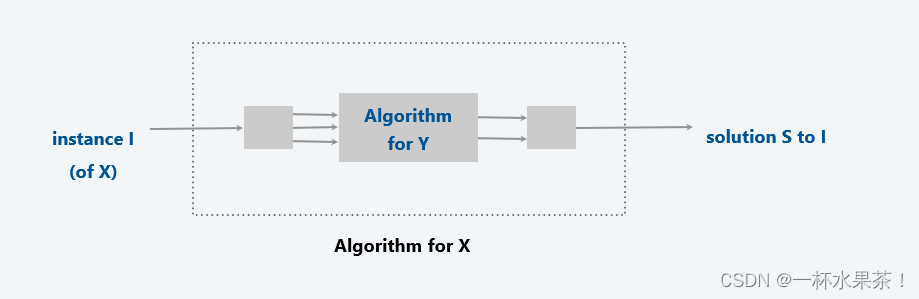
符号: X ≤ P Y X≤_P Y X≤PY。
注意:我们花时间写下发送到 oracle 的 Y Y Y 的实例必须是多项式大小。
新手易错:混淆 X ≤ P Y X≤_P Y X≤PY 与 Y ≤ P X Y≤_P X Y≤PX。
Design algorithms. 如果 X ≤ P Y X≤_P Y X≤PY ,且 Y Y Y 可以在多项式时间内求解,那么 X X X 可以在多项式时间内求解。
建立不可解性:如果 X ≤ P Y X≤_P Y X≤PY ,且 X X X 不能在多项式时间内求解,则 Y Y Y 不能在多项式时间内求解。
建立等价性:如果 X ≤ P Y X ≤_P Y X≤PY 且 Y ≤ P X Y ≤_P X Y≤PX,我们使用符号 X ≡ P Y X ≡_P Y X≡PY。在这种情况下, X X X 可以在多项式时间内解决当且仅当 Y Y Y 也可以。
结论:归约可以根据问题的相对难度进行分类。
Independent set
Independent-Set. 给定一个图 G = ( V , E ) G=(V, E) G=(V,E) 和一个整数 k k k,是否存在 k k k(或更多)顶点的子集,使得子集中的 任意两个顶点都不相邻?

Vertex cover
Vertex-Cover. 给定一个图 G = ( V , E ) G=(V, E) G=(V,E) 和一个整数 k k k,是否存在 k k k(或更少)顶点的子集,使得每条边都入射到子集中 至少有一个顶点?
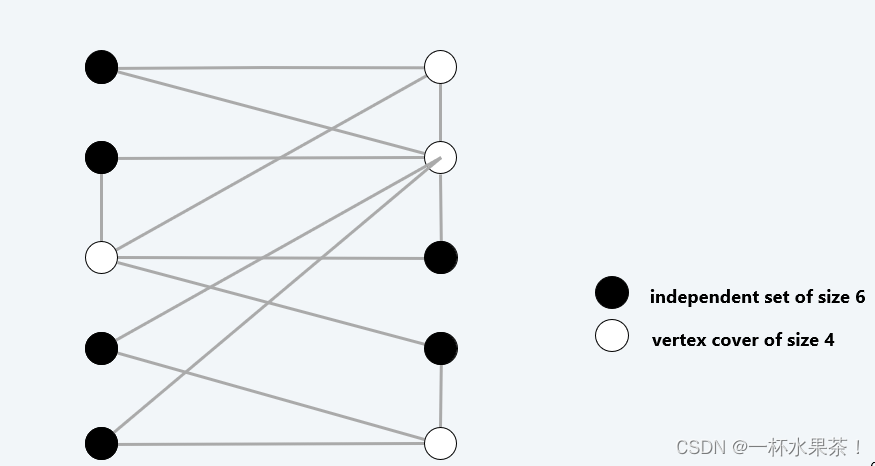
Vertex cover and independent set reduce to one another
定理: I n d e p e n d e n t − S e t ≡ P V e r t e x − C o v e r Independent-Set \ ≡_P \ Vertex-Cover Independent−Set ≡P Vertex−Cover.
证明:我们证明 S S S 是大小为 k k k 的独立集,当且仅当 V − S V−S V−S 是大小为 n – k n–k n–k 的顶点覆盖。
- 充分性证明
设 S S S 是一个大小为 k k k 的独立集, V − S V − S V−S 的大小为 n – k n – k n–k。
考虑任意一条边 ( u , v ) ∈ E (u, v) ∈ E (u,v)∈E,
S S S 独立 ⇒ u ∉ S u ∉ S u∈/S 或 v ∉ S v ∉ S v∈/S 或两者都不在 S S S 中 ⇒ u ∈ V − S u ∈ V − S u∈V−S 或 v ∈ V − S v ∈ V − S v∈V−S 或两者都在 V − S V − S V−S 中。 因此, V − S V − S V−S 覆盖了 ( u , v ) (u, v) (u,v)。
- 必要性证明
设 V − S V − S V−S 是一个大小为 n – k n – k n–k 的顶点覆盖, S S S 的大小为 k k k。
考虑任意一条边 ( u , v ) ∈ E (u, v) ∈ E (u,v)∈E,
V − S V − S V−S 是一个顶点覆盖 ⇒ u ∈ V − S u ∈ V − S u∈V−S 或 v ∈ V − S v ∈ V − S v∈V−S 或两者都在 V − S V − S V−S 中 ⇒ u ∉ S u ∉ S u∈/S 或 v ∉ S v ∉ S v∈/S 或两者都不在 S S S 中。
因此, S S S 是一个独立集。
Set-Cover 集合覆盖
Set-Cover. 给定一个元素集合 U U U,一个 U U U 的子集合的集合 S S S,和一个整数 k k k,是否存在 ≤ k ≤ k ≤k 个这样的子集合,它们的 并集等于 U U U?
举个例子, m m m 个可用的软件,我们希望我们的系统具有的 n n n 个功能的集合 U U U。第 i i i 个软件提供了 U U U 的子集 S i S_i Si 的功能。目标:使用最少的软件实现所有 n n n 个功能。

Vertex cover reduces to set cover
定理: V e r t e x − C o v e r ≤ P S e t − C o v e r Vertex-Cover \ ≤_P \ Set-Cover Vertex−Cover ≤P Set−Cover.
证明:给定一个顶点覆盖问题的实例 G = ( V , E ) G = (V, E) G=(V,E) 和 k k k,我们构造一个集合覆盖问题的实例 ( U , S , k ) (U, S, k) (U,S,k),使得 U U U 有大小为 k k k 的集合覆盖当且仅当 G G G 有大小为 k k k 的顶点覆盖。
构造方法:全集 U = E U = E U=E。 对于每个结点 v ∈ V v ∈ V v∈V,包含一个子集 S v = { e ∈ E : e 与 v 相邻 } S_v = \{e ∈ E : e 与 v 相邻 \} Sv={e∈E:e与v相邻}。
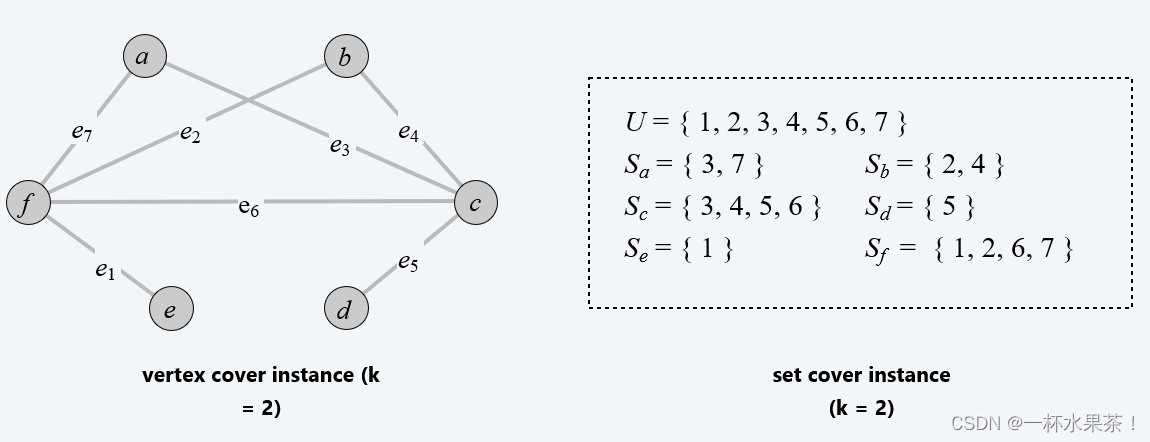
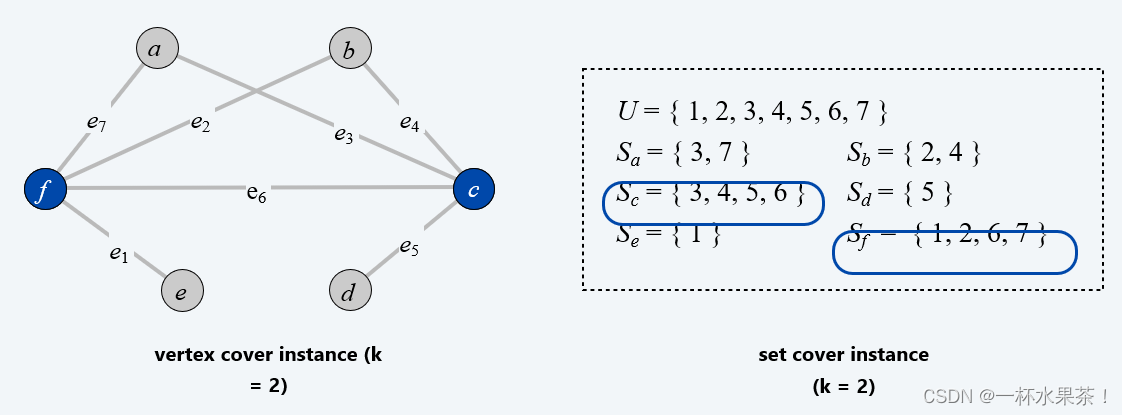
引理:如果 G = ( V , E ) G = (V, E) G=(V,E) 包含一个大小为 k k k 的顶点覆盖,那么 ( U , S , k ) (U, S, k) (U,S,k) 包含一个大小为 k k k 的集合覆盖,反之亦然。
证明:
- 充分性证明
设 X ⊆ V X ⊆ V X⊆V 是 G G G 中的一个大小为 k k k 的顶点覆盖。 那么 Y = { S v : v ∈ X } Y = \{ S_v : v ∈ X \} Y={Sv:v∈X} 是一个大小为 k k k 的集合覆盖。
- 必要性证明
设 Y ⊆ S Y ⊆ S Y⊆S 是 ( U , S , k ) (U, S, k) (U,S,k) 中的一个大小为 k k k 的集合覆盖。 那么 X = { v : S v ∈ Y } X = \{ v : S_v ∈ Y \} X={v:Sv∈Y} 是 G 中的一个大小为 k k k 的顶点覆盖。
Satisfiability

SAT. 给定一个合取范式(CNF)公式 Φ \Phi Φ ,它是否有一个满足的真值赋值?
3 − S A T 3-SAT 3−SAT 是一个特殊的 SAT 问题,其中每个子句恰好包含 3 个文字(并且每个文字对应于不同的变量)。
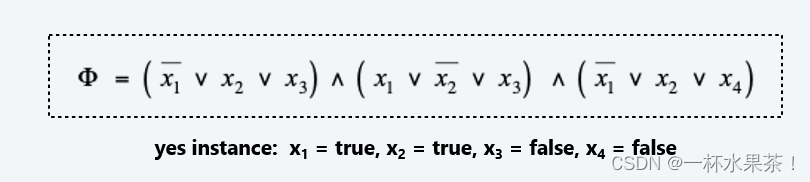
3-satisfiability reduces to independent set
定理: 3 − S a t ≤ P I n d e p e n d e n t − S e t 3-Sat \ ≤_P \ Independent-Set 3−Sat ≤P Independent−Set.
证明:
给定一个 3 − S A T 3-SAT 3−SAT 问题的实例 Φ \Phi Φ,我们构造一个独立集问题的实例 ( G , k ) (G, k) (G,k) ,使得 G G G 有一个大小为 $k = \left| \Phi \right| $ 的独立集当且仅当 Φ \Phi Φ 是可满足的。
构造方法:
・ G G G 包含每个子句的 3 个结点,每个结点对应一个文字。
・将一个子句中的 3 个文字用三角形连接起来。
・将每个文字和它的否定连接起来。
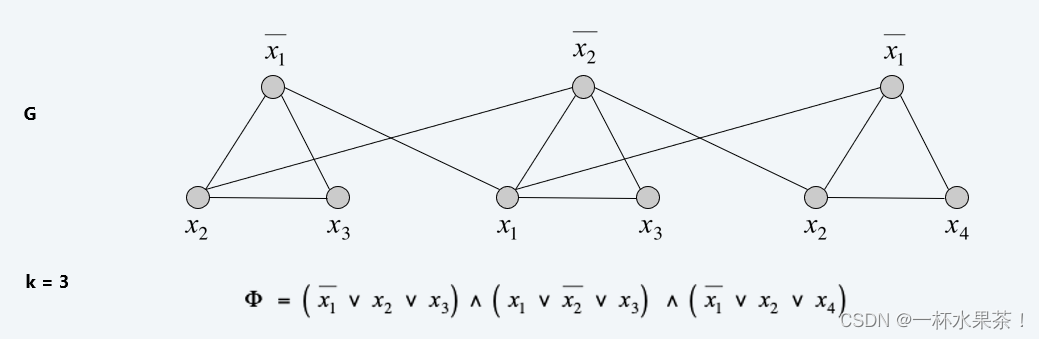
引理:如果 Φ \Phi Φ 是可满足的,那么 G G G 包含一个大小为 k = ∣ Φ ∣ k = \left| \Phi \right| k=∣Φ∣ 的独立集,反之亦然。
证明:
- 充分性证明
考虑 Φ \Phi Φ 的任意一个满足的真值赋值。 从每个子句/三角形中选择一个真值为真的文字。 这是一个大小为 k = ∣ Φ ∣ k = \left| \Phi \right| k=∣Φ∣ 的独立集。
- 必要性证明
设 S S S 是一个大小为 k k k 的独立集。 S S S 必须在每个三角形中包含恰好一个结点。 将这些文字设为真(并且保持剩余文字的一致性)。 Φ Φ Φ 中的所有子句都被满足。
Review
基本的归约策略:
简单等价:独立集问题与顶点覆盖问题多项式等价, I n d e p e n d e n t − S e t ≡ P V e r t e x − C o v e r Independent-Set \ ≡_P \ Vertex-Cover Independent−Set ≡P Vertex−Cover
特殊情况到一般情况:顶点覆盖问题多项式归约到集合覆盖问题, V e r t e x − C o v e r ≤ P S e t − C o v e r Vertex-Cover \ ≤_P \ Set-Cover Vertex−Cover ≤P Set−Cover
利用小构件进行编码:3-SAT问题多项式归约到独立集问题, 3 − S a t ≤ P I n d e p e n d e n t − S e t 3-Sat \ ≤_P \ Independent-Set 3−Sat ≤P Independent−Set
传递性:如果 X ≤ P Y X ≤_P Y X≤PY 并且 Y ≤ P Z Y ≤_P Z Y≤PZ,那么 X ≤ P Z X ≤_P Z X≤PZ。
证明思路:将两个算法组合起来。
Ex. 3 − S a t ≤ P I n d e p e n d e n t − S e t ≤ P V e r t e x − C o v e r ≤ P S e t − C o v e r 3-Sat \ ≤_P \ Independent-Set \ ≤_P \ Vertex-Cover \ ≤_P \ Set-Cover 3−Sat ≤P Independent−Set ≤P Vertex−Cover ≤P Set−Cover
Hamilton
Hamilton cycle
HAMILTON-CYCLE.(哈密顿回路) 给定一个无向图 G = ( V , E ) G = (V, E) G=(V,E),是否存在一个循环 $ \Gamma$,它恰好访问每个结点一次?
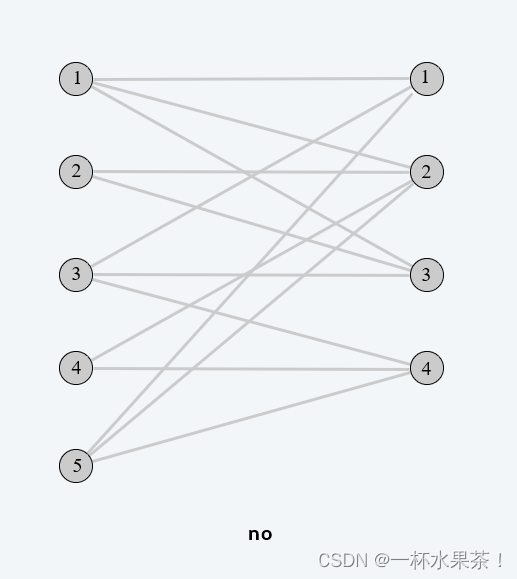
DIRECTED-HAMILTON-CYCLE. (有向哈密顿回路) 给定一个有向图 G = ( V , E ) G = (V, E) G=(V,E),是否存在一个有向循环 Γ \Gamma Γ,它恰好访问图中的每个结点一次?
定理:DIRECTED-HAMILTON-CYCLE ≤ P ≤_P ≤P HAMILTON-CYCLE
证明:给定一个有向图 G = ( V , E ) G = (V, E) G=(V,E),构造一个有 3 n 3n 3n 个结点的图 G ʹ G^ʹ Gʹ。
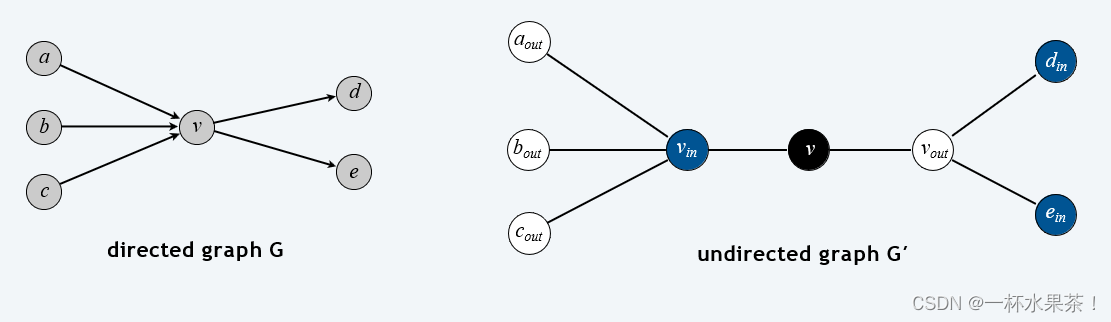
Directed Hamilton cycle reduces to Hamilton cycle
引理: G G G 有一个有向哈密尔顿回路 当且仅当 G ʹ G^ʹ Gʹ 有一个哈密尔顿回路。
哈密尔顿回路是指一个 图中的一个回路,它恰好经过图中的每个顶点一次。
有向哈密尔顿回路是指一个 有向图中的一个有向回路,它恰好经过有向图中的每个顶点一次。
3-satisfiability reduces to directed Hamilton cycle
定理:3-SAT ≤ P ≤_P ≤P DIRECTED-HAMILTON-CYCLE.








![[C#][opencvsharp]C#使用opencvsharp进行年龄和性别预测支持视频图片检测](https://img-blog.csdnimg.cn/direct/ce6fe244d81a49caa29af93f58bb06a8.png)