引言

介绍动态规划（DP）在解决子数组问题上的重要性，以及本文的目的——通过具体问题的分析和代码示例，帮助读者理解如何用DP解决子数组问题。

子数组问题介绍

简要介绍什么是子数组问题，以及这些问题在实际应用中的重要性。例如，最大子数组和问题、最长递增子数组问题等。

动态规划的基本概念

解释动态规划的基本思想：通过将问题分解为子问题，保存子问题的解来避免重复计算，从而提高算法效率。可以简单介绍状态、状态转移方程和初始条件等基本概念。

具体问题的解决方法

最大子数组和问题（Maximum Subarray Sum）
问题描述：
给定一个整数数组，找出和最大的连续子数组，并返回其最大和。

动态规划解法：

定义状态：dp[i]表示以第i个元素结尾的最大子数组和。
状态转移方程：dp[i] = max(nums[i], dp[i-1] + nums[i])
即对于第i个元素，最大子数组和要么是自己，要么是前一个元素的最大子数组和加上自己。
初始状态：dp[0] = nums[0]
结果：max(dp)，即所有dp[i]中的最大值。

关于子数组问题的几个题

1.最大子数组和

题目链接
题目：

样例输出和输入：

题目要求很简单，就是求出 最长的子数组的和，这个和有一个要求就是和最大。
算法原理：
状态表示：dp[i]表示以i位置为结尾时所有子数组的和中最大的那个。
状态转移方程：
分析：到达i位置时i位置最长的子数组的和应该等于i-1位置的最长子数组的和加上当前i位置的值，还有一种情况：单独分析，就是当前位置的数就是一个子数组，长度为1，所以，dp[i]=max(dp[i-1]+nums[i],nums[i])。
代码展示：

class Solution {
public:int maxSubArray(vector<int>& nums){int n = nums.size();vector<int> dp(n);dp[0] = nums[0];for (int i = 1;i < n;i++){dp[i] = max(dp[i - 1] + nums[i], nums[i]);}int  Max = -0x3f3f3f3f;for (int i = 0;i < n;i++){Max = max(dp[i], Max);}return Max;}
};

运行结果：

2.环形子数组的最大和

题目链接
题目：

样例输出和输入：

这道题在第一道题的基础上加了一个条件，就是这是个环形数组头和尾是相连的。也让我们求子数组中和最大的那个。
算法原理：
状态表示：分析：明显这道题一个状态是表示不了的，因为这个子数组可能连续也可能不连续，由于求的最大的值，所以第一种情况：当子数组在中间时最大，还有一种情况，子数组在两边时不连续的时候最大 ，当不连续的时候 最大，也就是中间的最小。这两种状态分别为f[i]和g[i]。

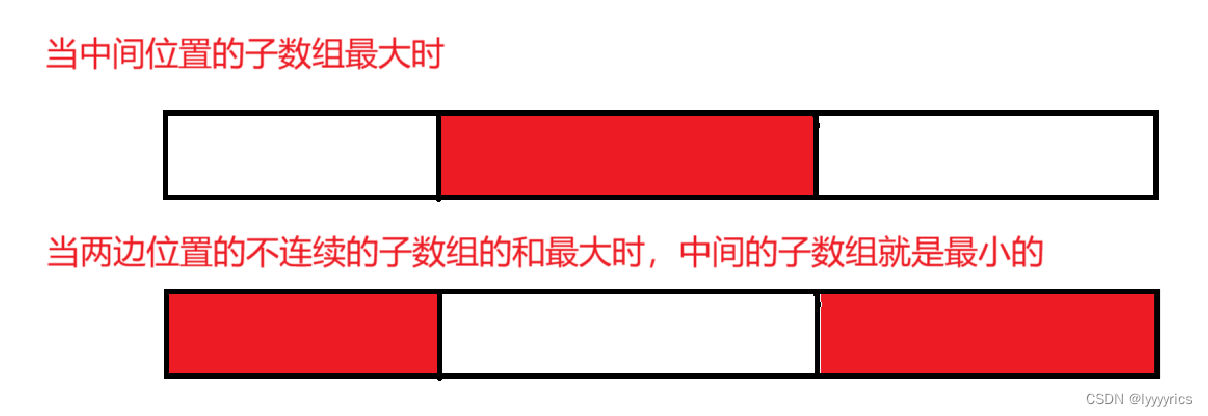
状态转移方程：先分析中间最大的时候的状态，当到达i位置的时候i位置的最大的子数组的和就是前一个位置i-1的位置的最大的子数组的和加上当前i位置的值，还有一种情况就是i位置自身成一个长度为1的数组。f[i] = max(f[i - 1] + nums[i-1], nums[i-1])，g[i]也同理，g[i]为当前位置的子数组中最小的那个 子数组的和，所以i位置的子数组和的最小等于前一个位置的子数组和的最小，加上当前位置，g[i - 1] + nums[i-1]最后还要取一个min，g[i] = min(g[i - 1] + nums[i-1], nums[i-1])

代码展示：

class Solution {
public:int maxSubarraySumCircular(vector<int>& nums){int n = nums.size();vector<int> f(n + 1), g(n + 1);int sum = 0;int fmax = INT_MIN;int gmin = INT_MAX;for (int i = 1;i <= n;i++){f[i] = max(f[i - 1] + nums[i-1], nums[i-1]);fmax = max(f[i], fmax);g[i] = min(g[i - 1] + nums[i-1], nums[i-1]);gmin = min(gmin, g[i]);sum += nums[i - 1];}return sum == gmin ? fmax : max(fmax, sum - gmin);}
};

运行结果：

3.乘积最大子数组

题目链接
题目：

样例输出和输入：

这道题的题意和前两道题也大差不差，就是让我们求最大乘积的子数组的乘积。
算法原理：
状态表示：这道题还是需要两个状态，因为有负数情况，不一定是正数乘正数才是最大的，两个负数相乘也 有可能是最大的。f[i]表示以i位置为结尾的子数组中的最大乘积的那个，g[i]表示以i位置为结尾的子数组中最小的乘积的那个。
状态转移方程：首先分析f[i]这个状态，这个状态有三个子状态，第一种状态是i位置是负数时，所以负数应乘上最小的才是最大的，还有一种状态就是当前位置是正数，所以当前位置应该乘上前一个位置中最大的那个子数组的乘积。还有一个情况就是单独成为一个子数组。

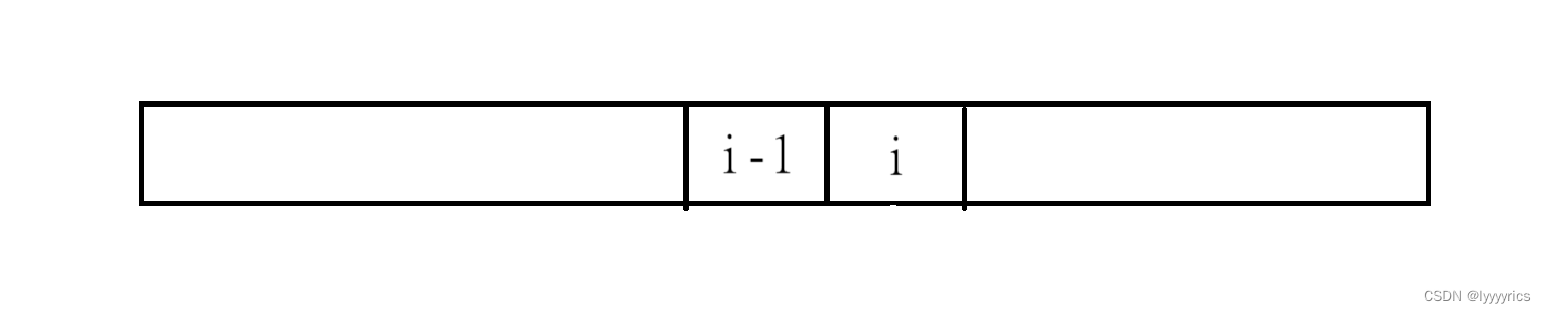
max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]))
g[i]的状态转移方程也可以用类似的方法进行分析：min(nums[i - 1], min(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]))

代码展示：

class Solution {
public:int maxProduct(vector<int>& nums){int n = nums.size();vector<double> f(n + 1), g(n + 1);//f是最大的，g是最小的g[0] = 1, f[0] = 1;double ret = INT_MIN;for (int i = 1;i <= n;i++){double x = nums[i - 1], y = f[i - 1] * nums[i - 1], z = g[i - 1] * nums[i - 1];f[i] = max(x, max(y, z));g[i] = min(x, min(y, z));ret = max(f[i], ret);}return ret;}
};

运行结果：

4.乘积为正数的最长子数组长度

题目链接
题目：

样例输出和输入：

这道题要求的是乘积是正数的子数组总长度最长的那个子数组的长度。
算法原理：
状态表示：由于两个负数相乘也是正数，所以状态表示的时候我们也要记录负数的状态，f[i]表示以i位置为结尾的所有子数组中乘积是正数的最长的子数组的长度，g[i]]是以i位置为结尾的子数组中乘积为负数的最长子数组的长度。
状态转移方程：需要判断i位置的值是正数还是负数，如果是负数的话就是就需要用前一个位置的负数子数组的最长的那个加一，也就是g[i-1]+1但是前i-1个有可能没有小于零的，所以这里f[i]是有可能是零的，所以这里需要判断一下i-1位置时的g[i-1]的值，当当前值大于零的时候f[i]就等于 前一个位置的f[i-1]+1,同理负数的最长子数组也可以分析出来，状态转移方程：这是大于零的两种状态的情况：g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1，f[i] = f[i - 1] + 1小于零的两种状态的情况：f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1，g[i] = f[i - 1] + 1。

代码展示：

class Solution {
public:int getMaxLen(vector<int>& nums) {int n = nums.size();if (n == 1){return nums[0] > 0;}vector<int> f(n), g(n);f[0] = nums[0] > 0, g[0] = nums[0] < 0;int fmax = 0;for (int i = 1;i < n;i++){if (nums[i] > 0){f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;fmax = max(f[i], fmax);}else if (nums[i] < 0){f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;fmax = max(f[i], fmax);}}return fmax;}
};

运行结果：

5.等差数列划分

题目链接
题目：

样例输出和输入：

这道题题意很简单，就是让我们求所有能构成等差数列的子数组的总和
算法原理：
等差数列性质：2a=c+ba为等差中项。
状态表示：dp[i]为以i位置为结尾的所有子数组中的等差数列的个数。
状态转移方程：先判断i位置的前两个位置是否 满足上述的等差数列的性质：如果满足则dp[i]=dp[i - 1] + 1因为满足，所以dp[i-1]位置需要算上，但是又多了一个子数组，这个子数组 就是满足的那个三个数的子数组。不满足的话,dp[i]直接就是0.
代码展示：

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if (n < 3){return  0;}vector<int>  dp(n);dp[0] = 0, dp[1] = 0;int count = 0;for (int i = 2;i < n;i++){dp[i] = nums[i] + nums[i - 2] == 2 * nums[i - 1] ? dp[i - 1] + 1 : 0;}for(int i=0;i<n;i++){count+=dp[i];}return count;}
};

运行结果：

总结

通过本文的介绍，我们详细探讨了动态规划在解决子数组问题中的应用，具体分析了最大子数组和问题和最长递增子数组问题。这些问题在实际生活中的数据处理、优化等场景中有着广泛的应用。动态规划通过将问题分解为子问题，保存子问题的解，避免了重复计算，从而大大提高了算法的效率。

在学习和应用动态规划的过程中，我们需要明确状态、状态转移方程和初始条件。通过练习具体问题，我们可以更深入地理解动态规划的思想和方法。无论是最大子数组和问题还是最长递增子数组问题，掌握了动态规划的基本原理后，我们可以更灵活地应对其他类似的问题。

希望这篇文章能帮助你更好地理解动态规划在子数组问题中的应用。如果你有任何问题或建议，欢迎在评论区留言，我们将尽力为你解答。祝你在学习动态规划和解决实际问题的过程中取得更多的进步！