1. 为什么学习KNN算法

KNN是监督学习分类算法，主要解决现实生活中分类问题。根据目标的不同将监督学习任务分为了分类学习及回归预测问题。

KNN（K-Nearest Neihbor，KNN）K近邻是机器学习算法中理论最简单，最好理解的算法，是一个非常适合入门的算法，拥有如下特性：

• 思想极度简单，应用数学知识少(近乎为零)，对于很多不擅长数学的小伙伴十分友好
• 虽然算法简单，但效果也不错

2. KNN 原理

上图中每一个数据点代表一个肿瘤病历：

• 横轴表示肿瘤大小，纵轴表示发现时间
• 恶性肿瘤用蓝色表示，良性肿瘤用红色表示

疑问：新来了一个病人(下图绿色的点)，如何判断新来的病人(即绿色点)是良性肿瘤还是恶性肿瘤？

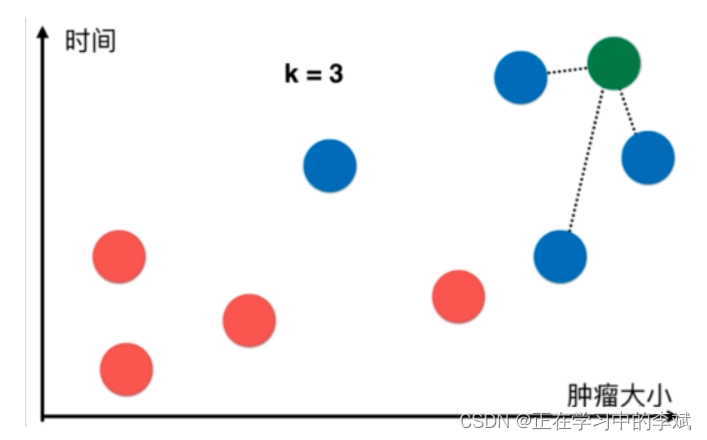
解决方法：k-近邻算法的做法如下：
（1）取一个值k=3(k值后面介绍，现在可以理解为算法的使用者根据经验取的最优值)
（2）在所有的点中找到距离绿色点最近的三个点
（3）让最近的点所属的类别进行投票
（4）最近的三个点都是蓝色的，所以该病人对应的应该也是蓝色，即恶性肿瘤。

3. 距离度量方法

机器学习算法中，经常需要 判断两个样本之间是否相似 ，比如KNN，K-means，推荐算法中的协同过滤等等，常用的套路是 将相似的判断转换成距离的计算 ，距离近的样本相似程度高，距离远的相似程度低。所以度量距离是很多算法中的关键步骤。

KNN算法中要求数据的所有特征都用数值表示。若在数据特征中存在非数值类型，必须采用手段将其进行量化为数值。

• 比如样本特征中包含有颜色（红、绿、蓝）一项，颜色之间没有距离可言，可通过将颜色转化为 灰度值来实现距离计算 。
• 每个特征都用数值表示，样本之间就可以计算出彼此的距离来

3.1 欧式距离

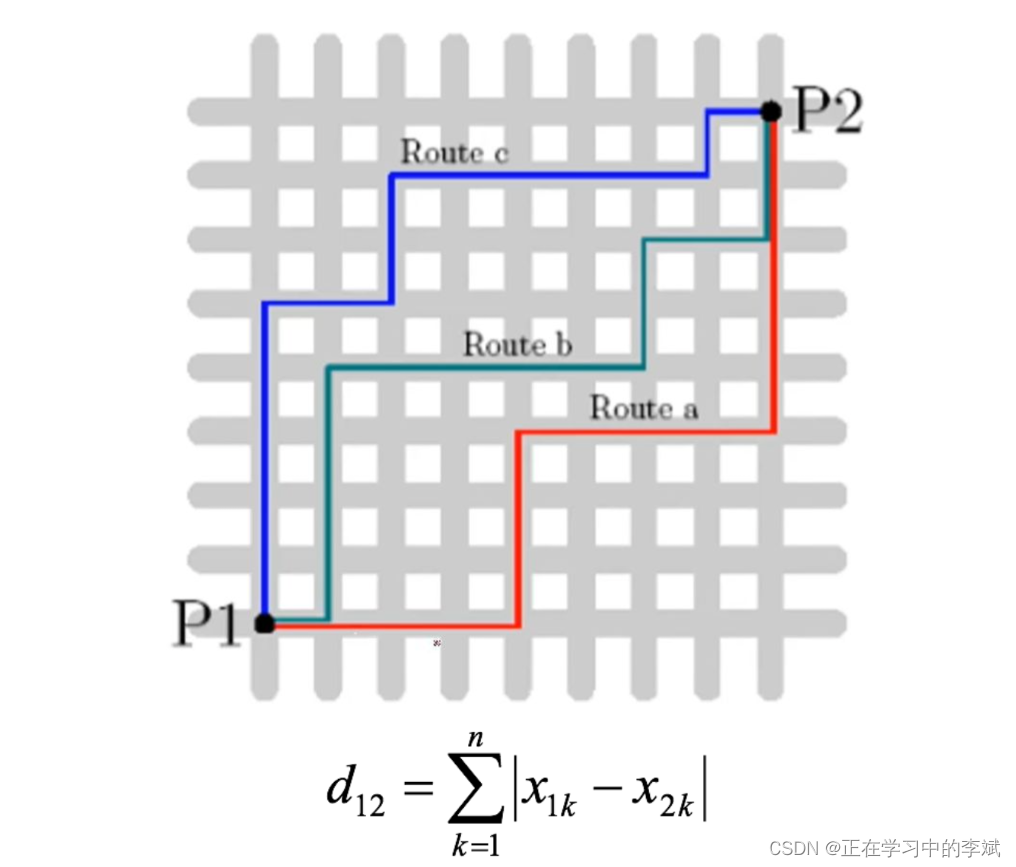
3.2 曼哈顿距离

3.3 切比雪夫距离(了解)

3.4 闵式距离

闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

其中p是一个变参数：

• 当 p=1 时，就是曼哈顿距离；
• 当 p=2 时，就是欧氏距离；
• 当 p→∞ 时，就是切比雪夫距离。

根据 p 的不同，闵氏距离可以表示某一类/种的距离。

4. 归一化和标准化

样本中有多个特征，每一个特征都有自己的定义域和取值范围，他们对距离计算也是不同的，如取值较大的影响力会盖过取值较小的参数。因此，为了公平，样本参数必须做一些归一化处理，将不同的特征都缩放到相同的区间或者分布内。

4.1 归一化

from sklearn.preprocessing import MinMaxScaler# 1. 准备数据
data = [[90, 2, 10, 40],[60, 4, 15, 45],[75, 3, 13, 46]]
# 2. 初始化归一化对象
transformer = MinMaxScaler()
# 3. 对原始特征进行变换
data = transformer.fit_transform(data)
# 4. 打印归一化后的结果
print(data)

归一化受到最大值与最小值的影响，这种方法容易受到异常数据的影响, 鲁棒性较差，适合传统精确小数据场景

4.2 标准化

from sklearn.preprocessing import StandardScaler# 1. 准备数据
data = [[90, 2, 10, 40],[60, 4, 15, 45],[75, 3, 13, 46]]
# 2. 初始化标准化对象
transformer = StandardScaler()
# 3. 对原始特征进行变换
data = transformer.fit_transform(data)
# 4. 打印归一化后的结果
print(data)

对于标准化来说，如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大

5. K 值选择问题

KNN算法的关键是什么？

答案一定是K值的选择，下图中K=3，属于红色三角形，K=5属于蓝色的正方形。这个时候就是K选择困难的时候。

使用 scikit-learn 提供的 GridSearchCV 工具, 配合交叉验证法可以搜索参数组合.

from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV# 1. 加载数据集
x, y = load_iris(return_X_y=True)# 2. 分割数据集
x_train, x_test, y_train, y_test = \train_test_split(x, y, test_size=0.2, stratify=y, random_state=0)# 3. 创建网格搜索对象
estimator = KNeighborsClassifier()
param_grid = {'n_neighbors': [1, 3, 5, 7]}
estimator = GridSearchCV(estimator, param_grid=param_grid, cv=5, verbose=0)
estimator.fit(x_train, y_train)# 4. 打印最优参数
print('最优参数组合:', estimator.best_params_, '最好得分:', estimator.best_score_)# 4. 测试集评估模型
print('测试集准确率:', estimator.score(x_test, y_test))

6. 数据集划分

为了能够评估模型的泛化能力，可以通过实验测试对学习器的泛化能力进行评估，进而做出选择。因此需要使用一个 “测试集” 来测试学习器对新样本的判别能力，以测试集上的 “测试误差” 作为泛化误差的近似。

6.1 留出法(简单交叉验证)

留出法 (hold-out) 将数据集 D 划分为两个互斥的集合，其中一个集合作为训练集 S，另一个作为测试集 T。

from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import ShuffleSplit
from collections import Counter
from sklearn.datasets import load_irisdef test01():# 1. 加载数据集x, y = load_iris(return_X_y=True)print('原始类别比例:', Counter(y))# 2. 留出法(随机分割)x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)print('随机类别分割:', Counter(y_train), Counter(y_test))# 3. 留出法(分层分割)x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, stratify=y)print('分层类别分割:', Counter(y_train), Counter(y_test))def test02():# 1. 加载数据集x, y = load_iris(return_X_y=True)print('原始类别比例:', Counter(y))print('*' * 40)# 2. 多次划分(随机分割)spliter = ShuffleSplit(n_splits=5, test_size=0.2, random_state=0)for train, test in spliter.split(x, y):print('随机多次分割:', Counter(y[test]))print('*' * 40)# 3. 多次划分(分层分割)spliter = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=0)for train, test in spliter.split(x, y):print('分层多次分割:', Counter(y[test]))if __name__ == '__main__':test01()test02()

6.2 交叉验证法

K-Fold交叉验证，将数据随机且均匀地分成k分,每次使用k-1份数据作为训练，而使用剩下的一份数据进行测试

from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold
from collections import Counter
from sklearn.datasets import load_irisdef test():# 1. 加载数据集x, y = load_iris(return_X_y=True)print('原始类别比例:', Counter(y))print('*' * 40)# 2. 随机交叉验证spliter = KFold(n_splits=5, shuffle=True, random_state=0)for train, test in spliter.split(x, y):print('随机交叉验证:', Counter(y[test]))print('*' * 40)# 3. 分层交叉验证spliter = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)for train, test in spliter.split(x, y):print('分层交叉验证:', Counter(y[test]))if __name__ == '__main__':test()

6.3 留一法

留一法( Leave-One-Out，简称LOO），即每次抽取一个样本做为测试集。

from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import LeavePOut
from sklearn.datasets import load_iris
from collections import Counterdef test01():# 1. 加载数据集x, y = load_iris(return_X_y=True)print('原始类别比例:', Counter(y))print('*' * 40)# 2. 留一法spliter = LeaveOneOut()for train, test in spliter.split(x, y):print('训练集:', len(train), '测试集:', len(test), test)print('*' * 40)# 3. 留P法spliter = LeavePOut(p=3)for train, test in spliter.split(x, y):print('训练集:', len(train), '测试集:', len(test), test)if __name__ == '__main__':test01()

6.4 自助法

每次随机从D中抽出一个样本，将其拷贝放入D，然后再将该样本放回初始数据集D中，使得该样本在下次采样时仍有可能被抽到；
这个过程重复执行m次后，我们就得到了包含m个样本的数据集D′，这就是自助采样的结果。

import pandas as pdif __name__ == '__main__':# 1. 构造数据集data = [[90, 2, 10, 40],[60, 4, 15, 45],[75, 3, 13, 46],[78, 2, 64, 22]]data = pd.DataFrame(data)print('数据集:\n',data)print('*' * 30)# 2. 产生训练集train = data.sample(frac=1, replace=True)print('训练集:\n', train)print('*' * 30)# 3. 产生测试集test = data.loc[data.index.difference(train.index)]print('测试集:\n', test)

7. 可执行示例代码

以下是 K-NN 算法的实现示例代码，使用 scikit-learn 库：

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score# 示例数据
X = np.array([[1, 2], [2, 3], [3, 4], [6, 7], [7, 8], [8, 9]])
y = np.array([0, 0, 0, 1, 1, 1])# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)# 创建KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)# 训练模型（实际上只是存储数据）
knn.fit(X_train, y_train)# 进行预测
y_pred = knn.predict(X_test)# 计算准确率，分类算法的评估
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

通过这个示例，可以看到 K-NN 算法的基本流程和实现。该算法通过计算距离来进行分类，并可以通过调整 K 值来优化模型性能。

8. K-NN 算法总结

K-NN（K-Nearest Neighbors）算法是一种基于实例的学习方法，用于分类和回归。它通过计算样本与训练集中所有样本之间的距离，选择最近的 K 个邻居，然后根据这些邻居的标签进行预测。

特点

1. 基于实例：没有显式的训练过程，直接使用训练数据进行预测。
2. 懒惰学习：训练阶段只是存储数据，实际的计算发生在预测阶段。
3. 非参数化：不对数据进行任何假设。

优点

1. 简单易实现：实现起来相对简单，理解容易。
2. 无需假设数据分布：对数据的分布没有任何假设。
3. 适用于分类和回归：可以同时用于分类和回归问题。
4. 灵活性：可以处理多类别分类问题。

缺点

1. 计算复杂度高：预测时需要计算新样本与所有训练样本的距离，计算量大，尤其是数据量大时。
2. 存储复杂度高：需要存储所有的训练数据。
3. 对噪音敏感：容易受到噪音和异常值的影响。
4. 维度灾难：高维数据时，计算距离的效果会变差，需要进行降维处理。

关键

1. 选择合适的 K 值：K 值过小容易过拟合，K 值过大容易欠拟合。通常通过交叉验证选择合适的 K 值。
2. 距离度量：常用的距离度量方法有欧氏距离、曼哈顿距离、闵可夫斯基距离等。
3. 特征缩放：在计算距离前，需要对特征进行标准化或归一化处理，以避免特征值范围差异导致的计算偏差。

过程

1. 数据准备：准备训练数据集和测试数据集。
2. 计算距离：对于每个测试样本，计算它与所有训练样本之间的距离。
3. 选择邻居：选择距离最近的 K 个邻居。
4. 投票或平均：
   • 分类：对 K 个邻居的类别进行投票，选择出现次数最多的类别作为预测结果。
   • 回归：对 K 个邻居的目标值进行平均，作为预测结果。
5. 输出结果：输出测试样本的预测结果。