基于机器学习方法的股票预测系列文章目录
一、基于强化学习DQN的股票预测【股票交易】
二、基于CNN的股票预测方法【卷积神经网络】
三、基于隐马尔可夫模型的股票预测【HMM】
文章目录
- 基于机器学习方法的股票预测系列文章目录
- 一、HMM模型简介
- (1)前向后向算法
- (2)概率计算
- (3)对数似然函数
- (4)Baum-Welch算法
- (5)预测下一个观测值
- (6)Kmeans参数初始化
- 二、Python代码分析
- (1)高斯分布函数
- (2)GaussianHMM 类
- 1 初始化
- 2 K-means参数初始化
- 3 前向算法
- 4 后向算法
- 5 观测概率计算
- 6 Baum-Welch算法
- 7 预测
- 8 预测更多时刻
- 9 解码
- (3)总结
- 三、实验分析
- (1)对股票指数建模的模型参数
- (2)不同states下的对数似然变化
- (3)不同states下的股票指数拟合效果
- (4)不同states下的误差及MSE
- (5)HMM模型单支股票预测小结
- (6)多支股票训练模型
本文探讨了利用隐马尔可夫模型(Hidden Markov Model, HMM)进行股票预测的建模方法,并详细介绍了模型的原理、参数初始化以及实验分析。HMM模型通过一个隐藏的马尔可夫链生成不可观测的状态序列,并由这些状态生成观测序列。本文假设观测概率分布为高斯分布,并利用前向后向算法进行概率计算和参数估计,完整代码放在GitHub上——Stock-Prediction-Using-Machine-Learing。
一、HMM模型简介
隐马尔可夫模型 (Hidden Markov Model, HMM模型), 是关于时序的概率模型, 描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列, 再由各个状态生成一个观测而产生观测随机序列的过程。HMM模型有两个基本假设:
- 齐次马尔可夫性假设: 即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态, 与其他时刻的状态及观测无关, 也与时刻 t无关。
- 观测独立性假设: 即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
隐马尔可夫模型由初始概率分布 π \pi π 、状态转移概率分布 A A A 以及观测概率分布 B B B 确定, 故可将隐马尔可夫模型 λ \lambda λ 用三元符号表示:
λ = ( A , B , π ) \lambda=(A, B, \pi) λ=(A,B,π)
在本次股票预测中, 可假设观测概率分布为:
P ( x ∣ i ) = 1 ( 2 π ) d ∣ Σ i ∣ exp ( − 1 2 ( x − μ i ) T Σ i − 1 ( x − μ i ) ) P(x \mid i)=\frac{1}{\sqrt{(2 \pi)^{d}\left|\Sigma_{i}\right|}} \exp \left(-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)^{T} \Sigma_{i}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)\right) P(x∣i)=(2π)d∣Σi∣1exp(−21(x−μi)TΣi−1(x−μi))
由此得到高斯隐马尔可夫模型。
股票价格是可以看作连续值,所以利用隐马尔可夫模型对股票进行建模时,假设观测概率为高斯分布,然后便可以进行HMM模型参数估计、相应的概率计算,详细原理下面展开叙述。
(1)前向后向算法
前向算法: 给定隐马尔可夫模型 λ \lambda λ, 定义到时刻t部分观测序列为 x 1 , x 2 , ⋯ ⋯ , x t x_{1}, x_{2}, \cdots \cdots, x_{t} x1,x2,⋯⋯,xt, 且状态为 i的概率为前向概率, 记作:
α t ( i ) = P ( x 1 , x 2 , ⋯ , x t , i t = i ∣ λ ) \alpha_{t}(i)=P\left(x_{1}, x_{2}, \cdots, x_{t}, i_{t}=i \mid \lambda\right) αt(i)=P(x1,x2,⋯,xt,it=i∣λ)
后向算法: 给定隐马尔可夫模型 λ \lambda λ, 定义到时刻t部分观测序列为 x 1 , x 2 , ⋯ ⋯ , x t \mathrm{x}_{1}, \mathrm{x}_{2}, \cdots \cdots, \mathrm{x}_{t} x1,x2,⋯⋯,xt, 且状态为 i \mathrm{i} i 的概率为后向概率, 记作
β t ( i ) = P ( x t + 1 , x t + 2 , ⋯ , x T ∣ i t = i , λ ) \beta_{t}(i)=P\left(x_{t+1}, x_{t+2}, \cdots, x_{T} \mid i_{t}=i, \lambda\right) βt(i)=P(xt+1,xt+2,⋯,xT∣it=i,λ)
为避免计算过程中数值的上溢与下溢, 作如下处理, 令:
S α , t = 1 max i α t ( i ) , S β , t = 1 max i β t ( i ) α t ( i ) = S α , t α t ( i ) , β t ( i ) = S β , t β t ( i ) \begin{aligned} S_{\alpha, t} &=\frac{1}{\max _{i} \alpha_{t}(i)}, S_{\beta, t}=\frac{1}{\max _{i} \beta_{t}(i)} \\ \alpha_{t}(i) &=S_{\alpha, t} \alpha_{t}(i), \beta_{t}(i)=S_{\beta, t} \beta_{t}(i) \end{aligned} Sα,tαt(i)=maxiαt(i)1,Sβ,t=maxiβt(i)1=Sα,tαt(i),βt(i)=Sβ,tβt(i)
(2)概率计算
推导可知, 给定模型 λ \lambda λ 和观测 O O O, 在时刻 t t t 处于i的概率记为:
γ t ( i ) = α t ( i ) β t ( i ) ∑ j α t ( j ) β t ( j ) \gamma_{t}(i)=\frac{\alpha_{t}(i) \beta_{t}(i)}{\sum_{j} \alpha_{t}(j) \beta_{t}(j)} γt(i)=∑jαt(j)βt(j)αt(i)βt(i)
给定模型 λ \lambda λ 和观测 O O O, 在时刻 t t t 处于状态i且在时刻 t + 1 \mathrm{t}+1 t+1 处于状态 j \mathrm{j} j 的概率记为:
γ t , t + 1 ( i , j ) = α t ( i ) P ( j ∣ i ) β t + 1 ( j ) P ( x t + 1 ∣ j ) ∑ k , l α t ( k ) P ( l ∣ k ) β t + 1 ( l ) P ( x t + 1 ∣ l ) \gamma_{t, t+1}(i, j)=\frac{\alpha_{t}(i) P(j \mid i) \beta_{t+1}(j) P\left(\boldsymbol{x}_{t+1} \mid j\right)}{\sum_{k, l} \alpha_{t}(k) P(l \mid k) \beta_{t+1}(l) P\left(\boldsymbol{x}_{t+1} \mid l\right)} γt,t+1(i,j)=∑k,lαt(k)P(l∣k)βt+1(l)P(xt+1∣l)αt(i)P(j∣i)βt+1(j)P(xt+1∣j)
(3)对数似然函数
在利用最大似然对HMM模型进行参数估计的时候,其对数似然函数如下:
L = log P ( O ∣ λ ) = log ∑ i = 1 N α T ( i ) \begin{aligned} L &=\log P(O \mid \lambda) \\ &=\log \sum_{i=1}^{N} \alpha_{T}(i) \end{aligned} L=logP(O∣λ)=logi=1∑NαT(i)
因为每次进行了归一化:
α t ( i ) = S α , t ⋅ α t ( i ) \alpha_{t}(i)=S_{\alpha, t} \cdot \alpha_{t}(i) αt(i)=Sα,t⋅αt(i)
递推到T时,可得:
α T ( i ) = S α , 1 ⋅ S α , 2 ⋯ S α , T ⋅ α T ( i ) \alpha_{T}(i)=S_{\alpha, 1} \cdot S_{\alpha, 2} \cdots S_{\alpha, T} \cdot \alpha_{T}(i) αT(i)=Sα,1⋅Sα,2⋯Sα,T⋅αT(i)
故最终对数似然函数为:
L = log P ( O ∣ λ ) = log ∑ i = 1 N α T ( i ) = log ∑ i = 1 N α T ( i ) Π i = 1 T S α , i = log ∑ i = 1 N α T ( i ) − ∑ i = 1 T log S α , i \begin{aligned} L &=\log P(O \mid \lambda) \\ &=\log \sum_{i=1}^{N} \alpha_{T}(i) \\ &=\log \sum_{i=1}^{N} \frac{\alpha_{T}(i)}{\Pi_{i=1}^{T} S_{\alpha, i}} \\ &=\log \sum_{i=1}^{N} \alpha_{T}(i)-\sum_{i=1}^{T} \log S_{\alpha, i} \end{aligned} L=logP(O∣λ)=logi=1∑NαT(i)=logi=1∑NΠi=1TSα,iαT(i)=logi=1∑NαT(i)−i=1∑TlogSα,i
(4)Baum-Welch算法
模型参数的学习问题,即给定观测序列 O = { O 1 , O 2 , … , O T } O=\{O_1,O_2,…,O_T\} O={O1,O2,…,OT},估计模型 λ = ( A , B , π ) λ=(A,B,\pi) λ=(A,B,π)的参数,对HMM模型参数的估计可以由监督学习和非监督学习的方法实现,而Baum-Welch算法是监督学习的方法。Baum-Welch算法是EM算法在隐马尔可夫模型学习中的具体实现, 由BW算法可推知隐马尔可夫模型的参数递推表达式:
- 初始状态概率向量: π ( i ) = ∑ X γ 1 X ( i ) ∑ X 1 \pi(i)=\frac{\sum_{X} \gamma_{1}^{X}(i)}{\sum_{X} 1} π(i)=∑X1∑Xγ1X(i)
- 状态转移概率矩阵: P ( j ∣ i ) = ∑ t = 1 T − 1 γ t , t + 1 ( i , j ) ∑ t = 1 T − 1 γ t ( i ) P(j \mid i)=\frac{\sum_{t=1}^{T-1} \gamma_{t, t+1}(i, j)}{\sum_{t=1}^{T-1} \gamma_{t}(i)} P(j∣i)=∑t=1T−1γt(i)∑t=1T−1γt,t+1(i,j)
- 观测概率矩阵:
μ i = ∑ t γ t ( i ) x t ∑ t γ t ( i ) , Σ i = ∑ t γ t ( i ) ( x t − μ i ) ( x t − μ i ) T ∑ t γ t ( i ) \boldsymbol{\mu}_{i}=\frac{\sum_{t} \gamma_{t}(i) \boldsymbol{x}_{t}}{\sum_{t} \gamma_{t}(i)}, \Sigma_{i}=\frac{\sum_{t} \gamma_{t}(i)\left(\boldsymbol{x}_{t}-\mu_{i}\right)\left(\boldsymbol{x}_{t}-\mu_{i}\right)^{T}}{\sum_{t} \gamma_{t}(i)} μi=∑tγt(i)∑tγt(i)xt,Σi=∑tγt(i)∑tγt(i)(xt−μi)(xt−μi)T
通过前后向算法可以得到相应的概率值,然后将相应的概率值代入上面的递推表达式,进行迭代便可以得到HMM模型的参数。
(5)预测下一个观测值
由 α t ( i ) \alpha_{\mathrm{t}}(i) αt(i) 的定义, 给定观测序列 x 1 : t \boldsymbol{x}_{1: t} x1:t, 状态为 i \mathrm{i} i 的概率为:
P ( i ∣ x 1 : t ) = α t ( i ) ∑ j α t ( j ) P\left(i \mid \boldsymbol{x}_{1: t}\right)=\frac{\alpha_{t}(i)}{\sum_{j} \alpha_{t}(j)} P(i∣x1:t)=∑jαt(j)αt(i)
则给定观测序列 x 1 : t , t + 1 x_{1: t}, t+1 x1:t,t+1 时刻伏态为 j \mathrm{j} j 的概率为: ∑ i P ( i ∣ x 1 : t ) P ( j ∣ i ) \sum_{i} P\left(i \mid \boldsymbol{x}_{1: t}\right) P(j \mid i) ∑iP(i∣x1:t)P(j∣i), 从而由全概率公式, t + 1 t+1 t+1 时刻观测值为 x t + 1 \boldsymbol{x}_{\boldsymbol{t}+1} xt+1 的概率为:
P ( x t + 1 ∣ x 1 : t ) = ∑ j P ( x ∣ j ) ∑ i P ( i ∣ x 1 : t ) P ( j ∣ i ) P\left(\boldsymbol{x}_{t+1} \mid \boldsymbol{x}_{1: t}\right)=\sum_{j} P(\boldsymbol{x} \mid j) \sum_{i} P\left(i \mid \boldsymbol{x}_{1: t}\right) P(j \mid i) P(xt+1∣x1:t)=j∑P(x∣j)i∑P(i∣x1:t)P(j∣i)
由最小均方误差估计(MMSE), 可得 t + 1 t+1 t+1 时刻观测值 x t + 1 x_{t+1} xt+1 的估计值为:
x ^ t + 1 = E [ x t + 1 ∣ x 1 : t ] \hat{\boldsymbol{x}}_{t+1}=E\left[\boldsymbol{x}_{t+1} \mid \boldsymbol{x}_{1: t}\right] x^t+1=E[xt+1∣x1:t]
即:
x ^ t + 1 = ∑ i P ( i ∣ x 1 : t ) ∑ j P ( j ∣ i ) E ( x ∣ j ) \hat{\boldsymbol{x}}_{t+1}=\sum_{i} P\left(i \mid \boldsymbol{x}_{1: t}\right) \sum_{j} P(j \mid i) E(\boldsymbol{x} \mid j) x^t+1=i∑P(i∣x1:t)j∑P(j∣i)E(x∣j)
(6)Kmeans参数初始化
在利用HMM可夫模型进行建模的过程中,我们发现模型对参数的初始化十分敏感,不同的初始化最后得到的模型效果差异非常的,经过不同的方法尝试,我们发现利用Kmeans的方法对模型进行初始化,效果非常好。利用Kmeans初始化的步骤如下:
- 选定HMM模型隐状态数n
- 将股票收盘价数据聚为n类
- 令模型参数中观测矩阵的初始均值=聚类中心的值
二、Python代码分析
Github上的hmm.py文件实现了一个高斯隐马尔可夫模型(Gaussian Hidden Markov Model, GaussianHMM)用于时间序列数据的建模和预测。模型通过EM算法(Baum-Welch算法)进行参数估计,并包含前向后向算法、预测和解码等功能,主要函数和方法如下。
(1)高斯分布函数
def gauss2D(x, mean, cov):z = -np.dot(np.dot((x-mean).T,inv(cov)),(x-mean))/2.0temp = pow(sqrt(2.0*pi),len(x))*sqrt(det(cov))return (1.0/temp)*exp(z)
该函数计算二元高斯分布的概率密度。输入为样本点x,均值mean和协方差矩阵cov。
(2)GaussianHMM 类
1 初始化
class GaussianHMM:def __init__(self, n_state=1, x_size=1, iter=20, if_kmeans=True):self.n_state = n_stateself.x_size = x_sizeself.start_prob = np.ones(n_state) * (1.0 / n_state)self.transmat_prob = np.ones((n_state, n_state)) * (1.0 / n_state)self.trained = Falseself.n_iter = iterself.observe_mean = np.zeros((n_state, x_size))self.observe_vars = np.zeros((n_state, x_size, x_size))for i in range(n_state): self.observe_vars[i] = np.random.randint(0,10)self.kmeans = if_kmeans
该函数初始化HMM模型的参数,包括隐状态数n_state、输入维度x_size、EM算法迭代次数iter、是否使用KMeans进行初始化if_kmeans等。
2 K-means参数初始化
def _init(self, X):mean_kmeans = cluster.KMeans(n_clusters=self.n_state)mean_kmeans.fit(X)if self.kmeans:self.observe_mean = mean_kmeans.cluster_centers_print("聚类初始化成功!")else:self.observe_mean = np.random.randn(self.n_state, 1) * 2print("随机初始化成功!")for i in range(self.n_state):self.observe_vars[i] = np.cov(X.T) + 0.01 * np.eye(len(X[0]))
通过K-means聚类方法对观测矩阵的均值进行初始化,并计算协方差矩阵。
3 前向算法
def forward(self, X):X_length = len(X)alpha = np.zeros((X_length, self.n_state))alpha[0] = self.observe_prob(X[0]) * self.start_probS_alpha = np.zeros(X_length)S_alpha[0] = 1 / np.max(alpha[0])alpha[0] = alpha[0] * S_alpha[0]for i in range(X_length):if i == 0:continuealpha[i] = self.observe_prob(X[i]) * np.dot(alpha[i - 1], self.transmat_prob)S_alpha[i] = 1 / np.max(alpha[i])if S_alpha[i] == 0:continuealpha[i] = alpha[i] * S_alpha[i]return alpha, S_alpha
计算前向概率,并进行归一化处理,防止数值上溢或下溢。
4 后向算法
def backward(self, X):X_length = len(X)beta = np.zeros((X_length, self.n_state))beta[X_length - 1] = np.ones((self.n_state))S_beta = np.zeros(X_length)S_beta[X_length - 1] = np.max(beta[X_length - 1])beta[X_length - 1] = beta[X_length - 1] / S_beta[X_length - 1]for i in reversed(range(X_length)):if i == X_length - 1:continuebeta[i] = np.dot(beta[i + 1] * self.observe_prob(X[i + 1]), self.transmat_prob.T)S_beta[i] = np.max(beta[i])if S_beta[i] == 0:continuebeta[i] = beta[i] / S_beta[i]return beta
计算后向概率,并进行归一化处理。
5 观测概率计算
def observe_prob(self, x):prob = np.zeros((self.n_state))for i in range(self.n_state):prob[i] = gauss2D(x, self.observe_mean[i], self.observe_vars[i])return prob
计算当前观测值在各个隐状态下的观测概率。
6 Baum-Welch算法
def train(self, X):self.trained = TrueX_length = len(X)self._init(X)print("开始训练")start_time = time.time()self.L = []for _ in tqdm(range(self.n_iter)):alpha, S_alpha = self.forward(X)beta = self.backward(X)L = np.log(np.sum(alpha[-1])) - np.sum(np.log(S_alpha))self.L.append(L)post_state = alpha * beta / (np.sum(alpha * beta, axis=1)).reshape(-1, 1)post_adj_state = np.zeros((self.n_state, self.n_state))for i in range(X_length):if i == 0:continuenow_post_adj_state = np.outer(alpha[i - 1], beta[i] * self.observe_prob(X[i])) * self.transmat_probpost_adj_state += now_post_adj_state / np.sum(now_post_adj_state)self.start_prob = post_state[0] / np.sum(post_state[0])for k in range(self.n_state):self.transmat_prob[k] = post_adj_state[k] / np.sum(post_adj_state[k])self.observe_prob_updated(X, post_state)total_time = time.time() - start_timeprint(f"训练完成,耗时:{round(total_time, 2)}sec")
通过Baum-Welch算法进行模型参数的估计。包括E步骤(计算前向后向概率和后验概率)和M步骤(更新模型参数)。
7 预测
def predict(self, origin_X, t):X = origin_X[:t]alpha, _ = self.forward(X)post_state = alpha / (np.sum(alpha, axis=1)).reshape(-1, 1)now_post_state = post_statex_pre = 0for state in range(self.n_state):p_state = now_post_state[:, state]temp = 0for next_state in range(self.n_state):temp += self.observe_mean[next_state] * self.transmat_prob[state][next_state]x_pre += p_state * tempreturn x_pre
预测时刻t的观测值。
8 预测更多时刻
def predict_more(self, origin_X, t):X = origin_X.copy()X_length = len(X)while X_length < t:alpha, _ = self.forward(X)post_state = alpha / (np.sum(alpha, axis=1)).reshape(-1, 1)now_post_state = post_statex_pre = 0for state in range(self.n_state):p_state = now_post_state[:, state]temp = 0for next_state in range(self.n_state):temp += self.observe_mean[next_state] * self.transmat_prob[state][next_state]x_pre += p_state * tempX = np.concatenate([X, x_pre[-1].reshape(-1, 1)])X_length += 1return X
预测更多时刻的观测值。
9 解码
def decode(self, X):X_length = len(X)state = np.zeros(X_length)pre_state = np.zeros((X_length, self.n_state))max_pro_state = np.zeros((X_length, self.n_state))max_pro_state[0] = self.observe_prob(X[0]) * self.start_probfor i in range(X_length):if i == 0:continuefor k in range(self.n_state):prob_state = self.observe_prob(X[i])[k] * self.transmat_prob[:, k] * max_pro_state[i - 1]max_pro_state[i][k] = np.max(prob_state)pre_state[i][k] = np.argmax(prob_state)state[X_length - 1] = np.argmax(max_pro_state[X_length - 1, :])for i in reversed(range(X_length)):if i == X_length - 1:continuestate[i] = pre_state[i + 1][int(state[i + 1])]return state
利用维特比算法解码观测序列,求其最可能的隐藏状态序列。
(3)总结
该代码实现了一个功能完备的高斯隐马尔可夫模型(GaussianHMM),包括初始化、前向后向算法、Baum-Welch算法进行参数估计、预测和解码等功能。通过K-means聚类进行初始化可以提高模型的初始参数设置,从而提高模型的训练效果。
三、实验分析
(1)对股票指数建模的模型参数
以DJ指数的收盘价为观测序列, 隐状态数量states分别设为 4 , 8 , 16 , 32 4,8,16,32 4,8,16,32, 我们得到了不同情况下的HMM模型, 其中以states = 8 =8 =8 为例, 学习得到的参数为:
初始概率分布: ( 0.000044 0.000000 0.000000 0.000000 0.000000 0.000000 0.999956 ) (\begin{array}{lllllll}0.000044 & 0.000000 & 0.000000 & 0.000000 & 0.000000 & 0.000000 &0.999956\end{array}) (0.0000440.0000000.0000000.0000000.0000000.0000000.999956)
状态转移概率矩阵: ( 0.9498 0 0 0 0 0 0.0317 0.0185 0 0.9729 0 0 0.0158 0.0113 0 0 0 0 0.9433 0 0 0.0205 0.0362 0 0 0 0 0.9923 0.0077 0 0 0 0 0.0338 0 0.0178 0.9484 0 0 0 0 0.0091 0.0136 0 0 0.9773 0 0 0.0242 0 0.0296 0 0 0 0.9462 0 0.0238 0 0 0 0 0 0 0.9762 ) \left(\begin{array}{rrrrrrrr}0.9498 & 0 & 0 & 0 & 0 & 0 & 0.0317 & 0.0185 \\ 0 & 0.9729 & 0 & 0 & 0.0158 & 0.0113 & 0 & 0 \\ 0 & 0 & 0.9433 & 0 & 0 & 0.0205 & 0.0362 & 0 \\ 0 & 0 & 0 & 0.9923 & 0.0077 & 0 & 0 & 0 \\ 0 & 0.0338 & 0 & 0.0178 & 0.9484 & 0 & 0 & 0 \\ 0 & 0.0091 & 0.0136 & 0 & 0 & 0.9773 & 0 & 0 \\ 0.0242 & 0 & 0.0296 & 0 & 0 & 0 & 0.9462 & 0 \\ 0.0238 & 0 & 0 & 0 & 0 & 0 & 0 & 0.9762\end{array}\right) 0.9498000000.02420.023800.9729000.03380.009100000.9433000.01360.029600000.99230.017800000.015800.00770.948400000.01130.0205000.9773000.031700.03620000.946200.01850000000.9762
观测概率分布:
-
均值: ( 12519.93 9640.24 10388.37 13541.56 13009.42 12052.83 8276.14 11241.26 ) (\begin{array}{llllllll}12519.93 & 9640.24 & 10388.37 & 13541.56 & 13009.42 & 12052.83 & 8276.14 & 11241.26\end{array}) (12519.939640.2410388.3713541.5613009.4212052.838276.1411241.26)
-
协方差: ( 23834.89 71700.85 45532.26 57449.12 26262.64 28852.07 338454.89 68110.31 ) (23834.89 \quad 71700.85 \quad 45532.26 \quad 57449 .12 \quad 26262.64 \quad 28852.07 \quad 338454.89 \quad 68110 .31) (23834.8971700.8545532.2657449.1226262.6428852.07338454.8968110.31)
我们可以看到模型最终参数中观测概率分布中的均值和一开始聚类初始化的均值十分接近,这也是为什么Kmeans均值初始化效果非常好的原因。
(2)不同states下的对数似然变化
不同states下的对数似然变化情况如下图所示:
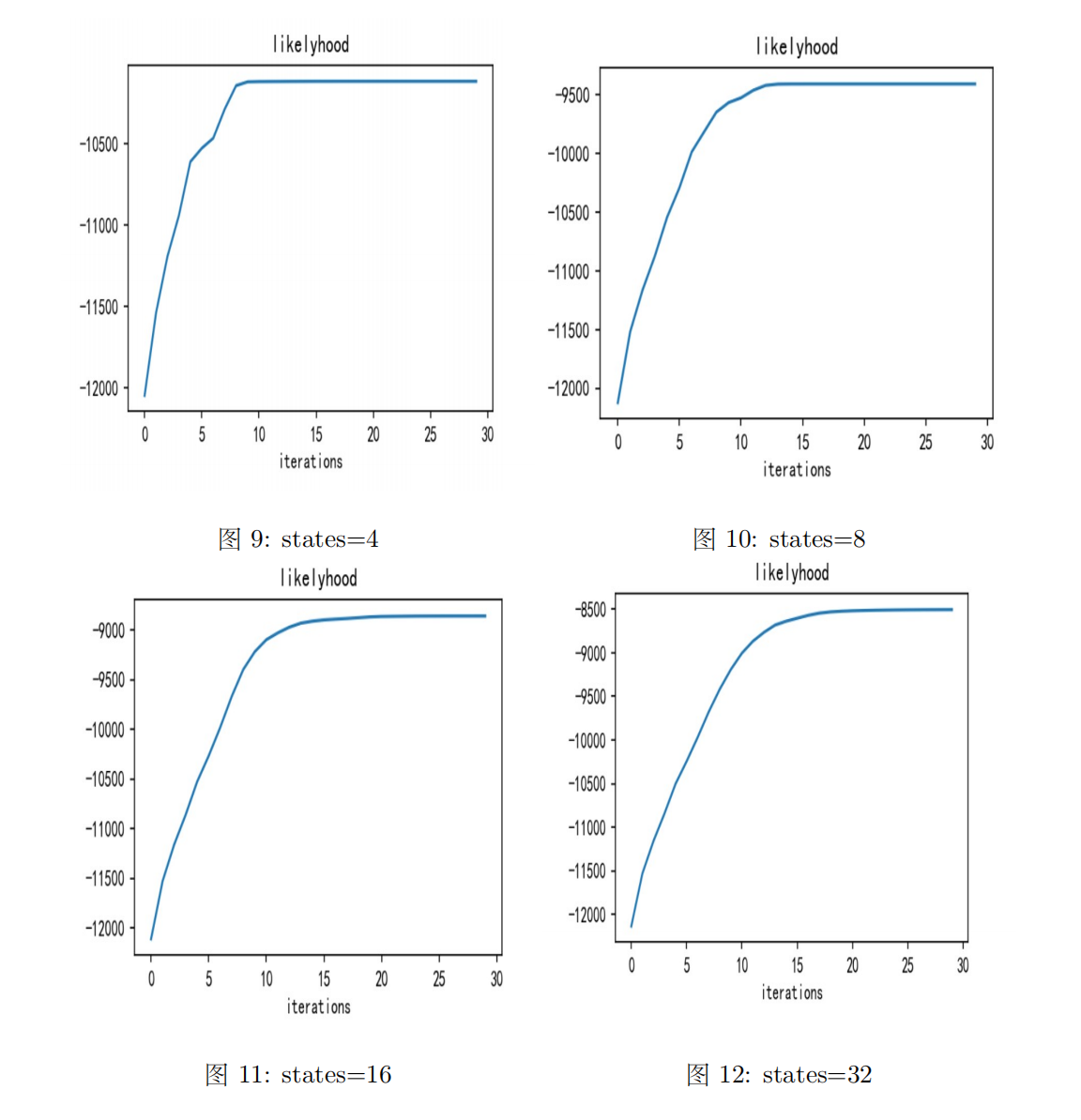
我们可以看到随着迭代次数的增加,对数似然越来越大,说明模型拟合效果越来越好。并且隐状态数目越多,最终对数似然函数值也越大,说明隐状态越多,模型效果越好。
(3)不同states下的股票指数拟合效果
不同states下的股票指数拟合效果如下图所示:
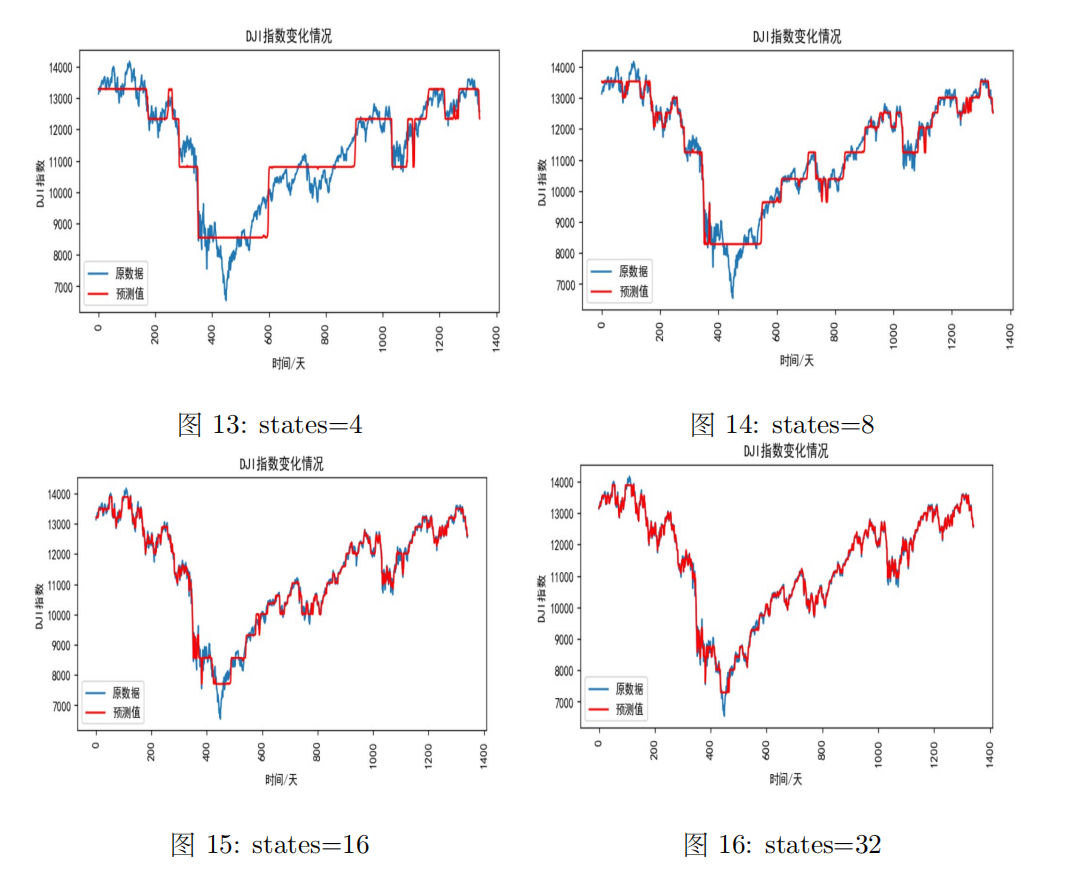
由上面不同隐状态下模型拟合效果图可知,states数越多,模型拟合效果越好,但是需要根据BIC和AIC准则以及训练模型的代价以及是否过拟合等方面来进行模型选择。
(4)不同states下的误差及MSE
不同states下的误差及MSE如下图所示:
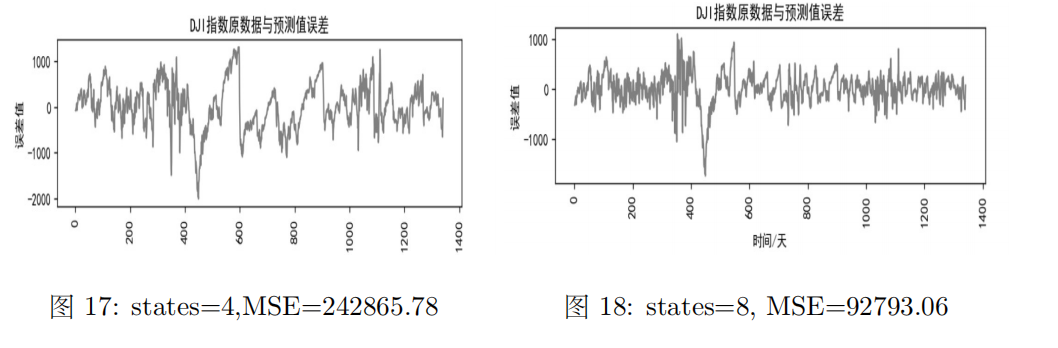
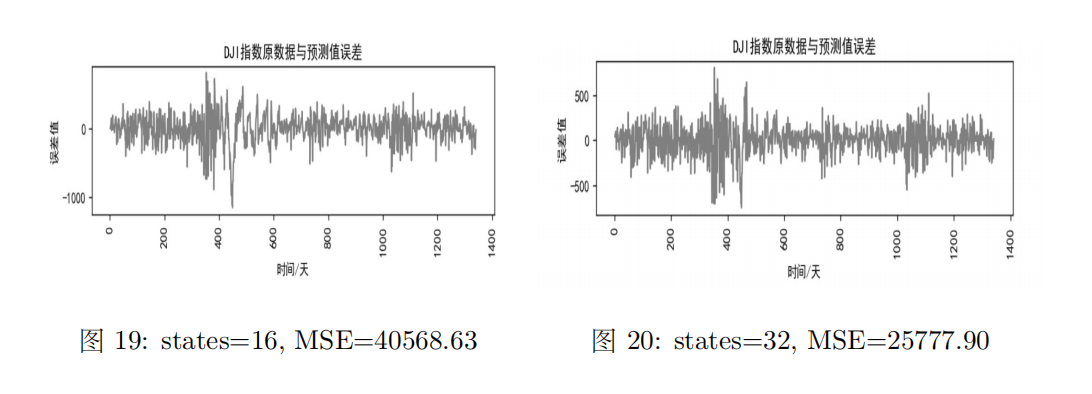
观察图中数据可知,states数越多,绝对误差与MSE越小,说明拟合效果越好。
(5)HMM模型单支股票预测小结
以DJI指数的收盘价为观测序列,隐状态数量states分别设为4,8,16,32,我们得到了不同情况下的HMM模型,并比较了训练所消耗时间,训练结果的AIC、BIC预测结果的平均误差、均方误差,结果如下表所示:
| States | Train Times | AIC | BIC | Mean Error | MSE |
|---|---|---|---|---|---|
| 4 | 25.84 sec | 20237.65 | 20258.46 | 384.13 | 242865.78 |
| 8 | 46.93 sec | 18827.66 | 18869.28 | 217.18 | 92793.06 |
| 16 | 78.43 sec | 17752.77 | 17836.00 | 145.24 | 40568.63 |
| 32 | 147.48 sec | 17074.84 | 17241.30 | 114.51 | 25777.90 |
我们可以看到随着隐状态数的增加:
- 模型的拟合误差不断减小
- AIC和BIC指数不断上升
- 对数似然也越来越大
- 但是模型训练时间也成倍上升
所以在实际应用的过程中,我们需要考虑模型越复杂带来提升的效果和代价,并且在两者之间找到一个权衡,而在后面的对比分析中,我们便采用的是隐状态数=16。(关于AIC和BIC的介绍可以看我这篇文章——时间序列分析入门:概念、模型与应用【ARMA、ARIMA模型】。
(6)多支股票训练模型
在前面的分析中,我们是对单只股票或者股票指数进行HMM建模,但事实上可以利用HMM对多只股票进行建模,这时多只股票共用同一个HMM参数和隐状态序列,我们以AAPL单支股票训练HMM模型得到如下结果:

可以看到单只股票建模相对误差率为3.1%,我们以AAPL与BAC、AAPL与C为例训练模型,得到的预测效果如下图所示:
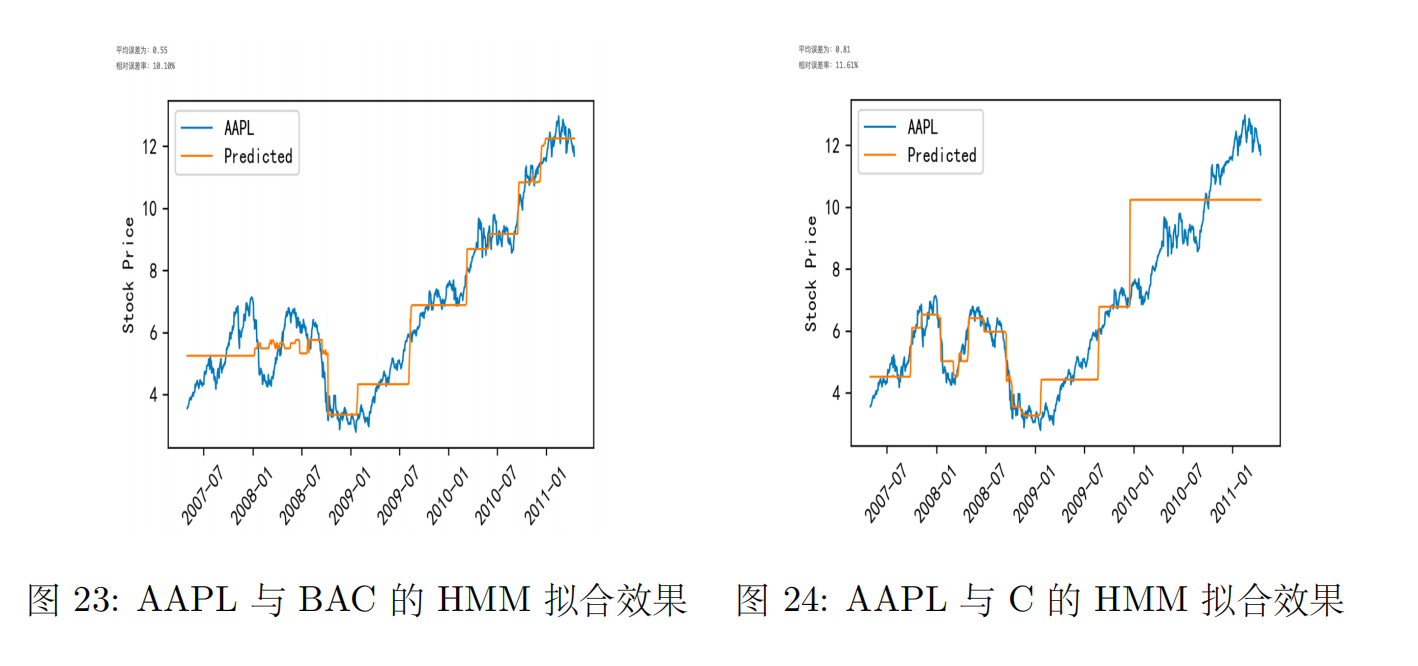
观察上两图知,多支股票数据训练出来的模型效果不如单支股票的效果,且由相关性分析知,相关性越大的两支股票组成的数据训练出的模型有更好的预测效果。不过这里面的原因可能比较复杂,有可能有负迁移的影响,不相关的股票数据导致共同建模效果反而不好。










![【代码随想录】【算法训练营】【第49天】 [300]最长递增子序列 [674]最长连续递增序列 [718]最长重复子数组](https://img-blog.csdnimg.cn/direct/2bb6e7a5febb4176a93489a8aad5b5e0.png)