最小生成树(Minimum Spanning Tree)

(1)概念

我们知道，树是有$n$个结点，$n-1$条边的无向无环的连通图。

一个连通图的生成树是一个极小的连通子图，它包含图中全部的$n$个顶点，但只有构成一棵树的$n-1$条边。

最小生成树就是一个带权图，每个边都有一个边权，一颗生成树的权值是该树边所有边权的和，$MST$就是所有生成树中最小的一个。

(2)Prim算法（遍历点的算法）

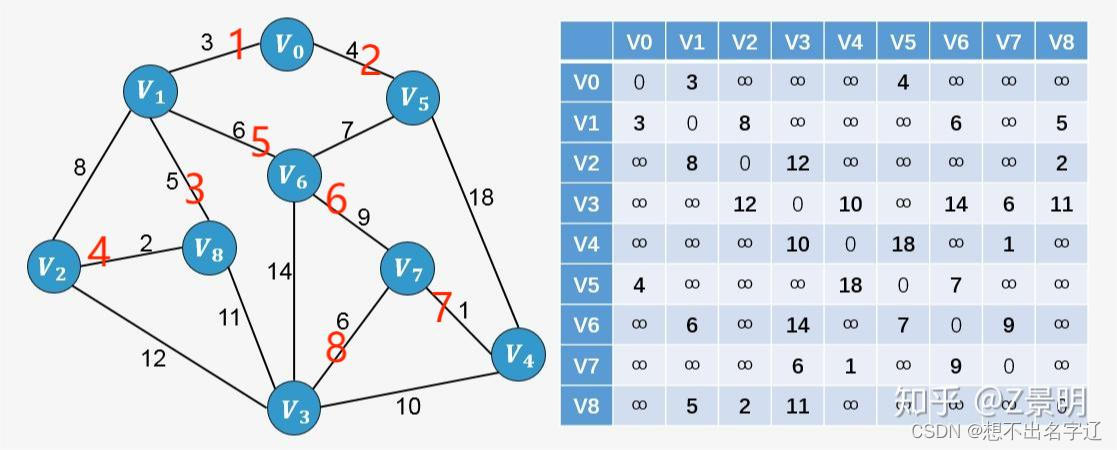
普里姆算法在找最小生成树时，将顶点分为两类，一类是在查找的过程中已经包含在生成树中的顶点（假设为 A 类），剩下的为不在生成树中的（假设为 B 类）。

对于给定的连通网，起始状态全部顶点都归为 B 类。在找最小生成树时，选定任意一个顶点作为起始点，并将之从 B 类移至 A 类；然后找出 B 类中到 A 类中的顶点之间权值最小的顶点，将之从 B 类移至 A 类，如此重复，直到 B 类中没有顶点为止。所走过的顶点和边就是该连通图的最小生成树。

int dis[N];
int mp[N][N];
bool vis[N];void work() {int n, m;cin >> n >> m;int ans = 0;memset(vis, 0, sizeof vis);memset(mp, 0x3f3f3f3f, sizeof mp);for (int i = 0; i < n; ++i) {int u, v, w;cin >> u >> v >> w;mp[u][v] = w;mp[v][u] = w;}for (int i = 0; i < n; ++i) {dis[i] = 0x3f3f3f3f;}dis[0] = 0;vis[0] = 1;for (int i = 1; i < n; ++i) {dis[i] = min(dis[i], mp[0][i]);}for (int i = 1; i < n; ++i) {//这里的外层循环是循环遍数，与i值无关double minn = 0x3f3f3f3f;int pos = -1;for (int j = 1; j < n; ++j) {//每次循环找出与已排联通块距离最近的点if (!vis[j] && minn > dis[j]) {pos = j;minn = dis[j];}}ans += minn;vis[pos] = 1;for (int j = 0; j < n; ++j) {//刷新未连接点的距离最小值dis[j] = min(dis[j], mp[pos][j]);}}cout << ans << '\n';
}

正确性显然。

复杂度是$O(n^2)$级别的，但是我们可以使用堆优化降到$O(nlogn)$，之后讲最短路的时候会讲堆优化。

(3)Kruskal算法（遍历边的算法）

克鲁斯卡尔算法（Kruskal）是一种使用贪婪方法的最小生成树算法。 该算法初始将图视为森林，图中的每一个顶点视为一棵单独的树。 一棵树只与它的邻接顶点中权值最小且不违反最小生成树属性（不构成环）的树之间建立连边。

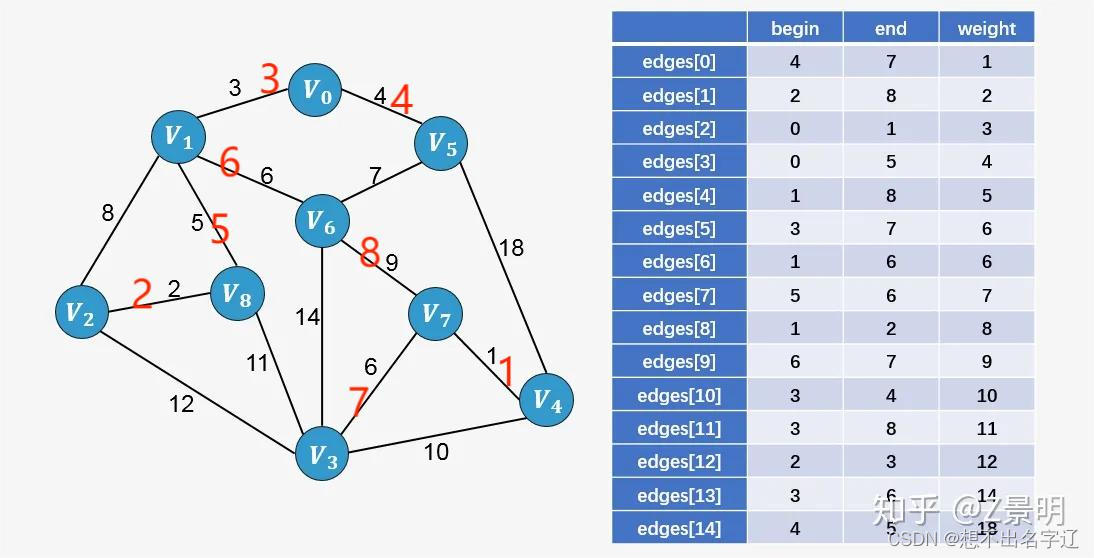
利用并查集可以快速实现查找两个点是否已经连接

int n, m;
int f[105];
struct road {int a, b, v;
} arr[305];int find(int a) {if (f[a] == a)return a;elsereturn f[a] = find(f[a]);
}void join(int a, int b) {if (find(a) != find(b))f[find(a)] = find(b);
}bool cmp(road a, road b) {return a.v < b.v;
}void work() {cin >> n >> m;int a, b, c;for (int i = 1; i <= n; ++i) {f[i] = i;}int ans = 0;for (int i = 0; i < m; ++i) {cin >> arr[i].a >> arr[i].b >> arr[i].v;}sort(arr, arr + m, cmp);//先按路的权值排序，如果两点的祖先不是一个就加上然后合并。for (int i = 0; i < m; ++i) {if (find(arr[i].a) != find(arr[i].b)) {ans += arr[i].v;join(arr[i].a, arr[i].b);}}cout << ans << '\n';return 0;
}

正确性证明：

给一带权连通的树一定会有至少一棵生成树，那么这些生成树中间必然会会存在至少一棵最小生成树。

假设$T$是用$kruskal$求出来的最小生成树，而$U$是这个图的最小生成树，要证$U=T$。
然而如果$T\ne U$，那么至少存在一条边在$T$中，不在$U$中，假设存在$k$条边存在$T$中不存在$U$中。
接下来进行$k$次变换：
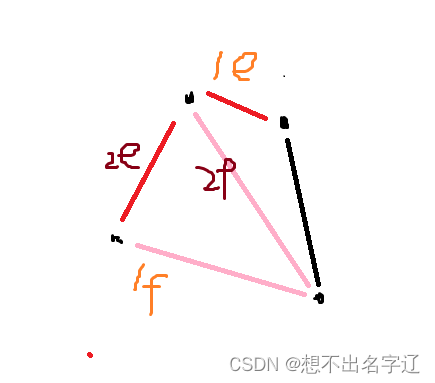
每次将在$T$中不在$U$中的最小的边$f$拿出来放到$U$中，那么$U$中必然形成一条唯一的环路，我们取出这个环路上最小的且不在$T$中的边$e$放回到$T$中，这样的边$e$一定是存在的，因为之前的$T$不存在环路（如果$e$在$T$中那么就可能和$f$形成环路）。

现在证明$f$和$e$权值的关系：

假设$f<e$,那么后来形成的$U$是权值之和更小了，与$U$是最小生成树矛盾。 实际上，不可能在$U$中拿到大于$f$的边，因为把$f$拿走后，如果小于$f$的边都不成立，至少$f$是一个符合条件的边会被那回。

假设$f>e$,那么根据$kruskal$的做法，$e$是在$f$之前被取出来的边但是被舍弃了，一定是因为$e$和比$e$小的边形成了环路，而比$e$小的边都是存在$U$中的，而$e$和这些边并没有形成环路，于假设矛盾。

于是$f$一定和$e$相等的，$k$次变换后，$T$和$U$的权值之和是相等的。

最小生成树的值也是相等的。

复杂度是$O(nlogn)$级别的，一般有mst就用这个。

int f[N];
struct road {int a, b, v;
} arr[N];
int tot = 0;int find(int a) {if (f[a] == a)  return a;return f[a] = find(f[a]);
}void join(int a, int b) {if (find(a) != find(b)) f[find(a)] = find(b);
}bool cmp(road a, road b) {return a.v < b.v;
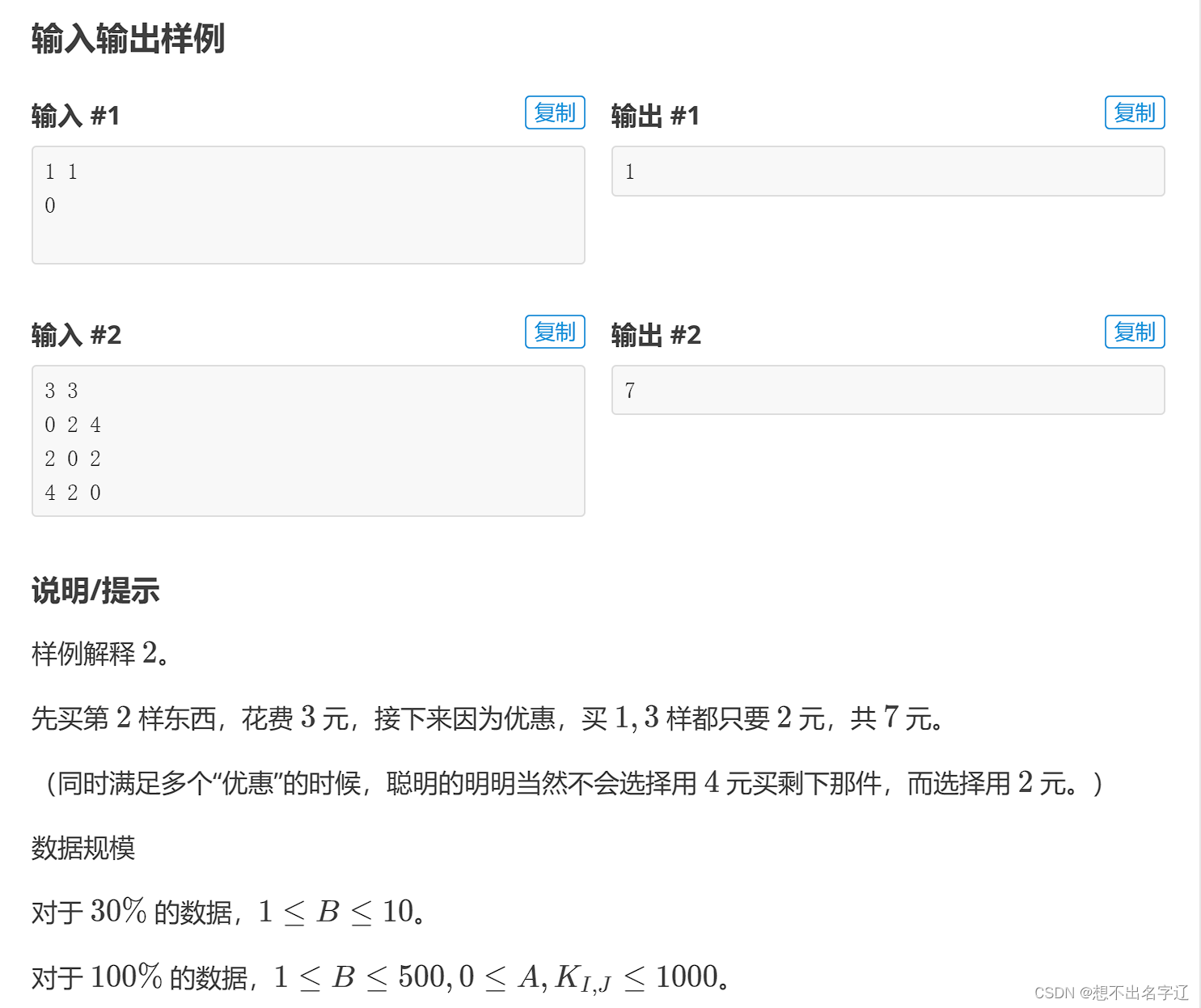
}void work() {int a, b;cin >> a >> b;for (int i = 1; i <= b; ++i) {f[i] = i;arr[i] = {0, i, a};}tot = b;for (int i = 1; i <= b; ++i) {for (int j = 1; j <= b; ++j) {int x; cin >> x;if (x == 0) continue;else arr[++tot] = {i, j, x};}}ll ans = 0;sort(arr + 1, arr + 1 + tot, cmp);for (int i = 1; i <= tot; ++i) {if (find(arr[i].a) != find(arr[i].b)) {ans += arr[i].v;join(arr[i].a, arr[i].b);b--;}if (b == 0) break;}cout << ans << '\n';
}