目录
- 前言
- 一、线性表的链式表示和实现
- 1.1 线性表的表示
- 1.2 基本操作的实现
- 1.3 线性表的链式表示的优缺点
- 总结
前言
本篇文章主要介绍线性表的链式表示
一、线性表的链式表示和实现
1.1 线性表的表示
线性表的链式表示又称为链式存储结构或链式映像
链式存储定义:逻辑上相邻的数据元素在物理存储结构中不一定相邻
线性表的链式表示是用一组物理位置任意的存储单元来存放线性表的数据元素,这组存储单元可能是连续,也可能是不连续的,取决于操作系统的分配策略。
线性表的逻辑关系使用指针表示
线性表
( a , b , c , d ) (a,b,c,d) (a,b,c,d)
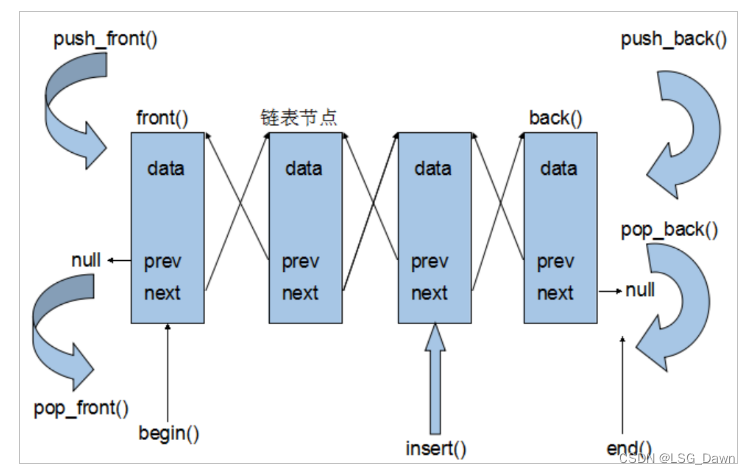
链式存储结构

一个结点由数据域和指针域组成
数据域:数据元素本身本身信息,
指针域:存储其后继结点的存储地址
一般,称指向第一个结点的指针称为链表的头指针
一般,可以将链式存储结构简化如下图表示:

单链表是由头指针唯一确定,因此单链表可以用头指针的名字来命令。
与链式存储结构有关的术语
假设有一个线性表 ( a 1 , a 2 , ⋯ , a n ) (a_1,a_2,\cdots,a_n) (a1,a2,⋯,an),其链式存储结构如下:

头指针:指向链表的第一个结点的指针
首元结点:指链表中存储第一个数据元素 a 1 a_1 a1的结点
头结点:为了便于对链表的处理,在链表的首元结点之前附加的一个结点
假设一个线性表为 ( a , b , c , d ) (a,b,c,d) (a,b,c,d)
不带头结点的链式存储结构

带头结点的链式存储结构

讨论
- 如何表示空表?
无头结点时,头指针为空时表示空表
有头结点时,当头结点的指针域为空时表示空表 - 在链表设置头结点的好处?
便于首元结点的处理
便于空表和非空表的处理
1.2 基本操作的实现
单链表的定义和表示
//定义返回值常量
#define SUCCESS 1
#define ERROR 0//假设数据元素类型为char
typedef char ElemType;//定义结点类型
struct Node;
typedef struct Node* PNode; //假设作为结点指针类型
struct Node {ElemType data; //数据域PNode next; //指针域
};typedef struct Node* LinkList; //假设作为单链表类型
为了处理方便,这是使用带头结点的链式存储结构。
下面介绍如何实现线性表的基本操作。
-
创建空链表
step1 使用malloc()函数创建一个sizeof(struct Node)大小的空间作为头结点
step2 将头结点的指针域置为NULL,表示一个空表//3.1 创建一个空链表 LinkList createNullList_link(void) {LinkList llist = (LinkList)malloc(sizeof(struct Node));if (NULL == llist){printf("malloc fail!\n");return NULL;}llist->next = NULL;return llist; } -
销毁链表
step1 首先销毁链表的数据元素结点
step2 最后销毁链表的头结点//3.2 销毁一个单链表 void destroyList_link(LinkList* linkList) {assert(linkList && *linkList);PNode p = (*linkList)->next;//1. 销毁数据元素结点while (p){PNode pnext = p->next;free(p);p = pnext;}//2. 销毁头结点free(*linkList);*linkList = NULL; } -
链表的查找
step1 判断链表是否为空表
step2 从首元结点开始查找
step3 查找失败,返回ERROR;查找成功,返回数据元素的位置序号//3.7 根据指定数据元素e获取数据元素的对应序号 int locateElem_link(LinkList linkList, ElemType e) {assert(linkList);PNode p = linkList->next; //首元结点int j = 1;while (p && p->data != e){p = p->next;j++;}if (p)return j;elsereturn ERROR; } -
链表的插入
step1 首先找到 a i − 1 的存储位置 p a_{i-1}的存储位置p ai−1的存储位置p
step2 生成一个数据域为e的新结点newNode
step3 插入新结点,即newNode的指针域指向 a i a_i ai,结点 a i − 1 a_{i-1} ai−1的指针域指向newNode

//3.8 在第i个元素之前插入数据元素e int insertElem_link(LinkList linkList, int i, ElemType e) {assert(linkList);PNode p = linkList; //考虑插入位置可能在第1个之前int j = 0;while (p && j < i - 1){p = p->next;++j;}if (!p || j > i - 1) //当 p == NULL成立时,说明i-1大于表长; j > i-1 为了应对i <= 0情况 return ERROR;//新建结点PNode newNode = (PNode)malloc(sizeof(struct Node));if (NULL == newNode){printf("malloc fail!\n");return ERROR;}newNode->data = e;newNode->next = p->next;p->next = newNode;return SUCCESS; } -
链表的删除
step1 首先找到 a i − 1 a_{i-1} ai−1的存储位置p
step2 使结点 a i − 1 a_{i-1} ai−1的指针域指向 a i + 1 a_{i+1} ai+1

//3.9 将链表第i个数据元素删除 int deleteElem_link(LinkList linkList, int i) {assert(linkList);PNode p = linkList;int j = 0;while (p->next && j < i - 1){p = p->next;j++;}if (!(p->next) || j > i - 1) //p->next,因为删除的是p->next,而不是p所指的结点return ERROR;PNode q = p->next;p->next = q->next;free(q);q = NULL;return SUCCESS; }
1.3 线性表的链式表示的优缺点
-
优点
在线性表的链式存储结构中,数据元素之间的逻辑关系靠结点的指针域来指示,结点的空间是动态申请和动态释放的,所以不需要预先按最大的需要分配连续空间;
线性表的插入和删除只需要修改指针域,而不需要移动其他数据元素 -
缺点
存储密度小,每个结点的指针域需要额外占用存储空间;
链式存储结构是一种非随机存储结构,查找任一个结点都要从头指针开始,沿着指针链一个一个地搜索,增加算法的时间代价。
总结
完整代码:https://gitee.com/PYSpring/data-structure/tree/master