一、安装
(1)进入宝塔官网
https://www.bt.cn/new/index.html
(2)点击“ 立即免费安装 ”,选择 Centos安装脚本
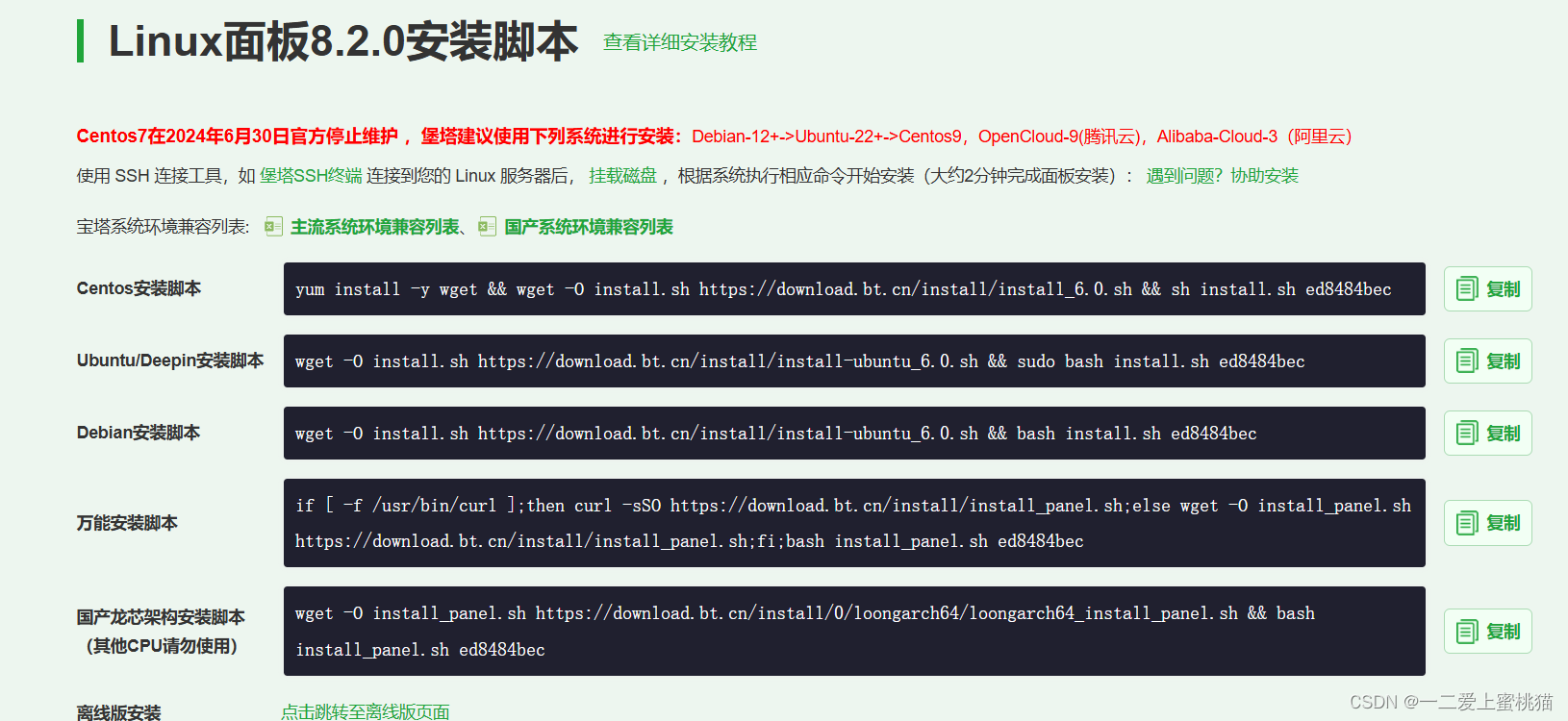
(3)进入 ssh 输入以下命令安装宝塔
yum install -y wget && wget -O install.sh https://download.bt.cn/install/install_6.0.sh && sh install.sh ed8484bec输入“y” 表示许可
注意保存外网面板地址,内网面板地址,username,password
(4)进入阿里云,依次点击“云服务器ECS”,“安全组”,“管理规则”,放行端口,端口号为面板地址冒号后面的数字
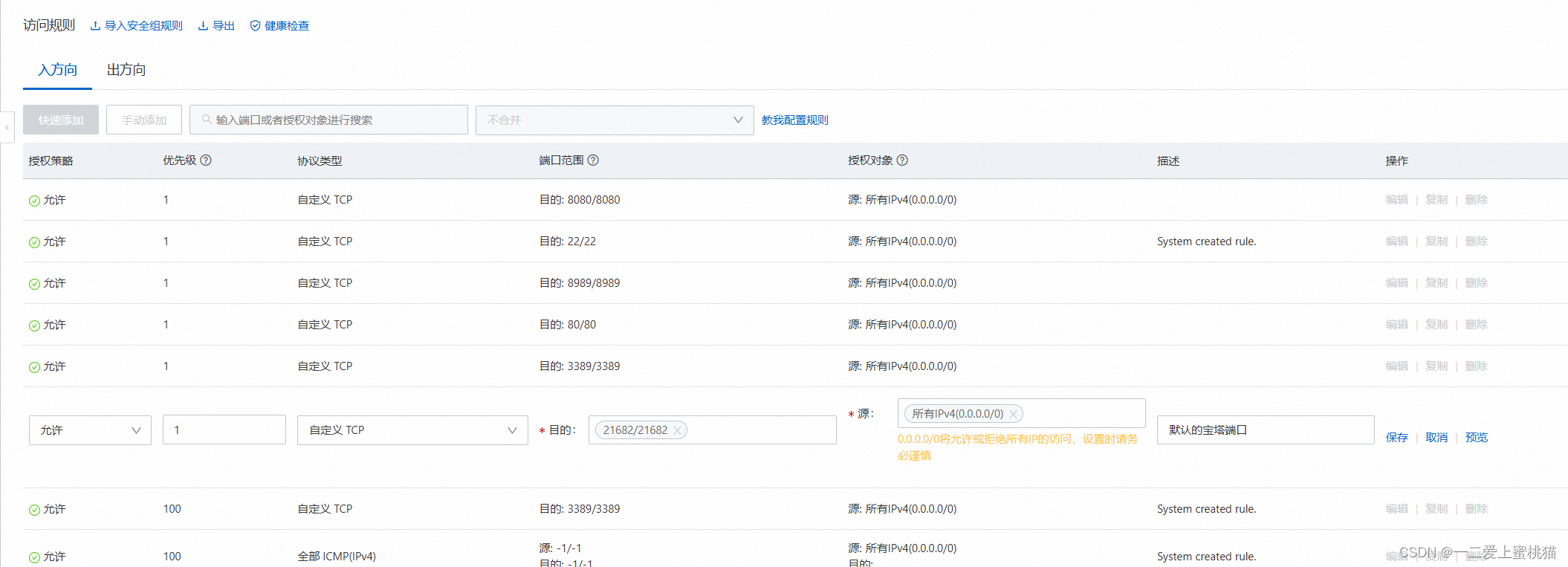
二、登录
(1)复制进入之前保存的外网面板地址
账号密码为之前保存的username和password
阅读并同意用户协议

三、配置环境
(1)绑定宝塔官网账号,没有的话可以去注册一个
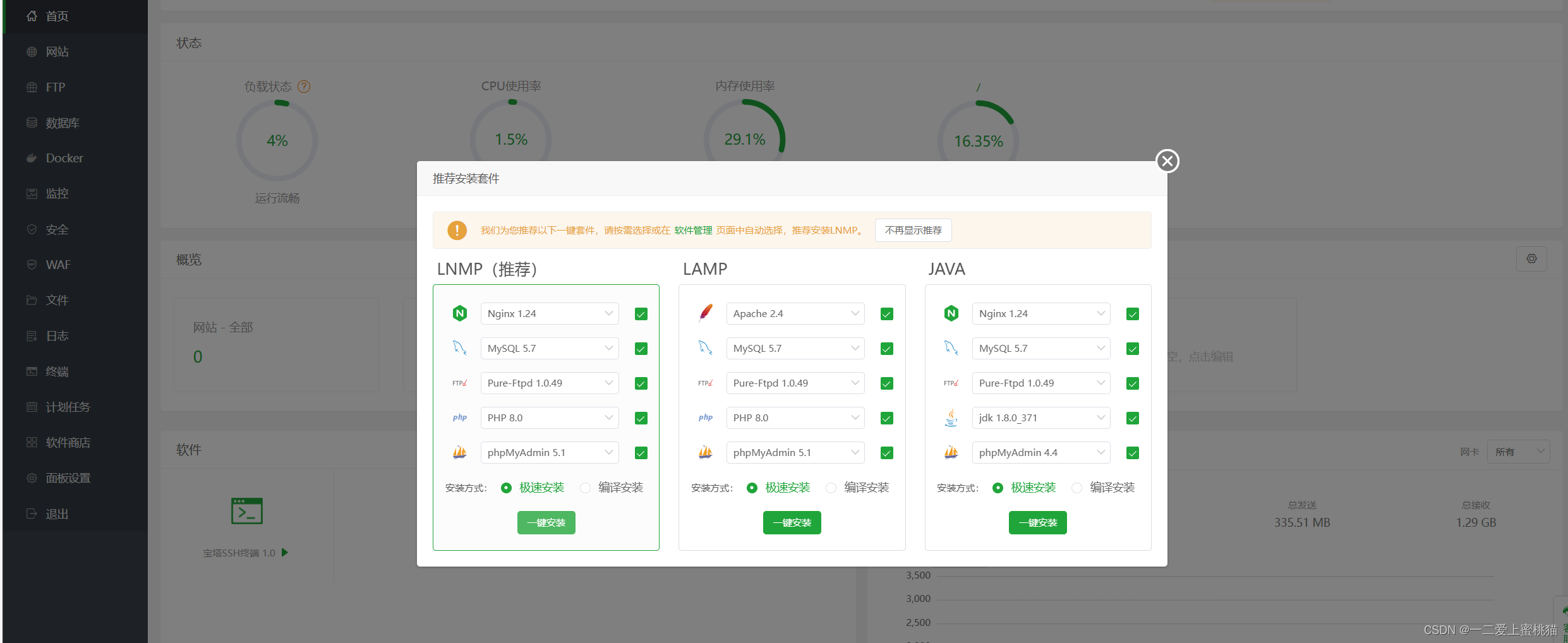
(2) 安装Wordpress要求的几个软件
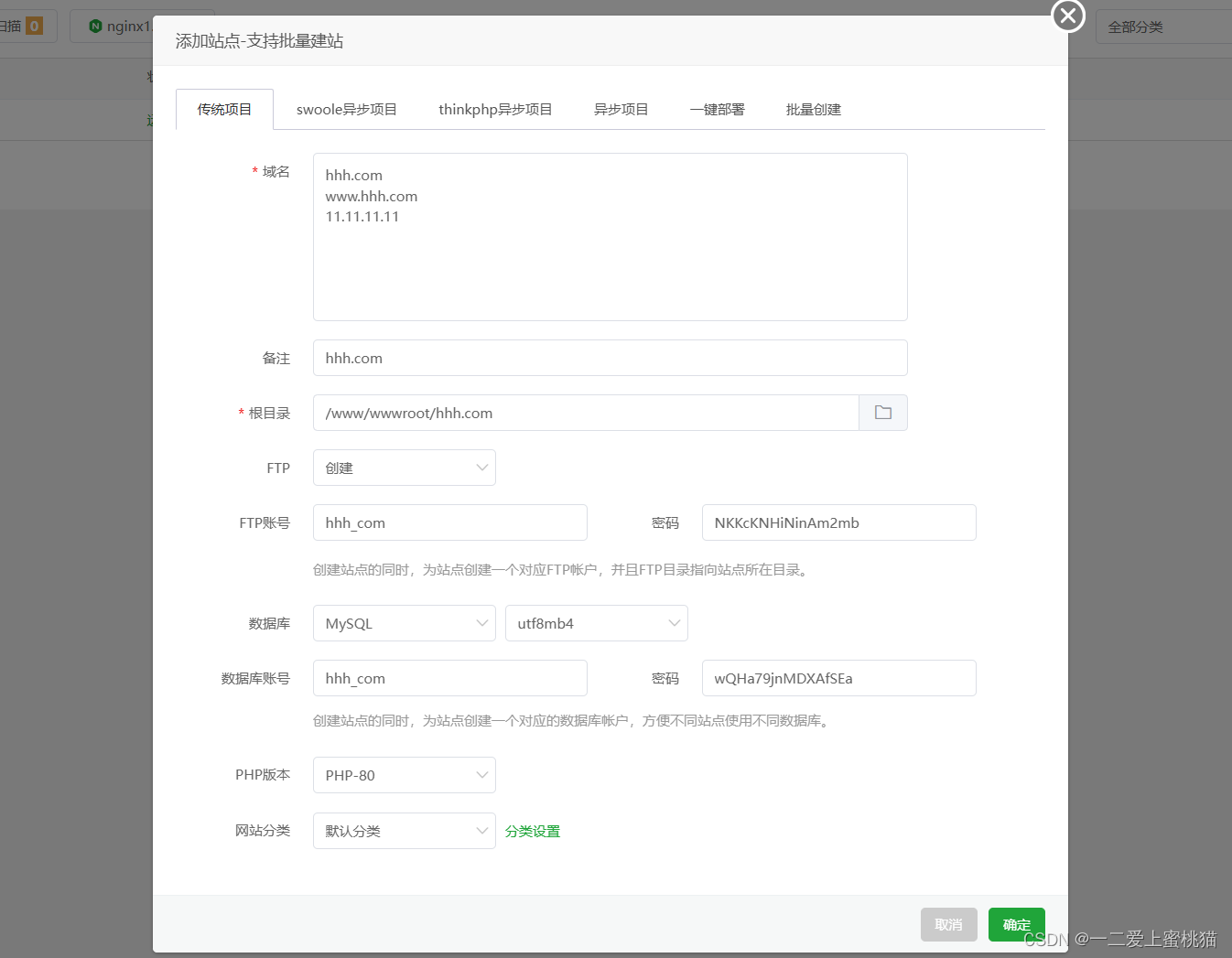
(3)点击 “网站”,添加三行域名,勾选数据库和FTP
(4)回到阿里云的安全组,开放80端口

(5) 还是在阿里云中,进行域名解析

(6) 再次进入公网IP,显示创建成功

四、卸载
(1)进入 ssh 输入以下命令下载脚本
wget http://download.bt.cn/install/bt-uninstall.sh
(2)执行脚本
sh bt-uninstall.sh