给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2 输出:[0,1,1] 解释: 0 --> 0 1 --> 1 2 --> 10
示例 2:
输入:n = 5 输出:[0,1,1,2,1,2] 解释: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101
提示:
0 <= n <= 105
进阶:
- 很容易就能实现时间复杂度为
O(n log n)的解决方案,你可以在线性时间复杂度O(n)内用一趟扫描解决此问题吗? - 你能不使用任何内置函数解决此问题吗?(如,C++ 中的
__builtin_popcount)
思路:
遍历,右移,数出每一位即可
代码:
class Solution {
public:vector<int> countBits(int n) {vector<int> res;for(int i=0;i<=n;i++){int t =0;int k=i;while(k){if(k&1)t++;k=k>>1;}res.push_back(t);}return res;}
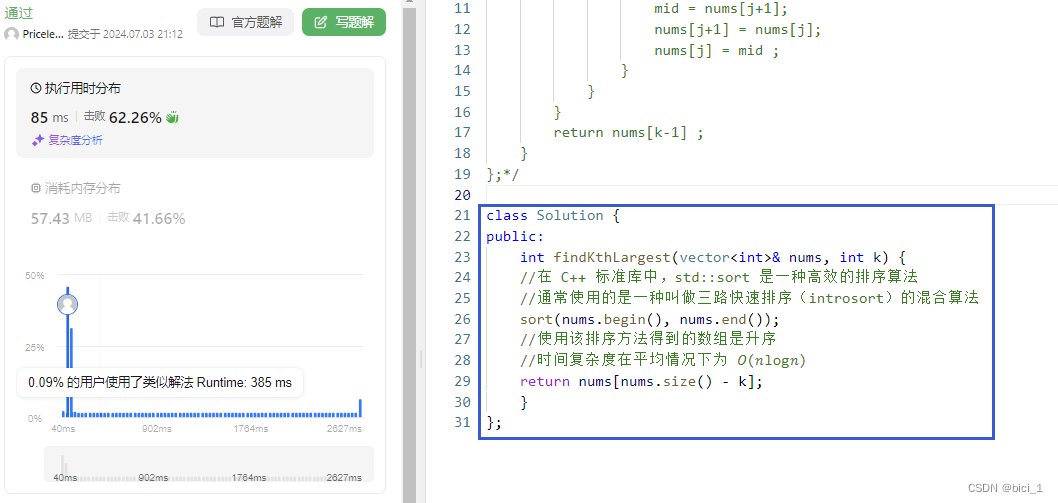
};运行结果:
可见暴力解法速度较慢












![[go-zero] 简单微服务调用](https://i-blog.csdnimg.cn/direct/b9de06b6d462431eab168ba55b2fb7d0.png)