20、matlab信号波形生成：狄利克雷函数、高斯脉冲和高斯脉冲序列

1、名词说明

狄利克雷函数（Dirac Delta Function）

狄利克雷函数，也称为单位冲激函数或δ函数，是一个在数学和信号处理中常用的特殊函数。狄利克雷函数通常用符号δ(t)表示，其定义为：

δ(t) = { +∞, t = 0{  0,  t ≠ 0

狄利克雷函数在时间 t = 0 时取无限值，而在其他时间点上取值为零。它在信号处理中常用于描述脉冲信号、冲击响应等情况，是一种理想化的脉冲函数。

高斯脉冲（Gaussian Pulse）

高斯脉冲是以高斯分布函数为基础构造的脉冲信号，其数学形式为：

g(t) = A * exp(-(t - t0)^2 / (2 * σ^2))

其中，A 是幅度参数，t0 是时间偏移参数，σ 是标准差参数。高斯脉冲在信号处理中常用于平滑滤波、调制解调、通信系统等领域，具有良好的特性和数学性质。

高斯脉冲序列（Gaussian Pulse Train）

高斯脉冲序列是由一系列高斯脉冲组成的序列，通常用于模拟通信系统中的调制信号或模拟神经信号。高斯脉冲序列在信号处理和系统建模中具有重要的应用，可以通过调节各个高斯脉冲的参数来实现不同的信号波形和频谱特性。

高斯脉冲序列的性质使其在实际应用中具有很好的可控性和适应性，广泛应用于数字通信、雷达系统、生物医学工程等领域。

2、狄利克雷函数生成波形diric()函数

diric()函数简介

在 MATLAB 中，狄利克雷函数可以通过diric()函数生成。diric()函数用于计算周期为N的狄利克雷函数的离散样本值，其语法为：

y = diric(x, N)

其中，x是自变量序列，N是周期参数。diric()函数会返回狄利克雷函数在给定序列x上的值。

下面是一个示例，演示如何使用diric()函数生成狄利克雷函数的波形：

x = 0:0.01:5; % 定义自变量序列 
N = 5; % 定义周期参数 
y = diric(2*pi*x, N); % 计算狄利克雷函数在给定序列上的值 
% 绘制狄利克雷函数波形 
plot(x, y); 
xlabel('x'); 
ylabel('diric(x, 5)'); 
title('狄利克雷函数波形');

在这个示例中，我们定义了自变量序列x和周期参数N，然后使用diric()函数计算狄利克雷函数在序列x上的值，并绘制了狄利克雷函数的波形。您可以根据需要调整自变量序列和周期参数来生成不同的狄利克雷函数波形。

语法：y = diric(x,n) 返回n次的狄利克雷函数对输入数组x的元素求值。

1）diric()函数

代码

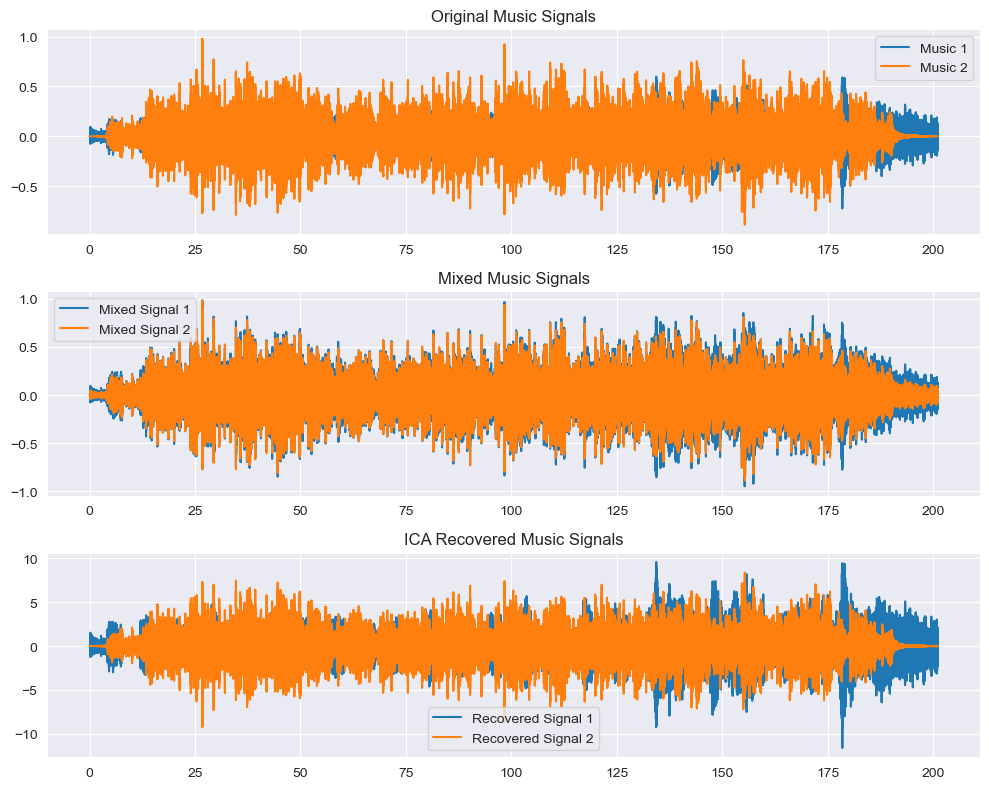
x = linspace(-2*pi,2*pi,301);%定义x取值
d6 = diric(x,6);
d7 = diric(x,7);
subplot(2,1,1)
plot(x,d6)
ylabel('n= 6')
title('狄利克雷函数')
subplot(2,1,2)
plot(x/pi,d7)
ylabel('n= 7')

视图效果

2）周期和非周期Sinc函数

代码

xm = 8;
x = linspace(-xm,xm,1001)';
n= 6;
yd = diric(x*pi,n);
ys = sinc(n*x/2)./sinc(x/2);
ys(~mod(x,2)) = (-1).^(x(~mod(x,2))/2*(n-1));
subplot(2,1,1)
plot(x,yd)
title('D_6(x*pi)')
subplot(2,1,2)
plot(x,ys)
title('sinc(6*x/2) / sinc(x/2)')

视图效果

3、高斯调制正弦射频脉冲gauspuls()

gauspuls()函数简介

在 MATLAB 中，可以使用gauspuls()函数来生成高斯调制正弦射频脉冲。该函数可以用于生成具有高斯调制的正弦射频脉冲信号，常用于无线通信系统、雷达系统等领域中的信号模拟和仿真。

gauspuls()函数的语法如下：

y = gauspuls(t, fc, bw, bwr, pwr)

其中：

t：时间序列，表示要生成信号的时间范围；
fc：中心频率，指定高斯调制正弦波的中心频率；
bw：带宽，指定高斯脉冲的3 dB 带宽；
bwr：带宽-中心频率比，用于控制高斯脉冲的形状；
pwr：脉冲功率。

这些参数可以根据需求进行调整，以生成符合特定要求的高斯调制正弦射频脉冲信号。

以下是一个示例，演示如何使用gauspuls()函数生成高斯调制正弦射频脉冲信号：

t = -10e-6:1e-9:10e-6; % 定义时间序列 
fc = 1e9; % 中心频率为1 GHz 
bw = 20e6; % 带宽为20 MHz 
bwr = 0.5; % 带宽-中心频率比为0.5 
pwr = 1; % 脉冲功率为1 
y = gauspuls(t, fc, bw, bwr, pwr); % 生成高斯调制正弦射频脉冲信号 % 绘制高斯调制正弦射频脉冲信号 plot(t, y); 
xlabel('时间（秒）'); 
ylabel('幅度'); 
title('高斯调制正弦射频脉冲信号');

在这个示例中，我们定义了时间序列t、中心频率fc、带宽bw、带宽-中心频率比bwr和脉冲功率pwr，然后使用gauspuls()函数生成了高斯调制正弦射频脉冲信号并绘制了其波形。您可以根据实际需求调整参数，生成不同特性的高斯调制正弦射频脉冲信号。

语法

语法1：yi = gauspuls(t,fc,bw,bwr) 返回一个单位振幅的同相高斯射频脉冲，其分数带宽为bw，相对于归一化信号峰值在bwr dB水平上测量。
语法2：[yi,yq,ye]= gauspuls() 返回射频信号包络。

语法3：tc = gauspuls('cutoff',fc,bw,bwr,tpe) 返回尾随脉冲包络相对于峰值包络幅值降至dB类型以下的截止时间tc。

参数

t:时间

fc:中心频率

bw:部分带宽

bwr:分数带宽参考电平

yi:同相高斯脉冲 yq:正交高斯脉冲

ye:射频信号包络

ct:截止时间

tpe:拖尾脉冲包络电平产生高斯射频脉冲

代码

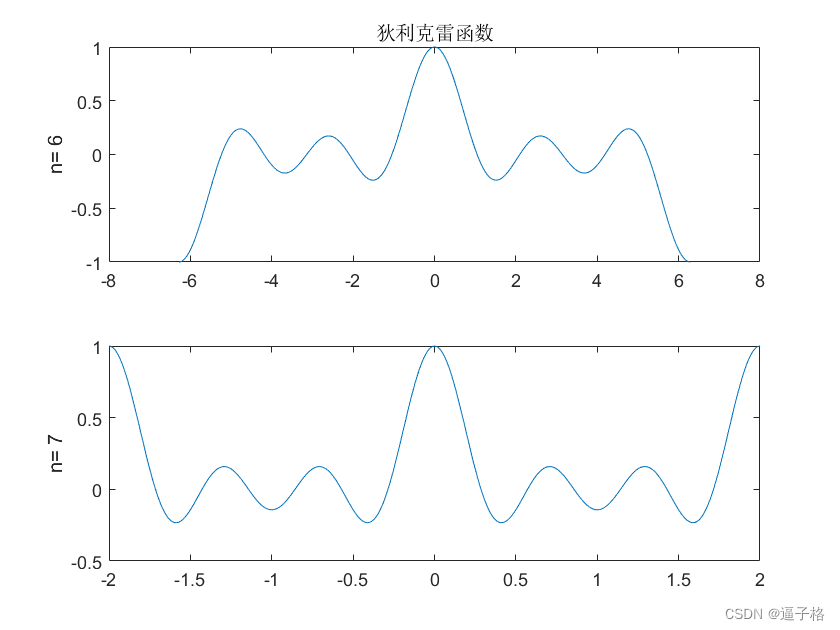
tc = gauspuls('cutoff',50e3,0.6,[],-40); 
t = -tc : 1e-7 : tc; 
[yi,yq,ye] = gauspuls(t,50e3,0.6); 
plot(t,yi,t,yq,t,ye)
legend('同相高斯脉冲','正交高斯脉冲','射频信号包络')

视图效果

4、高斯脉冲gmonopuls()

gmonopuls()函数简介

在 MATLAB 中，可以使用 gmonopuls() 函数来生成单个周期的高斯脉冲信号。这种类型的脉冲在通信系统和雷达系统中经常被使用。

gmonopuls() 函数的语法如下：

y = gmonopuls(t, fc, bwr)

其中：

t：时间序列，表示要生成信号的时间范围；
fc：中心频率，指定高斯脉冲的中心频率；
bwr：带宽-中心频率比，用于控制高斯脉冲的形状。

下面是一个示例，演示如何使用 gmonopuls() 函数生成高斯脉冲信号：

t = -10e-6:1e-9:10e-6; % 定义时间序列 
fc = 1e9; % 中心频率为1 GHz 
bwr = 0.5; % 带宽-中心频率比为0.5 
y = gmonopuls(t,fc,bwr); % 生成高斯脉冲信号 % 绘制高斯脉冲信号 
plot(t, y); 
xlabel('时间（秒）'); 
ylabel('幅度'); 
title('高斯脉冲信号');

在这个示例中，我们定义了时间序列 t 、中心频率 fc 和带宽-中心频率比 bwr ，然后使用 gmonopuls() 函数生成了高斯脉冲信号并绘制了其波形。您可以根据实际需求调整参数，生成不同特性的高斯脉冲信号。

语法

语法1：y = gmonopuls(t,fc) 返回中心频率为fc的单位振幅高斯单脉冲在阵列t中指示的时间点的样本。
语法2：tc = gmonopuls('cutoff',fc) 返回脉冲的最大振幅和最小振幅之间的持续时间。

参数

t:时间 fc:中心频率 y:单脉冲 tc:时间差

1）高斯单脉冲

代码

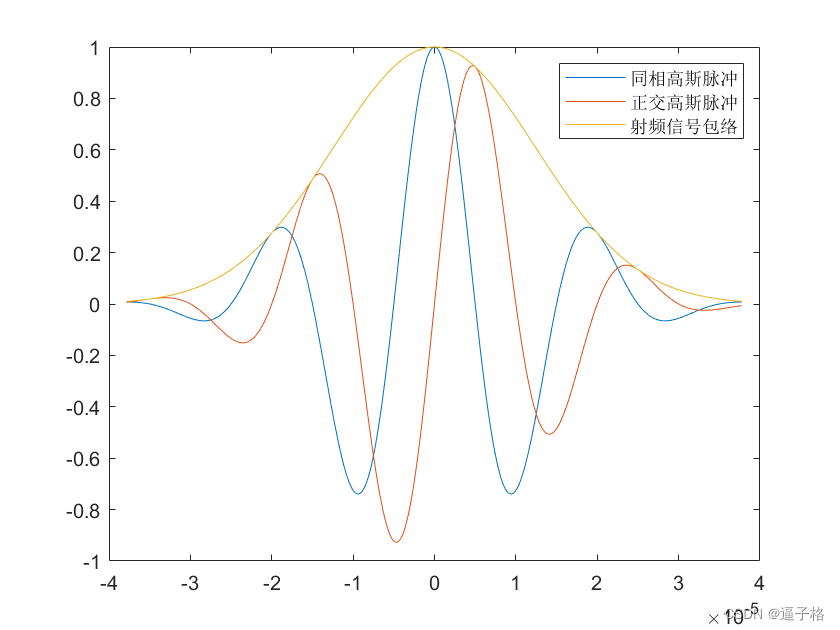
fc = 1e9;
fs = 150e9;
tc = gmonopuls('cutoff',fc);
t  = -2*tc:1/fs:2*tc;
y = gmonopuls(t,fc);
sg = 1/(2*pi*fc);
ys = exp(1/2)*t/sg.*exp(-(t/sg).^2/2);%单脉冲方程
plot(t,y,t,ys,'p')
legend('高斯单脉冲','单脉冲方程')

视图效果

2）高斯脉冲序列

代码

fc = 1e9;
fs = 150e9;
tc = gmonopuls('cutoff',fc);
t  = -2*tc:1/fs:2*tc;
y = gmonopuls(t,fc);
sg = 1/(2*pi*fc);
ys = exp(1/2)*t/sg.*exp(-(t/sg).^2/2);%单脉冲方程
plot(t,y,t,ys,'p')
%高斯单脉冲脉冲序列
fc = 1e9;
fs = 150e9;
tc = gmonopuls('cutoff',fc);
c = ((-5:5)*7.5+2.5)*1e-9;%采样间隔
t  = -150*tc:1/fs:150*tc;%时间轴设置
gp = pulstran(t,c,'gmonopuls',fc);%脉冲序列
plot(t,gp)
legend('高斯单脉冲序列')