Matlab源代码位于: Aquila Optimizer: A meta-heuristic optimization
algorithm - File Exchange - MATLAB Central
(mathworks.cn)
1 Aquila优化算法
AO是一种基于种群优化方法,受启发于Aquila捕获猎物的方式。Aquila捕获猎物的方式主要有四种:(1)有垂直弯曲的高空翱翔(2)用短滑翔攻击的轮廓飞行(3)带缓慢下降的低空飞行(4)走和抓取猎物
对以上四种方法进行建模:
1.1 解决方案的初始化
在给定问题的上界(UB)和下界(LB)使用公式2
随机生成候选集(X,如公式1所示),获得的最优解被认为是在每次迭代过程中的近似优化解。
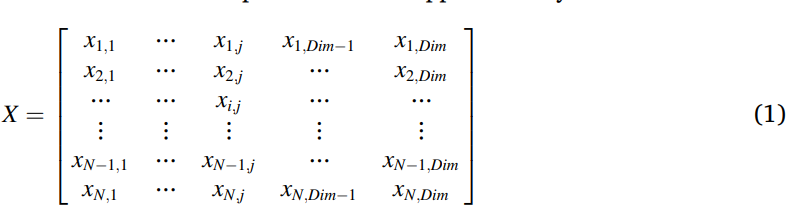
在公式2中,候选集(Xij)=随机数(rand)*(给定问题的第j个上界(UBj)-给定问题的第j个下界(LBj))+给定问题的第j个下界(LBj) ,N表示候选集的总数量,Dim表示问题维度的大小。
1.2 AO的数学模型
1.2.1 扩展探索(X1)
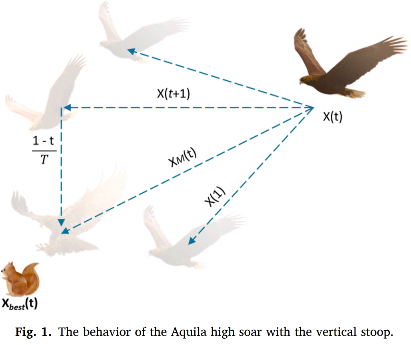
扩展搜索的行为示意图如图1所示。被建模为公式3:
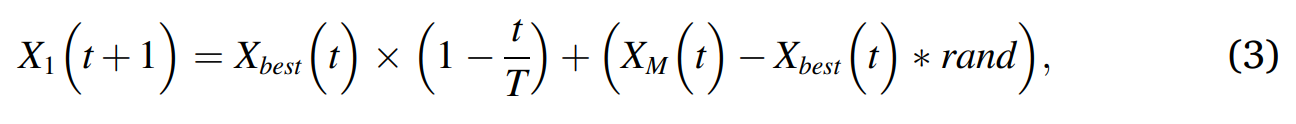
在公式3中,第t次迭代的下一次迭代解(X1(t+1)) = 总共的第t次迭代中最好的解(Xbest(t)) × 通过迭代次数去控制探索范围的等式(1-t/T) + 第t次迭代中所有解的均值(Xm(t))(如公式4所示)- 总共的第t次迭代中最好的解(Xbest(t)) × 位于0和1的随机值(rand) ,t代表现在的迭代次数,T代表总共的迭代次数。
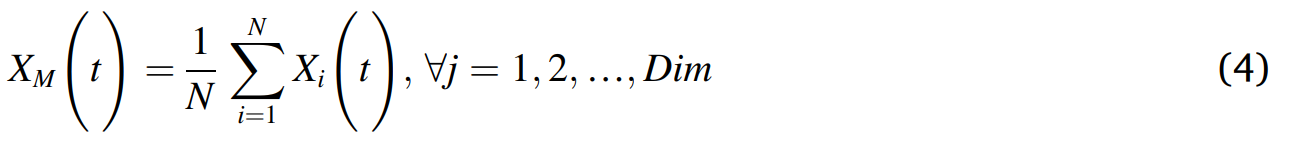
1.2.2 缩小探索范围(X2)
缩小探索范围的行为示意图如图2所示。被建模为公式5:

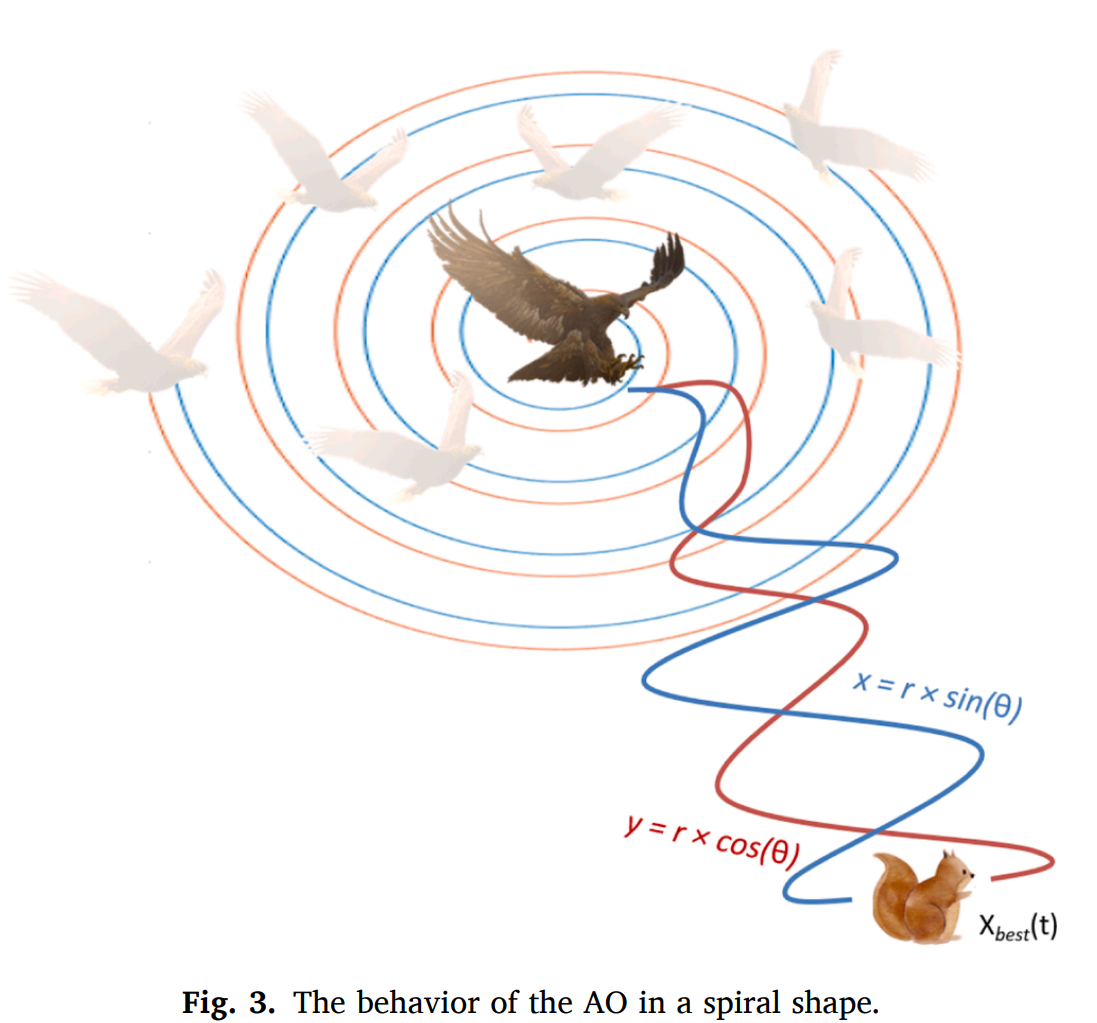
在公式5中,第t次迭代的下一次迭代解(X2(t+1)) = 总共的第t次迭代中最好的解 (Xbest(t)) × 征费飞行分布函数(Levy(D))(如公式6所示)+ 第i次迭代时在[1 N]范围内取的随机解(XR(t))+(搜索中的螺旋形(y)-搜索中的螺旋形(x))×位于0和1的随机值(rand),x和y如公式8、9所示,图3展示了螺旋计算的示意图:

在公式6中,征费飞行分布函数(Levy(D)) = 固定值0.01(s) ×(位于0和1之间的随机数(rand)× σ (如公式7所示))/ | 位于0和1之间的随机数(v)|的1/β次方,其中β是固定值1.5。
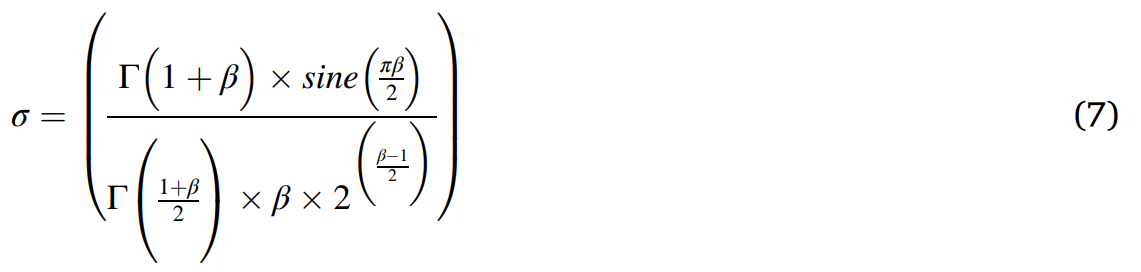

其中

在公式10中,r = 位于1至20的固定搜索周期(r1)+ 0.00565(U) × 从1到搜索空间的长度(Dim) 的整数(D1),在公式11中, ω代表0.05。

1.2.3 扩展开发(X3)
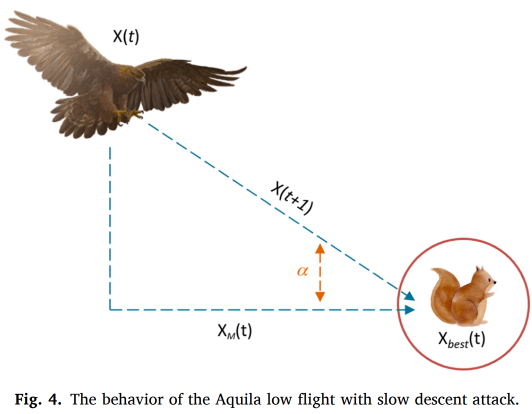
扩展开发的行为示意图如图4所示。被建模为公式13:
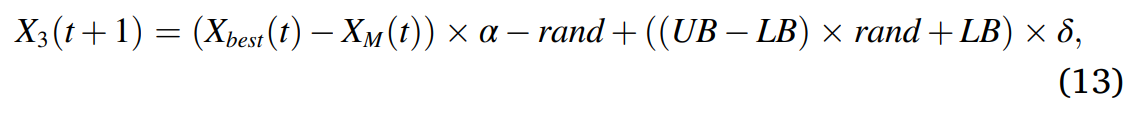
在公式13中,第t次迭代的下一次迭代解 (X3(t+1)) =(总共的第t次迭代中最好的解 (Xbest(t)) - 第t次迭代中所有解的均值(Xm(t)))× 较小的开采调整参数0.01(ɑ) - 位于0到1的随机数(rand) +((给定问题的上界(UB) -给定问题的下界(LB))× 位于0到1的随机数(rand) + 给定问题的下界(LB)) × 较小的开采调整参数0.01(ʠ)。
1.2.4 缩小开发范围(X4)
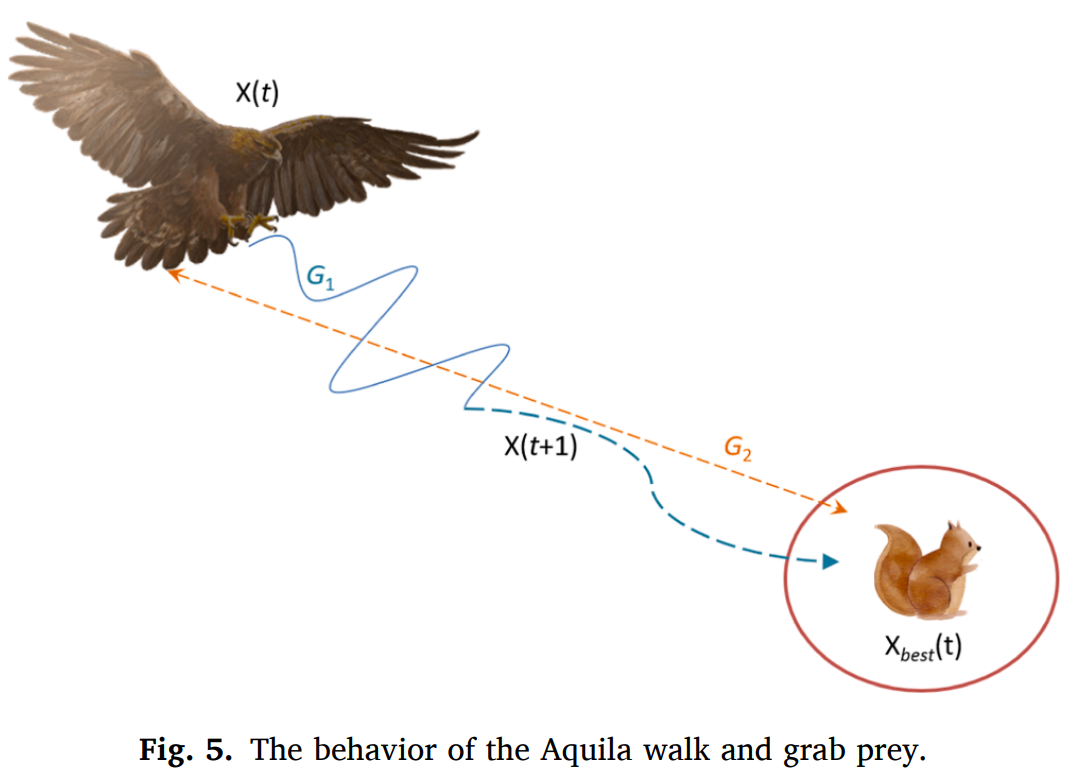
缩小开发范围的行为示意图如图5所示。被建模为公式14:
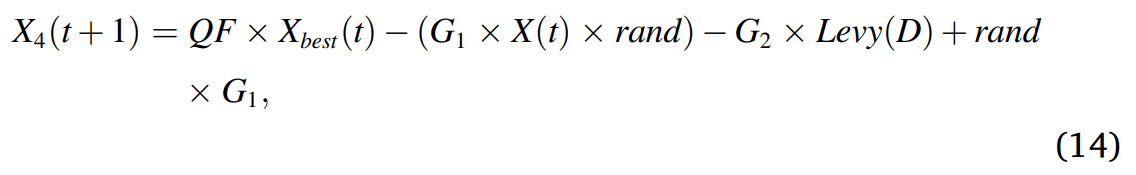
在公式14中, 第t次迭代的下一次迭代解 (X4(t+1)) = 用于平衡搜索策略的质量函数(QF)(如公式15所示)× 总共的第t次迭代中最好的解 (Xbest(t)) - 在奔跑过程中用来追踪猎物的各种AO运动(G1)(如公式16所示)× 第t次迭代解(X(t)) × 0到1的随机数(rand) - 表示AO在从第一个位置(1)到最后一个位置(t)的私奔过程中用于跟踪猎物的飞行斜率(G2)(如公式17所示)× 征费飞行分布函数(Levy(D))(如公式6所示)+ 0到1的随机数(rand) × 在奔跑过程中用来追踪猎物的各种AO运动(G1)(如公式16所示):

2 matlab代码(部分)
% AO函数
% input:N群体数目,T迭代次数,LB问题最低下限,UB问题最高下限,Dim问题维度,F_obj目标函数的句柄,用于评估解的质量
% output:Best_FF AO算法获得的最佳解,Best_P AO算法找到目标函数的最优值
function [Best_FF,Best_P,conv]=AO(N,T,LB,UB,Dim,F_obj)
Best_P=zeros(1,Dim);
Best_FF=inf; % inf无穷大,全局最优解% 解决方案的初始化
X=initialization(N,Dim,UB,LB);
Xnew=X;
Ffun=zeros(1,size(X,1)); % 1*N,存储每个解的目标函数值(最优)
Ffun_new=zeros(1,size(Xnew,1)); % 1*N,存储每个解的目标函数值(当前)t=1;alpha=0.1;
delta=0.1;while t<T+1% 循环处理每个解for i=1:size(X,1)% 判断是否超过上界或者下界F_UB=X(i,:)>UB;F_LB=X(i,:)<LB;% 修正超过边界的解,超过上界的设为UB,超过下界的设为LBX(i,:)=(X(i,:).*(~(F_UB+F_LB)))+UB.*F_UB+LB.*F_LB;% 计算修正解的目标函数值,用于评估解的质量Ffun(1,i)=F_obj(X(i,:));% 更新最优解和最优目标函数值if Ffun(1,i)<Best_FFBest_FF=Ffun(1,i);Best_P=X(i,:);endendG2=2*rand()-1; % Eq. (16)在奔跑过程中用来追踪猎物的各种AO运动G1=2*(1-(t/T)); % Eq. (17)表示AO在从第一个位置(1)到最后一个位置(t)的私奔过程中用于跟踪猎物的飞行斜率(G2)to = 1:Dim;u = .0265;r0 = 10;r = r0 +u*to; % Eq. (10)omega = .005; phi0 = 3*pi/2;phi = -omega*to+phi0; % Eq. (11)x = r .* sin(phi); % Eq. (9)y = r .* cos(phi); % Eq. (10)QF=t^((2*rand()-1)/(1-T)^2); % Eq. (15)% AO begin-------------------------------------------------------------------------------------for i=1:size(X,1)% 扩展探索(X1) -------------------------------------------------------------------------------------if t<=(2/3)*Tif rand <0.5Xnew(i,:)=Best_P(1,:)*(1-t/T)+(mean(X(i,:))-Best_P(1,:))*rand(); % Eq. (3) and Eq. (4)Ffun_new(1,i)=F_obj(Xnew(i,:));if Ffun_new(1,i)<Ffun(1,i)X(i,:)=Xnew(i,:);Ffun(1,i)=Ffun_new(1,i);endelse% 缩小探索范围(X2) -------------------------------------------------------------------------------------Xnew(i,:)=Best_P(1,:).*Levy(Dim)+X((floor(N*rand()+1)),:)+(y-x)*rand; % Eq. (5)Ffun_new(1,i)=F_obj(Xnew(i,:));if Ffun_new(1,i)<Ffun(1,i)X(i,:)=Xnew(i,:);Ffun(1,i)=Ffun_new(1,i);endend% 扩展开发(X3) -------------------------------------------------------------------------------------elseif rand<0.5Xnew(i,:)=(Best_P(1,:)-mean(X))*alpha-rand+((UB-LB)*rand+LB)*delta; % Eq. (13)Ffun_new(1,i)=F_obj(Xnew(i,:));if Ffun_new(1,i)<Ffun(1,i)X(i,:)=Xnew(i,:);Ffun(1,i)=Ffun_new(1,i);endelse% 缩小开发范围(X4) -------------------------------------------------------------------------------------Xnew(i,:)=QF*Best_P(1,:)-(G2*X(i,:)*rand)-G1.*Levy(Dim)+rand*G2; % Eq. (14)Ffun_new(1,i)=F_obj(Xnew(i,:));if Ffun_new(1,i)<Ffun(1,i)X(i,:)=Xnew(i,:);Ffun(1,i)=Ffun_new(1,i);endendendend% AO end-------------------------------------------------------------------------------------% 判断是否达到迭代次数100,如果达到则展示结果if mod(t,100)==0display(['At iteration ', num2str(t), ' the best solution fitness is ', num2str(Best_FF)]);endconv(t)=Best_FF; % 每一轮迭代的最优值t=t+1;
endendfunction o=Levy(d)
beta=1.5;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);
o=step;
end
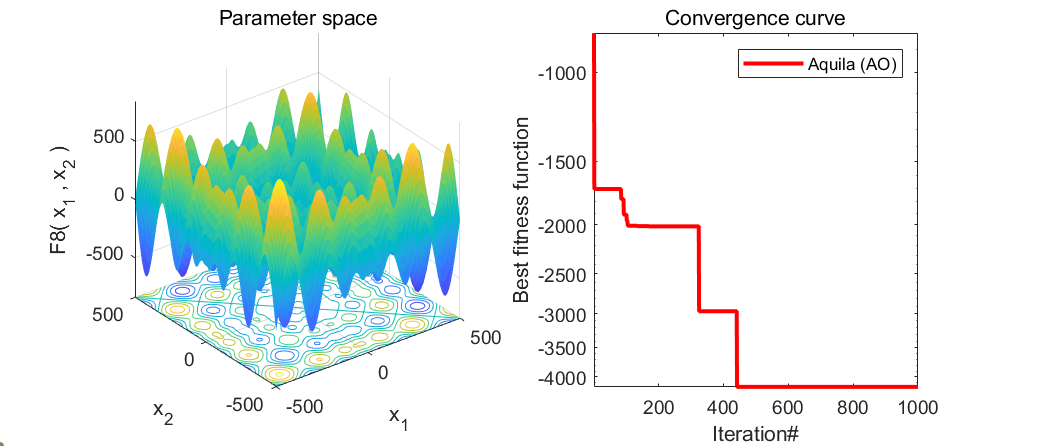
运行结果:
参考: https://doi.org/10.1016/j.cie.2021.107250