问题描述

有13个外表一模一样的小球产品，其中有一个是次品，其质量与其他12个略有差别，但不知道是重还是轻。这13个球上都有标号，现在给你-架天平，只能使用三次，把这个次品小球找出来。注:必须要考虑到所有的可能。

解决方案

思来想去，选择了百度，参考https://blog.sciencenet.cn/blog-582408-658699.html 袁乾前辈的解决方案。

假设分为：A1，A2，A3，A4，B1，B2，B3，B4，C1，C2，C3，C4，C5三组。
第一称，称A和B组
结果：平衡，次品在C中，可以找出。（以A1，A2,A3和C1,C2,C3进行比较，1）如平衡，则A1比C4，平衡，则为C5,否则为C4。2）如不平衡，则问题在C1,C2,C3中，假设C1，C2，C3要重一些(假设是合理的)，比C1,C2，如平衡,次品为C3，否则，如不平衡，可推断出结果，则重的一方是次品。）
不平衡，不失一般性，假设A这边要重一些，现在知道的信息有，C中时标准的，A这边要沉一些，如果次品轻一些，那么次品在B里面，如果次品重一些，那么次品在A里面。据此，开始下一步。
第二称：取C组，和A1,A2,A3,B1,B2.
结果：平衡，因为C中都是正常的，则问题出现在A4，B1，B2当中。
第三称：取C1,C2和A4,B3. 结果：平衡，次品是B4(找出)。如不平衡，如果C这边沉一些，则说明次品轻一些，则结合第一次称的结果，可知，次品在B小组里面，则次品为B1(找出)，如C这边要轻一些，则说明次品要重一些，则次品是A4.
现在讨论第二称不平衡的情况：第二称不平衡，则说明问题在A1，A2，A3，B1，B2里面，根据现有结果，如果C这边沉一些，则可知次品轻一些，结合第一称的结果，则问题出现在B1,B2里面，则第三称对比B1，B2就知道了(找出)。如果C这边要轻一些，说明次品要重一些，结合第一称的结果，问题出现在A1，A2,A3当中，第三称对于A1,A2，如果平衡，则是A3，如果不平衡，则是A1，A2中重的一方。

袁前辈的图和文字描述存在部分误写，博主这里已做略微订正。
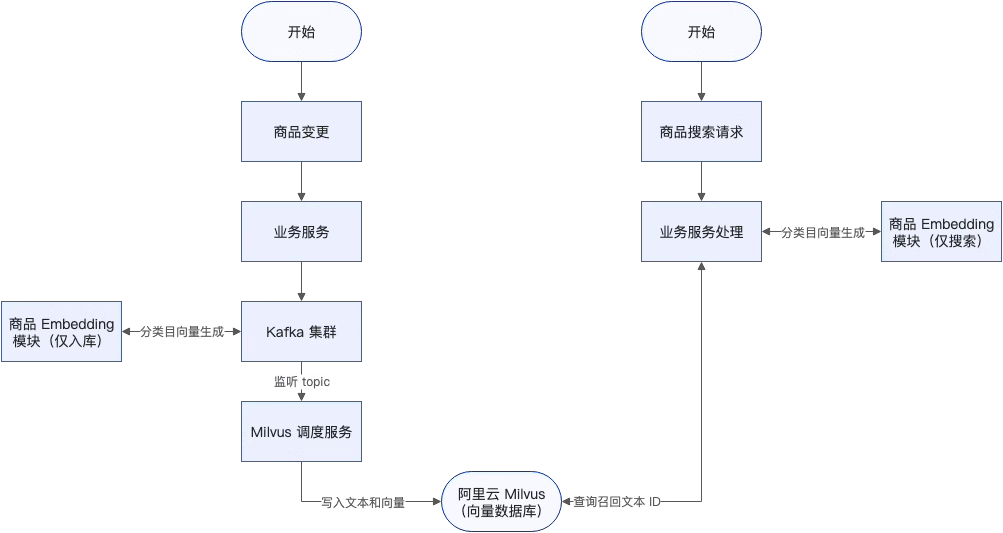
重绘称量流程图如下：

PS:右侧的三个方案困扰我许久，终于得到解答，拜谢前辈的无私分享。