669修剪二叉树 

力扣题目链接

题目描述：

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

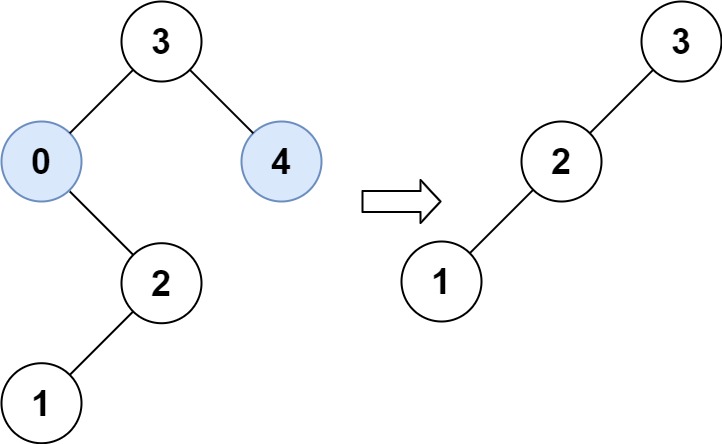
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

代码：

 class Solution {  
public:  TreeNode* trimBST(TreeNode* root, int low, int high) {  if (root == nullptr) return nullptr;  if (root->val < low) {  return trimBST(root->right, low, high);  }  if (root->val > high) {  return trimBST(root->left, low, high);  }  root->left = trimBST(root->left, low, high);  root->right = trimBST(root->right, low, high);  return root;  }  
};  

代码解释：
 

详细解释

1. Base Case:

   • 如果当前节点是空 (nullptr)，直接返回空，因为没有树需要修剪。

2. 修剪逻辑:

   • 节点值小于 low：
     如果当前节点值 root->val < low，这意味着当前节点和它的左子树所有节点都小于 low，需要被修剪掉。所以，我们修剪右子树。

     if (root->val < low) { TreeNode* rightTrimmed = trimBST(root->right, low, high); return rightTrimmed; }

     这里，对右子树调用 trimBST 递归函数，并将修剪后的右子树赋值给 rightTrimmed，然后释放当前节点，返回修剪后的右子树。

   • 节点值大于 high：
     如果当前节点值 root->val > high，这意味着当前节点和它的右子树所有节点都大于 high，需要被修剪掉。所以，我们修剪左子树。

     if (root->val > high) { TreeNode* leftTrimmed = trimBST(root->left, low, high); return leftTrimmed; }

     这里，对左子树调用 trimBST 函数，并将修剪后的左子树赋值给 leftTrimmed，然后释放当前节点，返回修剪后的左子树。

   • 节点值在区间 [low, high] 之间：
     如果当前节点的值在 [low, high] 之间，那么当前节点是需要保留的节点。但是仍然需要继续修剪其左右子树。

     root->left = trimBST(root->left, low, high); root->right = trimBST(root->right, low, high); return root;

     这里，通过递归处理左右子树，并将返回的修剪后的子树赋值给当前节点的左右子节点，最后返回当前节点。

108将有序数组转变为平衡搜索二叉树

力扣题目链接

题目描述：

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 

平衡

 二叉搜索树。

示例 1：

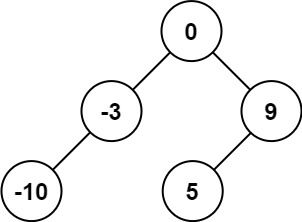
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

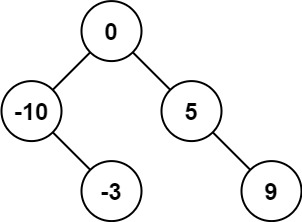
示例 2：

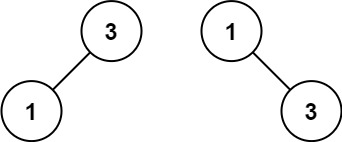
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

代码：

#include <vector>  // 树节点的定义  
struct TreeNode {  int val;               // 节点的值  TreeNode *left;        // 左子节点  TreeNode *right;       // 右子节点  TreeNode() : val(0), left(nullptr), right(nullptr) {}     // 无参构造函数  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} // 有参构造函数  TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} // 完整构造函数  
};  class Solution {  
public:  // 递归构造 BST 的辅助函数  TreeNode* travesal(std::vector<int>& nums, int left, int right) {  // 基准条件：如果左索引超过右索引，返回空指针  if(left > right) return nullptr;  // 计算中间索引，避免整数溢出的安全写法  int mid = left + (right - left) / 2;  // 创建根节点，值为数组中间位置的值  TreeNode* root = new TreeNode(nums[mid]);  // 递归构造左子树，范围为[left, mid-1]  root->left = travesal(nums, left, mid - 1);  // 递归构造右子树，范围为[mid + 1, right]  root->right = travesal(nums, mid + 1, right);  // 返回根节点  return root;  }  // 主函数，将有序数组转换为 BST  TreeNode* sortedArrayToBST(std::vector<int>& nums) {  // 初始调用辅助函数，范围为整个数组  int left = 0;  int right = nums.size() - 1;  // 获取并返回构造出的 BST 的根节点  TreeNode* root = travesal(nums, left, right);  return root;  }  
};  

详细解释

1. TreeNode 结构体
   定义了树节点，其中 val 是节点的值，left 和 right 分别是左子节点和右子节点。无参构造函数将节点默认初始化为值 0 和空子节点，有参构造函数将节点的值初始化为给定值，最后一个构造函数同时初始化节点的值和子节点。

2. travesal 函数（递归辅助函数）
   这个函数递归地构建 BST：

   • 基准条件：当 left 超过 right 时，返回空指针，表示该子树为空。
   • 中间索引：计算中间索引 mid，它是子数组的中间元素的位置。
   • 创建根节点：使用中间元素创建根节点。
   • 分别递归构建左子树和右子树：递归调用 travesal 函数，分别构建左子树（范围为 left 到 mid-1）和右子树（范围为 mid+1 到 right）。
   • 返回根节点：返回该子树的根节点。

3. sortedArrayToBST 函数（主函数）
   这是主函数，调用递归辅助函数来构建 BST：

   • 初始化 left 和 right 索引，分别为数组的起始和结束位置。
   • 调用 travesal 函数来构建 BST，并得到根节点。
   • 返回最终构建好的根节点。

举个例子:

假设输入的有序数组是 [1, 2, 3, 4, 5, 6, 7]，我们将通过该方法将其转换为高度平衡的 BST。

1. 取数组的中间元素 4 作为根节点。
2. 将左半部分 [1, 2, 3] 递归构建左子树：
   • 子数组 [1, 2, 3] 的中间元素 2 作为左子树的根节点。
   • 子数组 [1] 递归构建左子树：1 作为左子树的根节点。
   • 子数组 [3] 递归构建右子树：3 作为右子树的根节点。
3. 将右半部分 [5, 6, 7] 递归构建右子树：
   • 子数组 [5, 6, 7] 的中间元素 6 作为右子树的根节点。
   • 子数组 [5] 递归构建左子树：5 作为左子树的根节点。
   • 子数组 [7] 递归构建右子树：7 作为右子树的根节点。

 

538把搜索二叉树变为累加二叉树

力扣题目链接

题目描述：

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

注意：本题和 1038: . - 力扣（LeetCode） 相同

示例 1：

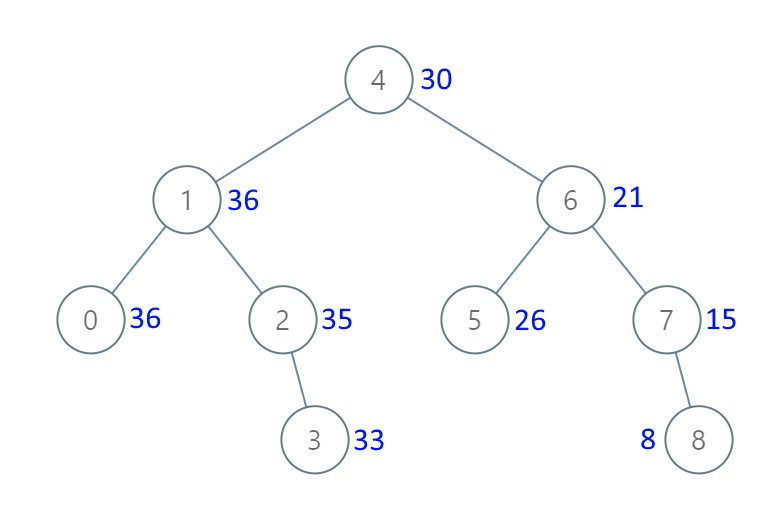
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

代码：

class Solution {
public:int pre=0;TreeNode* convert(TreeNode* cur){if(cur==NULL)return NULL;convert(cur->right);cur->val+=pre;pre=cur->val;convert(cur->left);return cur;}TreeNode* convertBST(TreeNode* root) {return convert(root);}
};

这题需要注意的是遍历顺序，逆中序遍历，其他的没什么很简单