算法日记day 20（中序后序遍历序列构造二叉树|最大、合并、搜索二叉树）

一、中序后序序列构造二叉树

题目：

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

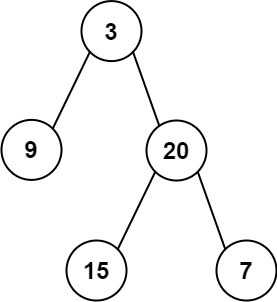
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

思路：

中序遍历顺序：左、中、右后序遍历顺序：左、右、中

首先在后序中确定最后一个节点为二叉树的根节点，再以此根节点在中序遍历中寻找左子树和右子树，和后序遍历中的左子树和右子树，依次循环递归其左右子树，直到遍历完所有节点为止

代码：

public class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {// 检查特殊情况，如果输入的中序或后序序列长度为0，则返回空树if (postorder.length == 0 || inorder.length == 0) {return null;}// 调用递归辅助方法来构建二叉树，并返回根节点return buildHelper(inorder, 0, inorder.length, postorder, 0, postorder.length);}private TreeNode buildHelper(int[] inorder, int inorderStart, int inorderEnd,int[] postorder, int postorderStart, int postorderEnd) {// 如果后序序列的起始索引等于结束索引，说明当前子树为空，返回nullif (postorderStart == postorderEnd) {return null;}// 后序遍历序列的最后一个元素是当前子树的根节点值int rootVal = postorder[postorderEnd - 1];TreeNode root = new TreeNode(rootVal); // 创建根节点int middleIndex;// 在中序遍历序列中找到根节点的位置for (middleIndex = inorderStart; middleIndex < inorderEnd; middleIndex++) {if (inorder[middleIndex] == rootVal) {break;}}// 计算左子树和右子树在中序遍历序列中的边界int leftInorderStart = inorderStart;int leftInorderEnd = middleIndex;int rightInorderStart = middleIndex + 1;int rightInorderEnd = inorderEnd;// 计算左子树和右子树在后序遍历序列中的边界int leftPostorderStart = postorderStart;int leftPostorderEnd = postorderStart + (middleIndex - inorderStart);int rightPostorderStart = leftPostorderEnd;int rightPostorderEnd = postorderEnd - 1;// 递归构建左子树和右子树，并连接到当前根节点root.left = buildHelper(inorder, leftInorderStart, leftInorderEnd,postorder, leftPostorderStart, leftPostorderEnd);root.right = buildHelper(inorder, rightInorderStart, rightInorderEnd,postorder, rightPostorderStart, rightPostorderEnd);return root; // 返回当前根节点}
}

buildTree 方法接收两个参数：inorder 表示中序遍历序列，postorder 表示后序遍历序列。
首先检查特殊情况：如果 postorder 或 inorder 的长度为 0，则返回 null，表示空树。
调用 buildHelper 方法来实际构建二叉树，并返回根节点。
buildHelper 方法是一个递归方法，用来构建二叉树的具体逻辑。
首先检查递归终止条件：如果 postorderStart == postorderEnd，说明当前子序列为空，返回 null。
从 postorder 中获取当前子树的根节点值 rootVal，并创建根节点 root。
在 inorder 中查找根节点值 rootVal 的位置 middleIndex，用于分割左右子树的中序遍历序列。
计算左子树和右子树的中序遍历序列的起始和结束索引。
根据中序遍历序列的划分，计算左右子树在后序遍历序列中的起始和结束索引。
递归构建左子树和右子树，将其分别连接到当前根节点 root 的左右孩子上。

二、最大二叉树

题目：

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

示例 1：

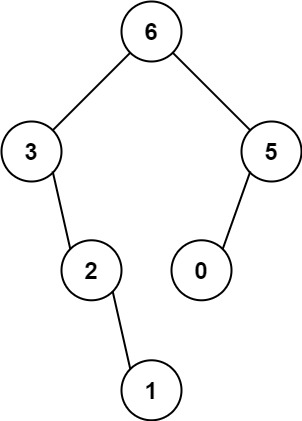
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。- 空数组，无子节点。- [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。- 空数组，无子节点。- 只有一个元素，所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。- 只有一个元素，所以子节点是一个值为 0 的节点。- 空数组，无子节点。

示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

思路：

首先遍历数组中的最大值为根节点，后以该根节点为分割点区分开左右子树，然后分别对左右子树中的元素再进行如上操作，找到每次分割的左右子树中的最大元素作为下一层的父节点

代码：

public TreeNode constructMax(int[] nums, int leftIndex, int rightIndex) {if (rightIndex - leftIndex < 1)return null;if (rightIndex - leftIndex == 1)return new TreeNode(nums[leftIndex]);int maxIndex = leftIndex;    int maxValue = nums[maxIndex];// 寻找最大值及其索引for (int i = leftIndex + 1; i < rightIndex; i++) {if (nums[i] > maxValue) {maxValue = nums[i];maxIndex = i;}}// 用最大值构建根节点TreeNode root = new TreeNode(maxValue);// 递归构建左子树和右子树root.left = constructMax(nums, leftIndex, maxIndex);root.right = constructMax(nums, maxIndex + 1, rightIndex);return root;
}

constructMax 方法接受四个参数：nums 数组、左边界 leftIndex 和右边界 rightIndex。
首先，检查当前子数组的长度，如果小于等于 1，则返回相应的树结点（空结点或叶子结点）。
否则，通过遍历找到当前子数组中的最大值及其索引 maxIndex。
创建根节点 root，值为 maxValue。
递归地构建左子树和右子树：
- 左子树递归调用 constructMax(nums, leftIndex, maxIndex)，处理左半部分的数组。
- 右子树递归调用 constructMax(nums, maxIndex + 1, rightIndex)，处理右半部分的数组。

public TreeNode constructMaximumBinaryTree(int[] nums) {return constructMax(nums, 0, nums.length);
}

返回constructMax 方法构建的子树的根节点 root，最终完成整棵最大二叉树的构建。

三、合并二叉树

题目：

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

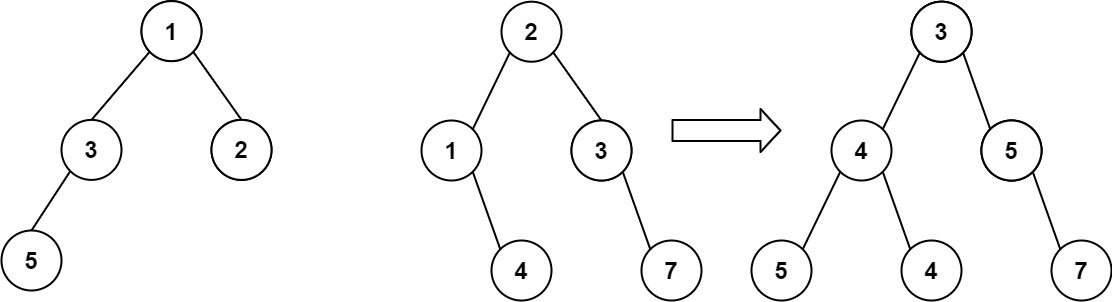
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

思路：

同时操作两个二叉树对应的节点进行相加操作，可以分情况讨论，两树间存在空节点、两树间都有节点的情况

第一类代码：

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {// 如果两棵树的当前节点都为空，则返回空节点if (root1 == null && root2 == null) {return null;}// 创建新的树节点，值先设为0TreeNode root = new TreeNode(0);// 如果root1为空但root2不为空，以root2的值作为当前节点的值，递归处理左右子树if (root1 == null && root2 != null) {root.val = root2.val;root.left = mergeTrees(null, root2.left);root.right = mergeTrees(null, root2.right);} // 如果root1不为空但root2为空，以root1的值作为当前节点的值，递归处理左右子树else if (root1 != null && root2 == null) {root.val = root1.val;root.left = mergeTrees(root1.left, null);root.right = mergeTrees(root1.right, null);} // 如果root1和root2都不为空，以它们的值相加作为当前节点的值，递归处理左右子树else {root.val = root1.val + root2.val;root.left = mergeTrees(root1.left, root2.left);root.right = mergeTrees(root1.right, root2.right);}// 返回合并后的根节点return root;
}

使用递归的简洁方法

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {// 如果root1为空，则返回root2if (root1 == null)return root2;// 如果root2为空，则返回root1if (root2 == null)return root1;// 如果root1和root2都不为空，将它们的值相加root1.val += root2.val;// 递归处理左子树，将合并后的左子树设为root1的左子树root1.left = mergeTrees(root1.left, root2.left);// 递归处理右子树，将合并后的右子树设为root1的右子树root1.right = mergeTrees(root1.right, root2.right);// 返回合并后的根节点root1return root1;
}

空节点处理：
- 首先判断 root1 是否为空。如果 root1 为空，直接返回 root2。这是因为如果有一棵树为空，直接返回另一棵树即可，不需要再合并操作。
递归合并：
- 如果 root1 不为空且 root2 也不为空，则将 root1 和 root2 的值相加，更新 root1 的值。
- 然后分别递归合并它们的左子树和右子树：
  - root1.left = mergeTrees(root1.left, root2.left);
  - root1.right = mergeTrees(root1.right, root2.right);
- 这样就递归地将 root1 和 root2 的左子树和右子树合并，并将合并后的子树作为 root1 的左右子树。

四、二叉搜索树中的搜索

二叉搜索树：左子树的值比根节点小，右子树的值比根节点大，且其每个子树也都是二叉搜索树

题目：

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:

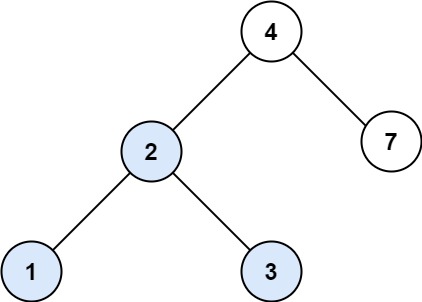
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

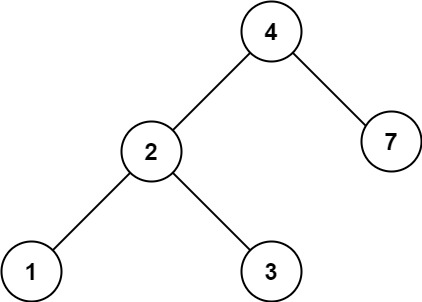
输入：root = [4,2,7,1,3], val = 5
输出：[]

代码：

递归

//递归法
public TreeNode searchBST(TreeNode root, int val) {// 如果当前节点为空，表示已经搜索到叶子节点仍未找到目标值，返回 nullif (root == null)return null;// 如果当前节点的值等于目标值，直接返回当前节点if (root.val == val)return root;// 声明一个用于存放搜索结果的变量，默认为 nullTreeNode result = null;// 如果目标值小于当前节点的值，向左子树递归搜索if (val < root.val) {result = searchBST(root.left, val);}// 如果目标值大于当前节点的值，向右子树递归搜索if (val > root.val) {result = searchBST(root.right, val);}// 返回最终的搜索结果，可能为找到的节点或者 nullreturn result;
}

空节点处理：
- 首先检查当前节点 root 是否为空。如果为空，意味着在当前分支上已经搜索到叶子节点仍未找到目标值，因此返回 null 表示未找到。
目标值匹配：
- 如果当前节点的值 root.val 等于目标值 val，则直接返回当前节点 root，表示找到了目标节点。
递归搜索：
- 如果目标值 val 小于当前节点的值 root.val，则递归调用 searchBST(root.left, val)，在左子树中继续搜索目标值。
- 如果目标值 val 大于当前节点的值 root.val，则递归调用 searchBST(root.right, val)，在右子树中继续搜索目标值。
返回结果：
- 无论是从左子树还是右子树返回的结果，将其赋给 result 变量。
- 最终返回 result，可能是找到的目标节点或者 null（如果未找到）。

迭代

//迭代法
public TreeNode searchBST(TreeNode root, int val) {// 使用循环来在二叉搜索树中搜索目标值while (root != null) {if (val < root.val) {root = root.left;  // 如果目标值小于当前节点的值，向左子树移动} else if (val > root.val) {root = root.right; // 如果目标值大于当前节点的值，向右子树移动} else {return root; // 找到目标节点，返回当前节点}}return null; // 如果循环结束仍未找到目标节点，返回 null
}