java算法day27

• 动态规划初步总结
• 509 斐波那契数
• 杨辉三角
• 打家劫舍
• 完全平方数

---

动态规划初步总结

如果你感觉某个问题有很多重叠子问题，使用动态规划是最有效的。
动态规划的过程就是每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心了。贪心是“直接”从局部选最优的。

看到目前的各种教程，目前能看懂的动态规划思想总结就是：
这三步：
1、穷举法（暴力搜索）
2、记忆化搜索（剪枝）
3、改写成迭代形式。

目前我只能一步步的做题来体会动态规划。

---

509 斐波那契数列

目前就拿着上面总结的思想来做做题。

拿到这个题，我上来就想到了递归解法（这也对应着上面的第一点）。然后快速就交了，过了，但是超越百分之5。足以见得效率非常的低。

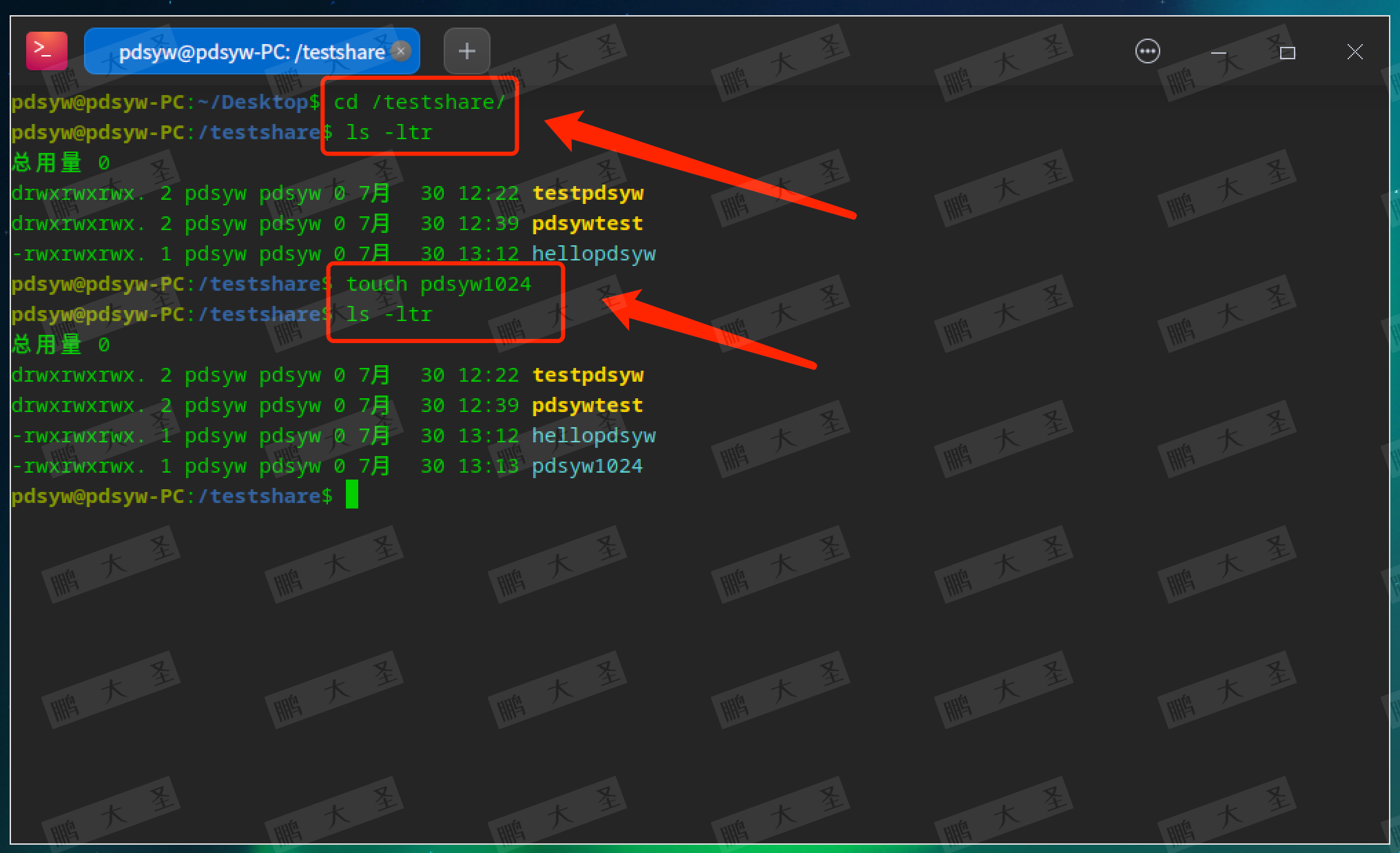
class Solution {public int fib(int n) {if(n == 0){return 0;}if(n == 1){return 1;}return fib(n-2) + fib(n-1);}
}

问题出在哪里，从递归树里就清楚了

从这个计算过程可以看到，存在着大量的重复计算。比如计算f(18)和f(19)的时候，都会计算f(17)，而计算f(17)的过程又需要往下递归，意思说f(17)要算两次。往下那肯定存在更多的重复性计算。所以说这是需要优化的点。

如何优化，如何实现快速访问，这里我们可以想到哈希，下次我要计算之前，我先不着急递归，我先去hash里面看看有没有现成的，直接哪来用。那么按照这样的想法我们就可以创建一个哈希表，至于这个表是什么样的，可以根据题目来。

有时候可能还想不通，那这个hash里面的值是怎么记录下来的，那我只能说要把递归的过程想清楚。
通过上面的代码，算f(5) return f(4) + f(3) 。那么按程序执行顺序来说，肯定是先进f(4)，然后一直往下走
比如f(4) return f(3) + f(2)
f(3) = f(2) + f(1)
然后f(2) = f(1)+f(0) 。可以见得，在不断下去的过程中，f(4),f(3),f(2),f(1),f(0)都会计算。所以说在这最左边的分支，其实就已经把别的分支那些重复的点全计算完了。所以hash就是在这里就完成了计算，怎么算？这个过程中程序要进行计算，hash表直接把这个结果也存到自己的哈希表里不就完事了。

从这个过程，再对上面的递归树做一个优化，你可以看到这样的变化。

是不是感觉2^n级别的复杂度立马变o(n)了。

带备忘录的写法如下：

class Solution {public int fib(int n) {if(n<1){return 0;}int[] memo = new int[31];return helper(n,memo);}int helper(int n,int[] memo){if(n == 1 || n == 2){return 1;}if(memo[n]!=0){return memo[n];}memo[n] = helper(n-1,memo)+helper(n-2,memo);return memo[n];}}

这么这就是dp了吗？还不是！
这其实还是一个自顶向下的解法。

真正的dp是什么。真正的dp是自底向上，从最小的子问题开始，然后逐步构造最大的解，直到达到目标。

动态规划的本质：动态规划的核心是通过解决子问题来解决更大的问题，在斐波那契数的例子中，我们直到每个数都是前两个数的和。

所以这里可以总结出动态规划问题的真正含义了。
我先来说说动态规划是如何解决这个问题的，首先如果清楚子问题是什么样的，然后清楚子问题的初状态，那么我就能够直接从这个子问题出发，不断地进行状态运算，直到状态转移到最终结果。然后这个得到下一个状态的方法，就是所谓的状态转移方程。

所以这里可以总结一个结论：
也就是很多教程里面教的方法：
子问题的识别：
正如你所说，清楚地识别子问题是关键。在斐波那契数列中，子问题就是计算每个 F(i)。

初始状态（基本情况）：
这些是已知的最小子问题的解。在斐波那契数列中，F(0) = 0 和 F(1) = 1。

状态转移：
这是从一个子问题到另一个子问题的过程。在斐波那契数列中，状态转移方程是 F(i) = F(i-1) + F(i-2)。

最终状态：
这是我们最终要求解的问题。在斐波那契数列中，就是计算 F(n)。

从初始状态到最终状态：
正如你所说，我们可以从初始状态开始，通过不断应用状态转移方程，最终达到我们想要的结果。

说的更直白一点：
也就是说，如果我在做题的过程中，搞清楚了什么是子问题，还有初始状态，知道下一个状态该如何正确计算。那么我就能从这个初始状态直接往后推，直到推出最后的正确答案。

---

然后就立马写出了这个题。感觉还是非常清楚的。
子问题怎么找? 这里我看网上一般是通过推广的办法,由f(n)来思考那么是要计算f(n-1)+f(n-2)。那么推广到i就是dp[i] = dp[i-1]+dp[i-2];所以子问题就是计算dp[i-1]和dp[i-2]。往最初的状态倒就是从dp[0] 和 dp[1]开始
状态转移方程是啥？ 就是怎么计算下一个状态，这里状态转移方程就是dp[i] = dp[i-1]+dp[i-2]
最终状态怎么确定？ 就是看dp要到哪停下来。这里就是算dp[n]

dp数组到底怎么初始化？这个我认为一是要根据问题，而是要根据数据的边界。即最大可能取到的状态来确定长度。

class Solution {public int fib(int n) {//快速特判if(n<2){return n;}int[] dp = new int[n+1];dp[0] = 0;dp[1] = 1;for(int i = 2;i<=n;i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
}

提交之后会发现，效率和备忘录那个写法的效率相同
因为这俩的计算纯粹是反过来的关系

然后还可以再进一步优化

是不是发现我们其实只要这个最后的dp[n]，甚至感觉这个dp数组有点多余了。
确实是，我们其实就只需要不断的迭代更新后面两个数字 即 dp[i-1] 和 dp[i-2]
这个技巧就是所谓的状态压缩 空间复杂度直接优化为o1了。
怎么理解状态压缩的应用？就是想想原来的dp数组，有没有一些空间是不必要存储的。

所以这里还有一个究极版本。

class Solution {public int fib(int n) {if(n<2){return n;}int pre = 0;int cur = 1;for(int i = 2;i<=n;i++){//sum是下一个状态int sum = pre+cur;pre = cur;cur = sum;}return cur;}
}

---

零钱兑换

上面的斐波那契还体现不出dp。因为没有求最值问题，现在来看看这个题。
我第一想法就是一个大回溯直接爆搜。果不其然第32个例子直接超时。

接下来就只能看看题解了，用dp来做这个题。

这里得到第一个知识点：能用dp，首先要复合最优子结构，子问题间必须互相独立。
啥叫互相独立，就是子问题之间没有互相影响。
简单来说就是考试，你要拿最高分，比如一共两名，语文和数学。
要拿最高分就是数学考最高，语文考最高。这样就叫独立。
如果你数学考得高了，会导致你语文考不高，那就不叫独立。

所以要自己看看子问题之间有没有互相制约关系，是否相互独立

还有这个看待子问题的角度也非常重要。有时候你子问题找错了，那就可能做不出来了。
对于本题而言，子问题是这样拆分的，比如追求amont = 11（原问题），如果你知道凑出amont = 10的最少硬币数（子问题），那么只需要把子问题的答案（再选一枚面值为1的硬币），就是原问题的答案。还有这怎么看出子问题之间没有互相限制，因为硬币数量是没有限制的。

---

这里又纠正了我看待动态规划问题的思路了。一开始我是没理解倒这个问题中的独立。
1、动态规划的思考方向：
首先，动态理解是要自底向上思考的，而不是从amount=11开始往下想，我从大的开始想，那么我就会老是去想我最后一个面值为1了，那不是有可能对我前面的问题产生影响？
这里主要是方向想错了
2、子问题的定义：
对于金额i，子问题是凑出金额i所需的最少硬币数
3、独立性本质：
当我们说子问题是独立的，我们指的是，求解金额i的最优解，不依赖于如何求解i+1，i+2等更大的金额。（说白了还是方向看错了）。
4、为什么看起来不独立（我之前的思想）：
因为我方向想反了。

现在来模拟这个问题
举例说明：
假设硬币面值为 [1, 2, 5]，我们要凑出 11。

我们首先解决小额问题：1, 2, 3, 4, 5, …
当我们到达 11 时，我们考虑的是：
dp[11] = min(dp[10] + 1, dp[9] + 1, dp[6] + 1)
这里的 dp[10], dp[9], dp[6] 都已经是各自最优的解了
我们不是在考虑 “用1个1硬币然后解决10”，而是在比较 “10的最优解+1” 和其他可能性

独立性的证明：

如果 dp[10] 是最优的（假设是3个硬币），那么无论我们如何解决 11，都不会影响 10 的这个最优解。
即使我们选择了 “dp[9] + 1个2硬币” 作为 11 的最优解，这也不会改变 10 的最优解仍然是 3 个硬币这个事实。