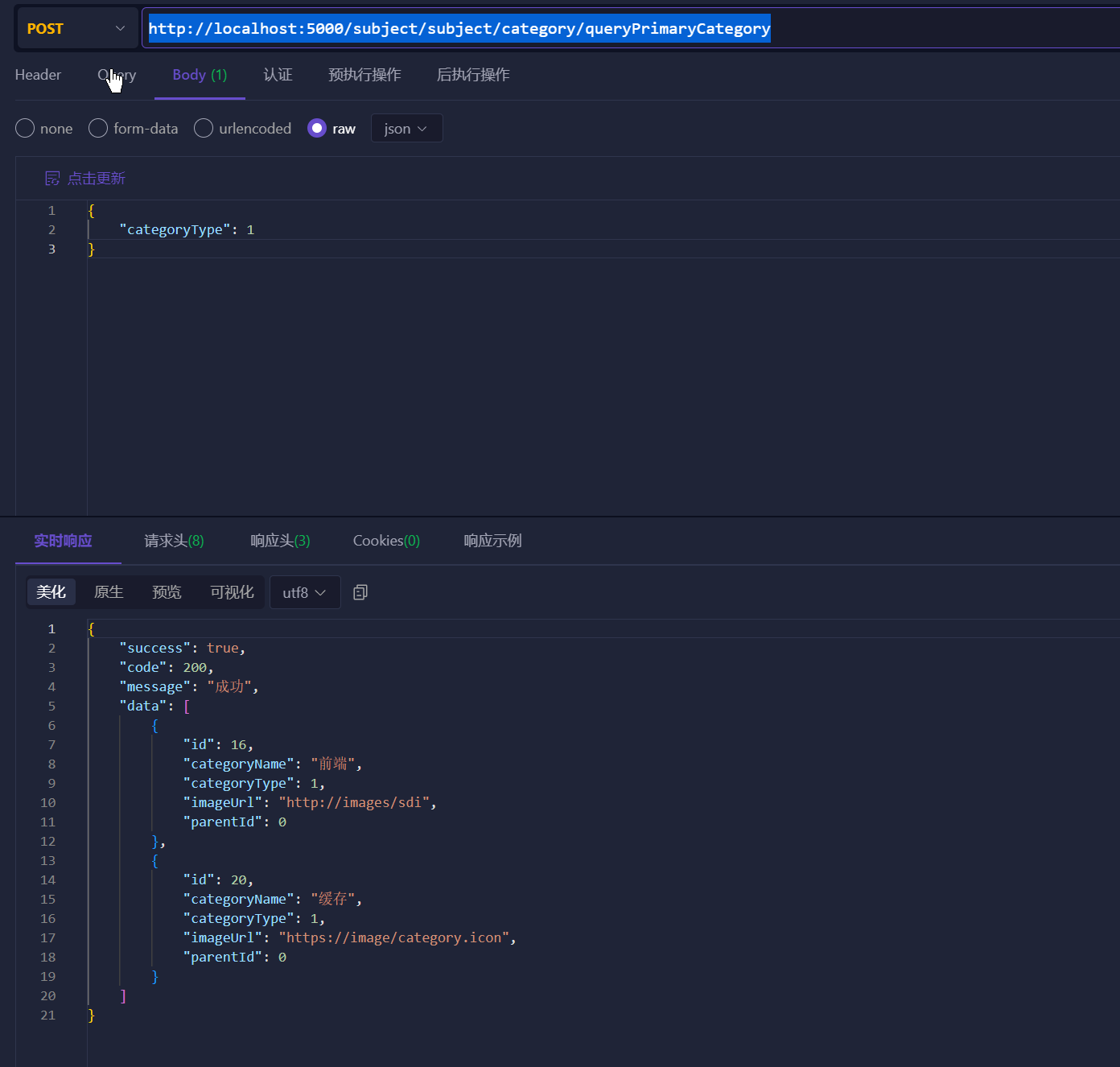
ReLU（Rectified Linear Unit）激活函数

ReLU（Rectified Linear Unit）激活函数是一种广泛应用于神经网络中的非线性激活函数。其公式如下：

$$\text{ReLU}(x)=\max (0,x)$$

在图中，你可以看到 ReLU 函数的特点：

1. 当 $x<0$ 时，$\text{ReLU}(x)=0$: 这意味着所有负输入值都被映射为 0，这也是 ReLU 无法处理负值的原因。虽然它能够处理负值，但输出总是 0。
2. 当 $x\ge 0$ 时，$\text{ReLU}(x)=x$: 这意味着正输入值保持不变，正半部分是线性的。

ReLU 激活函数的性质

1. 简单易计算：ReLU 激活函数的计算非常简单，只需要比较输入值和零的大小，然后取较大值。这使得它在计算上非常高效。

2. 非线性：尽管 ReLU 看起来像是线性的（因为正半部分是线性的），但它引入了非线性因素。这种非线性有助于神经网络学习复杂的模式。

3. 稀疏激活：由于 ReLU 函数会将负值变为零，因此它能够使得网络中的一部分神经元输出为零。这种稀疏激活可以提高模型的训练效率和泛化能力。

4. 梯度消失问题：相较于 sigmoid 和 tanh 激活函数，ReLU 缓解了梯度消失问题。sigmoid 和 tanh 在输入值极大或极小时，梯度会变得非常小，导致训练速度缓慢甚至停滞。而 ReLU 在正值区间梯度始终为1，因此在训练深络时，梯度更容易传递。

性质一：简单易计算

ReLU 激活函数的计算非常简单，只需要比较输入值和零的大小，然后取较大值。这使得它在计算上非常高效：

$$\text{ReLU}(x)=\max (0,x)$$

这种简单的计算方式使得 ReLU 在前向传播和反向传播过程中都非常快速，极大地提升了训练速度。与其他需要复杂数学运算的激活函数相比，ReLU 的实现更加高效，特别适合大型神经网络的训练。

性质二：非线性

ReLU 激活函数的公式为：
$$\text{ReLU}(x)=\max (0,x)$$

ReLU 看起来像是线性的，因为在正半部分（即 $x\ge 0$ 时），输出等于输入，表现为线性关系。然而，ReLU 实际上引入了非线性因素：

• 在负半部分（即 $x<0$ 时），输出为 0，这是一个非线性关系。
• 这种分段线性使得 ReLU 能够在神经网络中引入非线性特性，帮助模型学习复杂的模式。

性质三：稀疏激活

ReLU 函数的另一个重要性质是它能够实现稀疏激活：

$$\text{ReLU}(x)=\max (0,x)$$

这意味着，对于任何负值输入 $x$，ReLU 的输出都是 0。对于正值输入，输出等于输入值。这种特性导致了所谓的“稀疏激活”，即在某些输入条件下，网络中的很多神经元会输出 0。稀疏激活有以下几个好处：

1. 提高计算效率：

   • 当许多神经元的输出为 0 时，计算量减少，因为这些 0 值不会对下一层的计算贡献任何影响。这使得模型的 计算效率更高 ，特别是在前向传播和反向传播过程中。

2. 减少过拟合：

   • 稀疏激活起到了一种正则化的作用，防止模型过拟合。因为 只有部分神经元被激活，网络的复杂性被限制住了 ，有助于模型在训练数据上不过度拟合，从而在测试数据上表现更好。

3. 增强模型的表达能力：

   • 稀疏激活能够使得模型在 较少的参数和计算下表达复杂的非线性关系 。因为在不同的输入情况下，不同的神经元被激活，模型能够学习到更多不同的特征。

处理负值输入的局限性

虽然 ReLU 能够处理负值输入（即输入为负时输出为 0），但它 在负值区间没有输出。这意味着如果输入的数据大部分或全部是负值，ReLU 的输出将全部为 0，这会导致信息丢失并使模型无法学习。

在某些情况下，例如网络的最后一层需要处理负值（例如输出可以是正或负），使用 ReLU 作为激活函数会导致信息丢失。这是因为 ReLU 在负值区间的输出为 0，无法正确反映负值输入的信息。

为什么这与处理负值不矛盾

ReLU 的稀疏激活特性是指在数据中只有一部分输入是负值，而不是所有输入都为负值。在这种情况下，ReLU 能够利用其稀疏激活的优势：

虽然 ReLU 函数对负值输入输出为 0，似乎忽略了这些负值信息，但这并不意味着它无法处理负值输入。相反，这种处理方式带来了以下几个方面的好处：

1. 简单且有效的非线性转换：

   • 将负值输入归零是 ReLU 函数的一种简单的非线性转换方式，这种非线性有助于神经网络捕捉复杂的模式。

2. 防止梯度消失：

   • 在 Sigmoid 和 Tanh 函数中，极端输入值（非常大或非常小）会导致梯度变得非常小，导致梯度消失问题。而 ReLU 在正值区间的梯度始终为 1，这使得梯度能够顺利传播，特别是在深层网络中，这一点非常重要。

3. 选择性激活：

   • ReLU 的稀疏激活使得网络能够动态选择哪些神经元在当前输入下是重要的。这种选择性激活有助于模型专注于更重要的特征，同时抑制不重要的特征。

性质四：防止梯度消失

与 Sigmoid 和 Tanh 激活函数相比，ReLU 在防止梯度消失问题上具有显著优势。梯度消失问题是指在深层神经网络中，随着梯度在层层反向传播时逐渐减小，导致早期层的权重几乎不会更新。这会严重影响模型的训练效果。

Sigmoid 激活函数

Sigmoid 激活函数的公式为：
$$\text{sigmoid}(x)=\frac{1}{1+e^{-x}}$$

Sigmoid 函数将输入映射到 (0, 1) 的区间内，其图形呈现为一个 S 形曲线：

• 当 $x$ 很大时，$\text{sigmoid}(x)$ 接近 1。
• 当 $x$ 很小时，$\text{sigmoid}(x)$ 接近 0。
• 当 $x$ 接近 0 时，$\text{sigmoid}(x)$ 接近 0.5。

Sigmoid 函数的导数为：
$${\text{sigmoid}}^{\prime }(x)=\text{sigmoid}(x)(1-\text{sigmoid}(x))$$

可以看出，Sigmoid 函数的导数也呈现 S 形曲线：

• 当 $x$ 很大或很小时，导数接近 0。
• 当 $x$ 接近 0 时，导数接近最大值 0.25。

Tanh 激活函数

Tanh 激活函数的公式为：
$$\text{tanh}(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

Tanh 函数将输入映射到 (-1, 1) 的区间内，其图形呈现为一个中心对称的 S 形曲线：

• 当 $x$ 很大时，$\text{tanh}(x)$ 接近 1。
• 当 $x$ 很小时，$\text{tanh}(x)$ 接近 -1。
• 当 $x$ 接近 0 时，$\text{tanh}(x)$ 接近 0。

Tanh 函数的导数为：
$${\text{tanh}}^{\prime }(x)=1-{\text{tanh}}^2(x)$$

可以看出，Tanh 函数的导数也是中心对称的 S 形曲线：

• 当 $x$ 很大或很小时，导数接近 0。
• 当 $x$ 接近 0 时，导数接近最大值 1。

激活函数的比较：Sigmoid vs Tanh

1. 输出范围：

   • Sigmoid 函数的输出范围为 (0, 1)，适用于输出概率值的情况。
   • Tanh 函数的输出范围为 (-1, 1)，适用于需要输出负值的情况。

2. 均值归零：

   • Sigmoid 函数的输出非均值归零，可能导致后续层的输入偏向某一方向。
   • Tanh 函数的输出均值归零，使得后续层的输入更为平衡，有助于梯度下降的收敛。

3. 梯度消失问题：

   • Sigmoid 函数和 Tanh 函数都存在梯度消失问题，特别是在输入值绝对值较大时，导数趋近于 0。
   • Tanh 函数在一定程度上缓解了梯度消失问题，但仍然无法完全避免。

ReLU 的梯度优势

• ReLU 在正值区间的梯度始终为 1，这使得梯度能够顺利传播，特别是在深层网络中，这一点非常重要。
• 虽然 ReLU 在负值区间的梯度为 0，但这不会影响正值区间的梯度传播，因此整体上 ReLU 能有效防止梯度消失问题。

ReLU 的变种

虽然 ReLU 在很多应用中表现良好，但它也有一些缺点，如“死亡 ReLU”问题（一些神经元在训练过程中可能永远不会被激活，即输出一直为零）。为了解决这些问题，出现了很多 ReLU 的变种：

1. Leaky ReLU：
   $$\text{Leaky ReLU}(x)=\{\begin{array}{ll}x& \text{if }x\ge 0\\ \alpha x& \text{if }x<0\end{array}$$
   其中 $\alpha$ 是一个很小的正数（如 0.01）。它允许在负值区间有一个非零的输出，从而缓解“死亡 ReLU”问题。

2. Parametric ReLU (PReLU)：
   $$\text{PReLU}(x)=\{\begin{array}{ll}x& \text{if }x\ge 0\\ \alpha x& \text{if }x<0\end{array}$$
   其中 $\alpha$ 是一个可学习的参数。

3. Exponential Linear Unit (ELU)：
   $$\text{ELU}(x)=\{\begin{array}{ll}x& \text{if }x\ge 0\\ \alpha (e^x-1)& \text{if }x<0\end{array}$$
   ELU 在负值区间的输出会渐近于 $-\alpha$，从而可以缓解梯度消失问题，同时在正值区间保持了 ReLU 的优点。

ReLU 在神经网络中的应用

ReLU 被广泛应用于各类神经网络，特别是卷积神经网络（CNN）和全连接神经网络（FCN）。其简单高效的性质使得它在实际应用中表现出色。

1. 卷积神经网络（CNN）：在图像分类、目标检测等任务中，CNN 广泛采用 ReLU 作为激活函数，提高了训练速度和模型性能。
2. 全连接神经网络（FCN）：在许多分类和回归任务中，ReLU 也被广泛采用。

总的来说，ReLU 激活函数因其计算简单、有效缓解梯度消失问题和提高训练效率的特性，在深度学习中得到了广泛应用。其变种如 Leaky ReLU、PReLU 和 ELU 也在不同场景中进一步提升了模型的性能和稳定性。