主成分分析 (PCA)
PCA 是一种线性降维方法,通过投影到主成分空间,尽可能保留数据的方差。
原理
PCA 通过寻找数据投影后方差最大的方向,主成分是这些方向上的正交向量。
公式推理
- 对数据中心化:
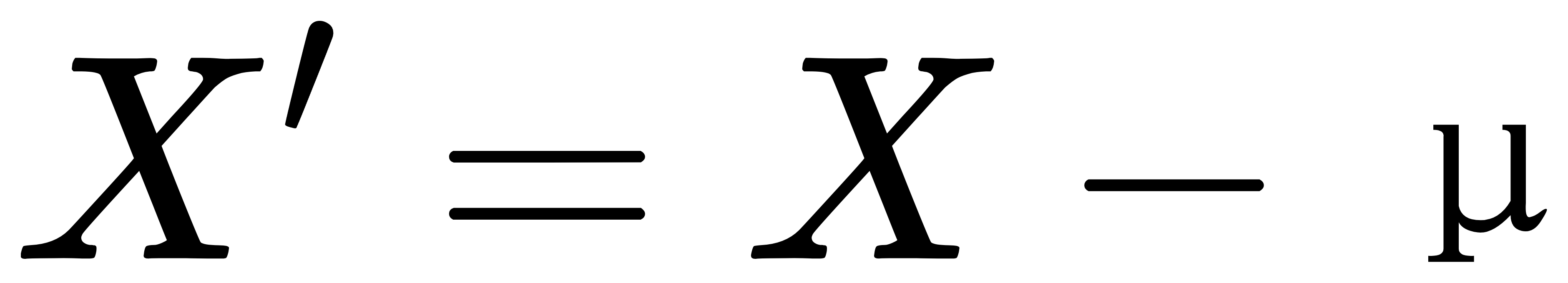
其中,μ 是数据的均值向量。
- 计算协方差矩阵:
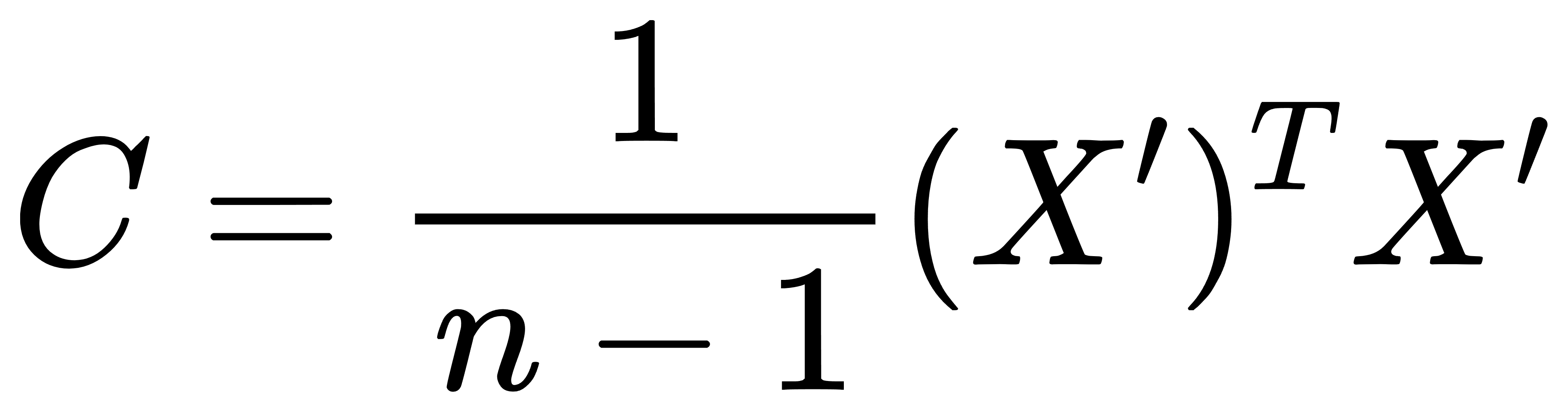
其中,n 是样本数量。
- 对协方差矩阵求特征值和特征向量:
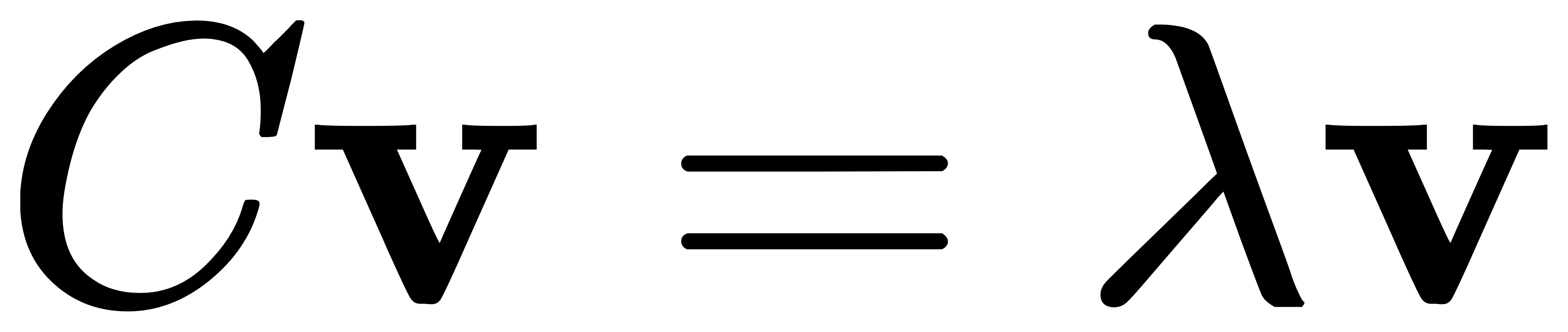
其中,v 是特征向量,λ是特征值。
- 选择前 k 个最大特征值对应的特征向量,构建投影矩阵:
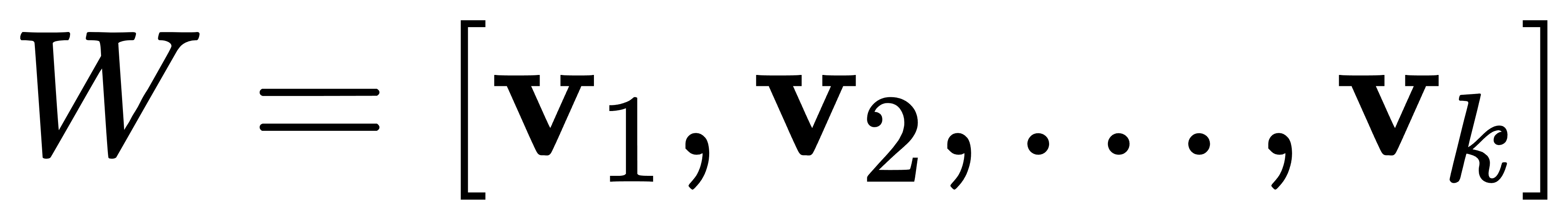
- 将原始数据投影到新的低维空间:
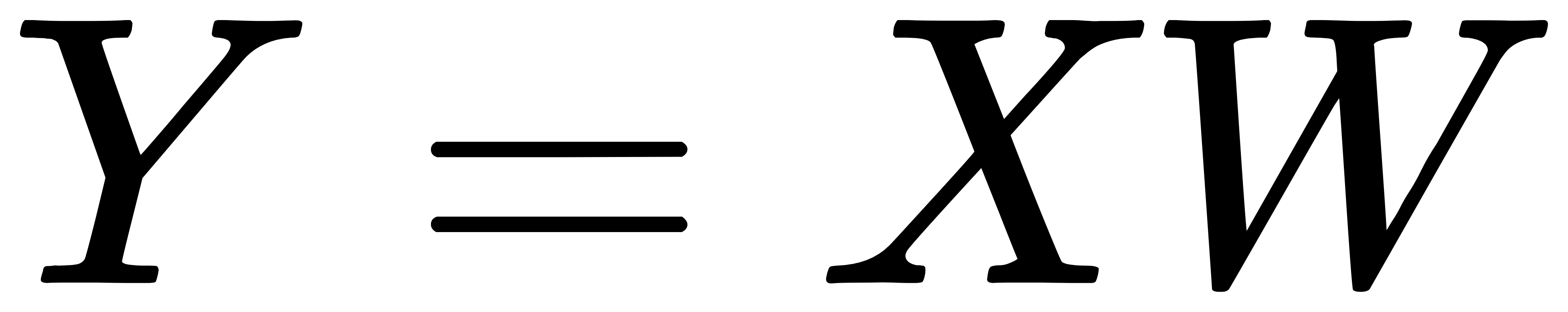
经典案例
案例:PCA在手写数字识别数据集上的应用
我们将使用经典的MNIST数据集,它包含了大量的手写数字图片,每张图片是28x28像素的灰度图像,共有10个类别(0到9)。通过PCA将MNIST数据集从784维降到2维,并可视化不同数字在降维空间的分布。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler# 加载MNIST数据集
mnist = fetch_openml('mnist_784', version=1,as_frame=False,parser='liac-arff')
X = mnist.data.astype('float64')
y = mnist.target.astype('int64')# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 使用PCA进行降维到2维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# 可视化
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='tab10', edgecolor='k', s=20)
plt.colorbar(scatter, label='Digit', ticks=range(10))
plt.title('PCA of MNIST Dataset')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.grid(True)
plt.show()代码解析
- 加载MNIST数据集:使用
fetch_openml函数加载MNIST数据集,包括特征矩阵X和目标向量y。 - 标准化数据:使用
StandardScaler对数据进行标准化处理,使得每个特征具有零均值和单位方差。 - 使用PCA进行降维:创建 PCA 对象并将数据降到 2 维。
- 可视化:绘制降维后的数据分布,不同颜色表示不同数字类别。
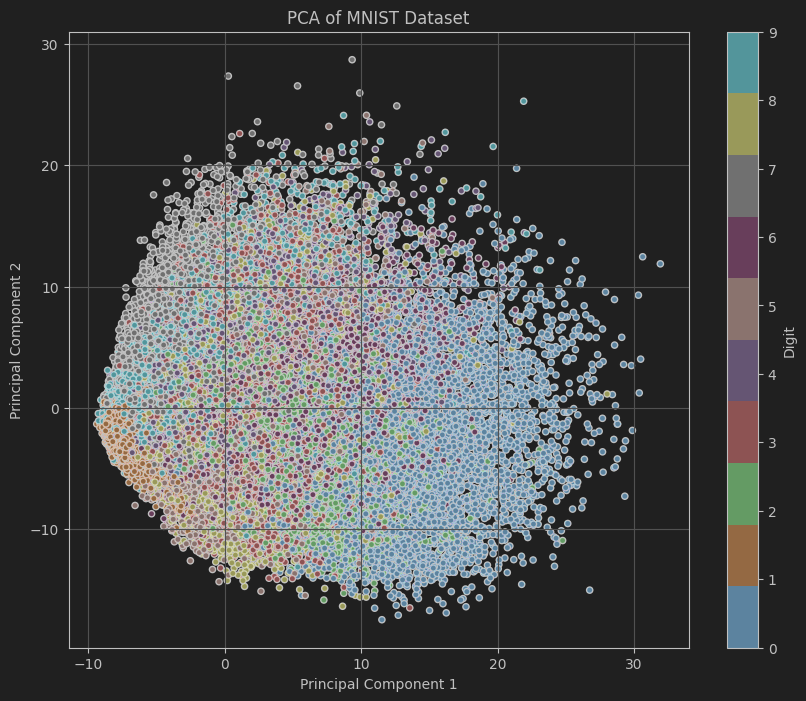
代码中展示了如何利用PCA对高维数据进行降维,并通过可视化直观地展示了降维后数据的分布情况,有助于理解数据集的结构与特征之间的关系。
线性判别分析 (LDA)
LDA 是一种监督降维方法,通过最大化类间方差与类内方差的比率,找到可以最好地区分类别的投影方向。
原理
LDA 寻找投影方向,使得同类样本的投影尽可能接近,而不同类样本的投影尽可能远离。通过类间散度矩阵和类内散度矩阵的特征值分解,确定最优投影方向。
公式推理
- 计算类内散度矩阵 SWS_WSW 和类间散度矩阵 SBS_BSB:
-
- 类内散度矩阵:
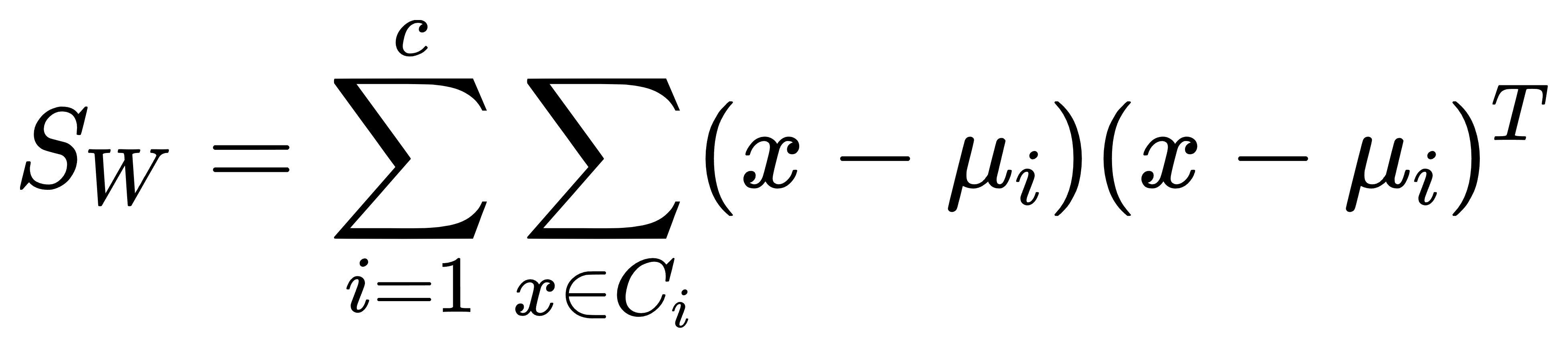
-
- 类间散度矩阵:
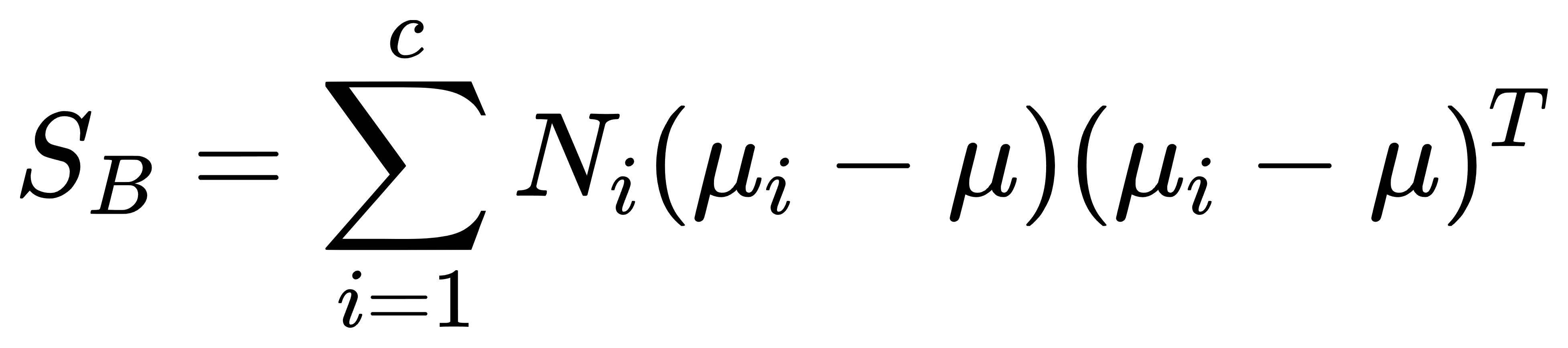
其中,μi 是第 i 类的均值向量,μ 是所有样本的总体均值向量,Ni 是第 i 类的样本数,c是类别数。
- 求解广义特征值问题:
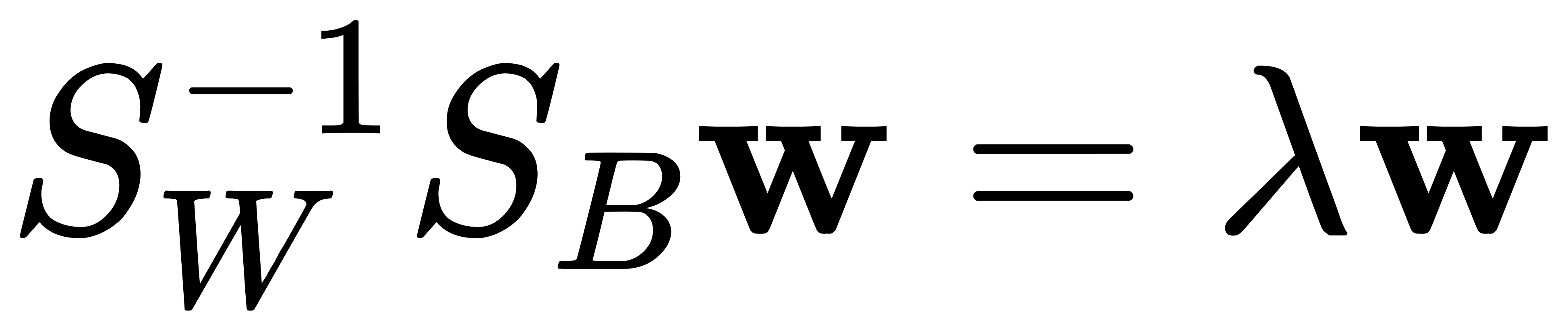
其中,w 是特征向量,λ 是特征值。
- 选择前 k 个最大特征值对应的特征向量,构建投影矩阵:
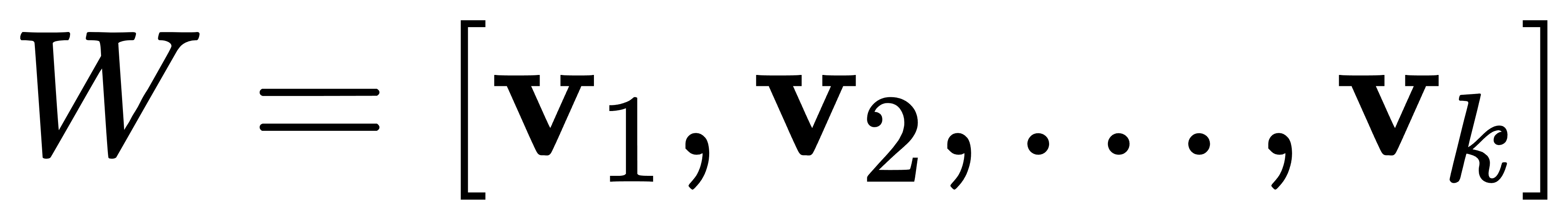
- 将原始数据投影到新的低维空间:
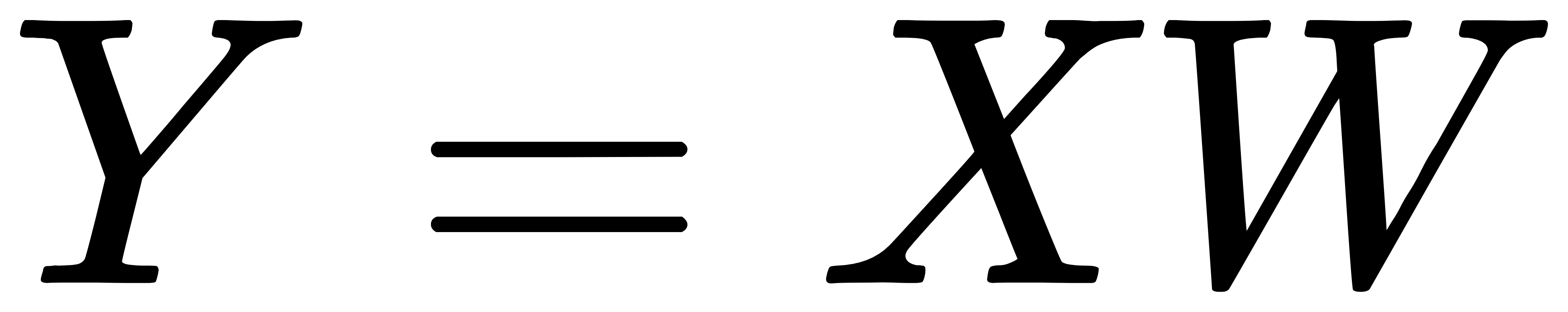
经典案例
案例:LDA 在葡萄酒分类数据集上的应用
葡萄酒数据集包含三类葡萄酒的 13 个化学特征。通过 LDA 将 13 维特征降到 2 维,并可视化不同类别葡萄酒在降维空间的分布。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA# 加载葡萄酒数据集
wine = load_wine()
X = wine.data
y = wine.target# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 使用LDA进行降维到2维
lda = LDA(n_components=2)
X_lda = lda.fit_transform(X_scaled, y)# 可视化
plt.figure(figsize=(10, 8))
for class_value in np.unique(y):plt.scatter(X_lda[y == class_value, 0], X_lda[y == class_value, 1], label=wine.target_names[class_value], edgecolor='k', s=100)
plt.xlabel('Linear Discriminant 1')
plt.ylabel('Linear Discriminant 2')
plt.title('LDA of Wine Dataset')
plt.legend()
plt.grid(True)
plt.show()代码解析
- 加载葡萄酒数据集:使用
load_wine函数加载数据集,包括特征矩阵X和目标向量y。 - 标准化数据:使用
StandardScaler对数据进行标准化处理,使得每个特征具有零均值和单位方差。 - 使用LDA进行降维:创建 LDA 对象并将数据降到 2 维。
- 可视化:绘制降维后的数据分布,不同颜色表示不同类别。
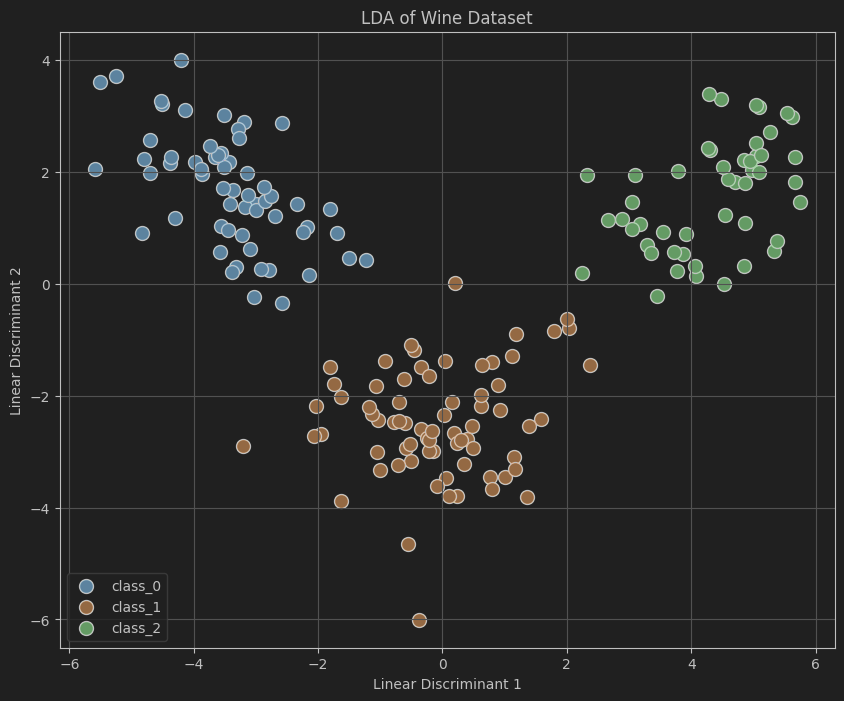
代码展示了如何利用LDA对高维数据进行降维,并通过可视化直观地展示了降维后数据的分布情况,有助于理解数据集的结构与特征之间的关系。