3.十字链表（有向图）

十字链表是有向图的一种链式存储结构。

• 不足

对于有向图来说，邻接表是有缺陷的。了解入度就必须要遍历整个图才能知道；反之，逆邻接表解决了入度却不了解出度的情况。

• 十字链表(Orthogonal List)

把邻接表与逆邻接表结合起来就是我们现在要介绍的有向图的一种存储方法：十字链表(Orthogonal List)。

顶点结点结构：

data	firstin	firstout

firstin：表示作为入边表头指针，指向该顶点的入边表中第一个结点；
firstout：表示作为出边表头指针，指向该顶点的出边表中的第一个结点。

边结点结构：

tailvex	headvex	info	headlink	taillink

tailvex：是指弧起点在顶点表的下标；
headvex：是指弧终点在顶点表中的下标；
headlink：是指入边表指针域，指向终点相同的下一条边；
taillink：是指边表指针域，指向起点相同的下一条边。

如果是网，还可以再增加一个 info 域来存储权值。

3.1性能分析

空间复杂度：顶点个数+边的个数 O(|V|+|E|)

在此把邻接表与逆邻接表结合起来，解决了存储时候，有冗余的问题，也更容易求得顶点的出度和入度。而且它除了结构复杂一点外，其实创建图算法的时间复杂度是和邻接表相同的。

4.邻接多重表（无向图）

邻接多重表是无向图的另一种链式存储结构。

• 不足

在邻接表中，容易求得顶点和边的各种信息，但每条边对应两条冗余信息。删除顶点、删除边等操作时，需要分别在两个顶点的边表中遍历，效率较低。

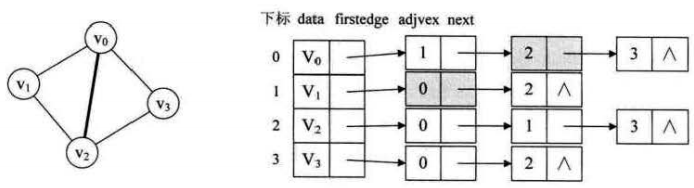
eg. 如果要删除一条边，那么在邻接表中，要在两个顶点（边的两端点）的单链表中进行边的删除。

若要删除左图的( V0 , V2 )这条边，需要对邻接表结构中右边表的阴影两个结点进行删除操作，显然这是比较烦琐的。

• 邻接多重表(adjacent multiList)

顶点结点结构：

data	firstedge

data 域存储该顶点的相关信息；
firstedge 域指示第一条依附于该顶点的边。

边结点结构：

ivex	jvex	info	ilink	jlink

ivex和jvex是与某条边依附的两个顶点在顶点表中下标。
ilink 指向依附顶点ivex的下一条边，jlink 指向依附顶点jvex的下一条边。

如果是网，还可以再增加一个 info 域来存储权值。

删除一条边，就改变它的两个link指针。

删除一个顶点，那么就把对应的边表清空。

4.1性能分析

空间复杂度：顶点个数+边的个数 O(|V|+|E|)

删除边、结点等的操作很方便。

5.边集数组

边集数组是由两个数组构成。一个是存储顶点的信息；另一个是存储边的信息。

这个边数组每个数据元素由一条边的起点下标(begin)、 终点下标(end)和权(weight)组成，如下图所示：

显然边集数组关注的是边的集合，在边集数组中要查找一个顶点的度需要扫描整个边数组，效率并不高。因此它更适合对边依次进行处理的操作，而不适合对顶点相关的操作。