12月16号,也就是今天,华为鸿蒙OS手机开发者Beta版本来啦! 发布会给出了最新版的开发环境(DevEco Studio 2.0 Beta3),支持手机等多设备模拟器的跨端运行调试,大家已经可以上手体验鸿蒙手机应用开发了,作为最早的一批鸿蒙开发人员,我真是太开心了!基于鸿蒙系统,我和小伙伴们已经有了“亿点点”成果,从今天开始,我们将陆续开源,并从以下三个方面和大家分享相关经验~
1. 全场景的应用开发
目前移动互联网的创新仍局限于手机单设备,全场景下的应用开发会成为日后的主流,而鸿蒙恰恰是为万物互联而生。
在这次手机开发者Beta 活动中,有大量合作伙伴分享生态场景案例。其实,最早华为在HDC活动中展示的教育、办公生态场景案例,就是我们和华为合作完成的。在那之后,我们基于全场景理念,还开发了更多的应用。这些应用我们都会陆续开源并且详细讲解,让广大开发者了解鸿蒙全场景分布式的应用是如何开发的。
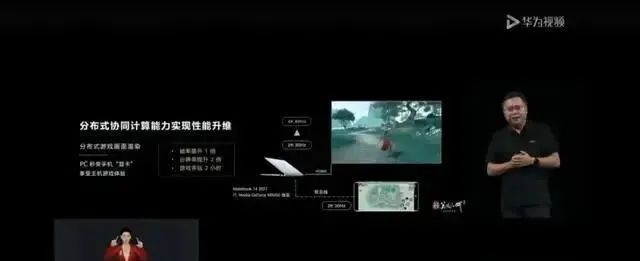
在这里我们就“智能家居美颜相机”进行简单介绍。大家是否想过家里的大屏也能像手机一样进行美颜拍照,但是大屏不具备美颜计算的能力怎么办?没关系,你的手机能够美颜就可以。在这个场景中,可以让基于鸿蒙系统的大屏调起手机的美颜能力,完成大屏美颜拍照。该项目包含了鸿蒙系统的视频编解码、通信协议、视频渲染等模块(先放上个图给大家看下效果)。

2. 开源三方组件
安卓之所以强大,不仅仅基于安卓自身的能力,还有众多的开源第三方组件生态支持,我相信有很多安卓开发的小伙伴都会去github上找一些开源的三方组件帮助自己进行应用开发吧。那么你是否想要在鸿蒙开发的过程中也有这样的组件进行支持呢?大家不必担心,我们也复现和移植了很多安卓的开源三方组件以支持鸿蒙,大家也可以像使用安卓三方组件一样去使用这些鸿蒙组件。后续,我们还会对这些组件的移植和构建方法进行介绍,有助于广大的开发者开发自己的鸿蒙组件,共同助力鸿蒙的生态建设。
我们目前已完成20余个三方件的构建,其中包含能力众多,涵盖UI增强、视频缓存等多个方面,还有大家看视频时都爱用的弹幕功能(如下图所示)。

3. 鸿蒙开发书籍
为了让广大的开发者都能够上手鸿蒙开发,我们牺牲了2厘米发际线完成了一部鸿蒙系统基本应用开发的书。这本书写的浅显易懂,简明摘要,融合我们在平时开发工作中遇到的各种难点的解决方法,是想要入坑鸿蒙应用开发小伙伴的不二之选。我们的第一本书面向初学者,不管你有没有开发经验,它都能够帮助你上手开发鸿蒙的简单应用。这本书马上就要和大家见面了,感兴趣的小伙伴记得购买哦~
后续我们还会推出进阶版本的开发书籍,主要针对鸿蒙的高阶能力和复杂场景应用,敬请期待!