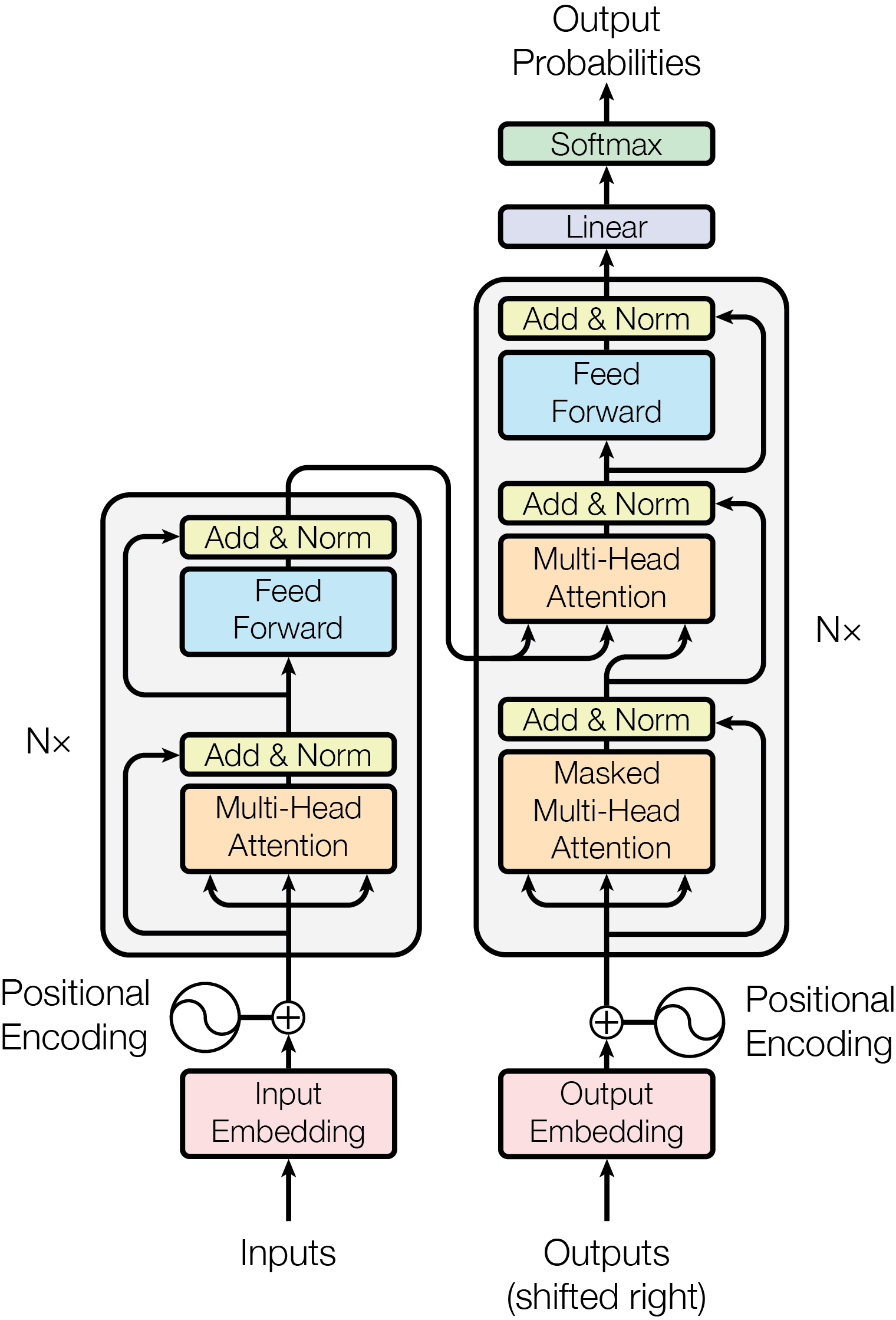
一、最长递增子序列

简单，只不过返回值不是dp数组最后一个元素了，自己做出来AC了

class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int>dp(nums.size()+1,1);for(int i=1;i<nums.size();i++){for(int j=i-1;j>=0;j--){if(nums[i]>nums[j])dp[i]=max(dp[j]+1,dp[i]);}}int max=0;for(int i=0;i<dp.size();i++){if(max<dp[i])max=dp[i];}return max;}
};

二、 最长连续递增序列

比上面那个更简单，上面还需要双指针遍历当前元素前面所有的元素，这个只需要找前一个元素

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {vector<int>dp(nums.size()+1,1);int maxresult=dp[0];for(int i=1;i<nums.size();i++){if(nums[i]>nums[i-1])dp[i]=dp[i-1]+1;if(maxresult<dp[i])maxresult=dp[i];}return maxresult;}
};

三、最长重复子数组

        （一）dp数组含义：dp[i][j]表示数组下标为i-1作为数组1的结尾，j-1作为数组2的结尾的的当前公共子数组的长度（不是i和j的原因是因为，第0个数需要第-1个数来推，下标越界）

        （二）递推公式：

                if（nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1

        （三）初始化：全为0

        （四）遍历顺序，两个数组地位相同，先遍历谁都行

        （五）dp数组

        

class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {//dp[i][j]数组1中第i个之前和数组2中第j个之前公共的长度vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1,0));int result=0;for(int i=1;i<=nums1.size();i++){for(int j=1;j<=nums2.size();j++){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;if(dp[i][j]>result)result=dp[i][j];}}return result;}
};