(DDPM) denoising diffusion probabilistic models

理论学习

本文价值

本文是 Diffusion 这一类模型的开山之作，首次证明 diffusion 模型能够生成高质量的图片，且奠定了所有后续模型的基本原理：加噪 --> 去噪。DDPM 模型的效果如下：

灵感来源

扩散模型的灵感来自于两部分，一部分是 GAN 和 VAE，另一部分是物理中的动力学（由此可见多领域知识碰撞火花多么重要）。

GAN 和 VAE： GAN 将随机高斯向量转换为图片，然后训练一个评价网络进行打分，从而指导 高斯分布--> 目标分布 的学习过程；

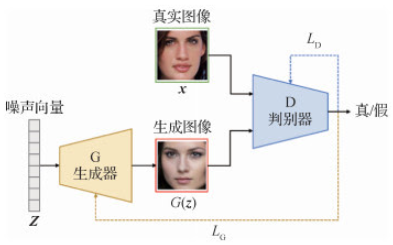
VAE 认为从 噪声向量 --> 图像的任务太难了，最好先学习一下 图像--> 噪声向量 的过程，所以 VAE 首先用编码器学习训练图片 --> 噪声向量，然后从 噪声向量 --> 目标图片。

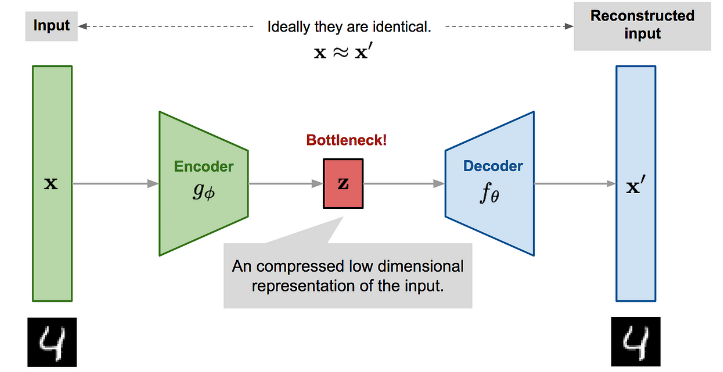
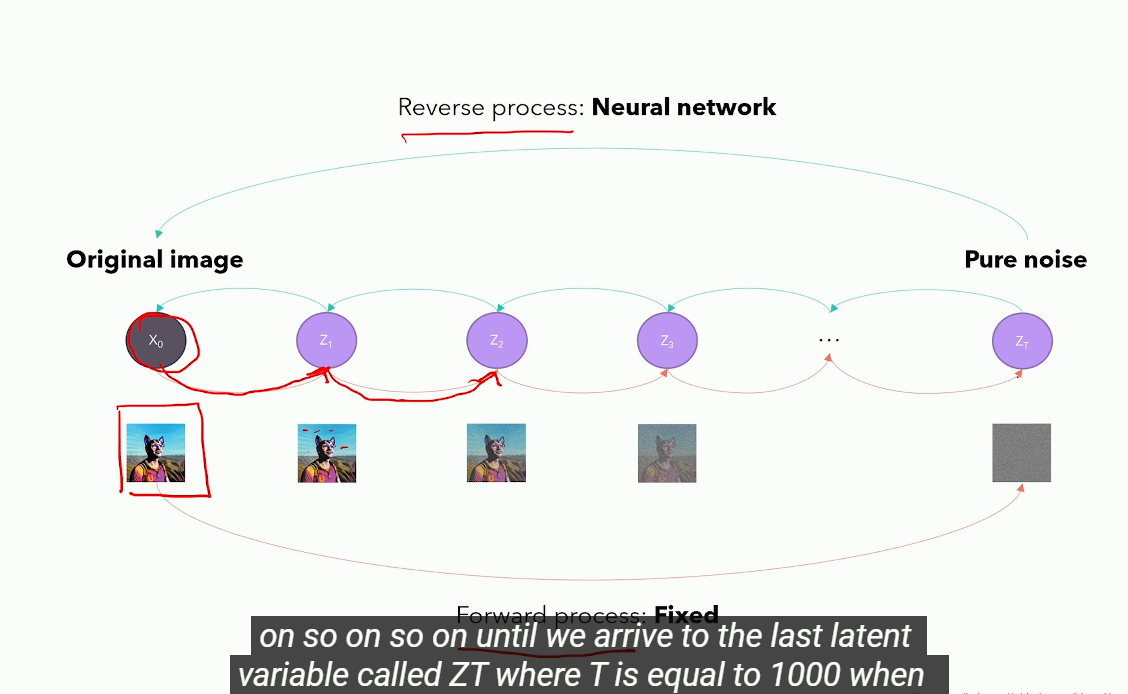
扩散模型直接将图片通过添加噪声的方式转换为 噪声图片，然后用一个网络学习 噪声图片--> 目标图片的过程。推理的时候任意采样一个高斯噪声图片，用网络转换为目标图片即可。

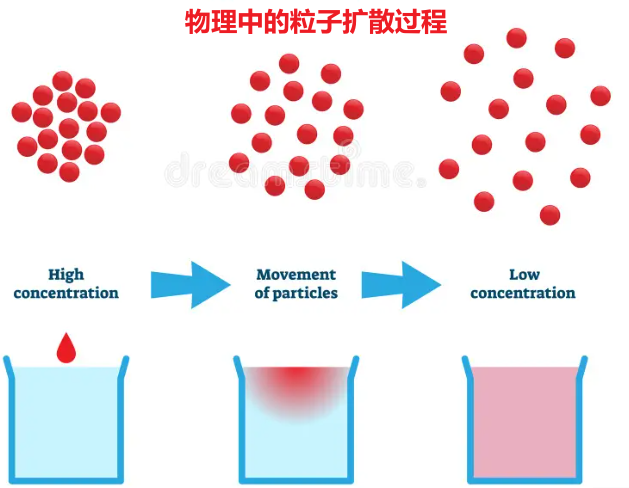
物理学的扩散过程：红墨水进入水杯 --> 红墨水缓慢移动 --> 整杯水都是红墨水

  AIGC 的扩散过程：纯噪声进入图像 --> 纯噪音逐步增强 --> 整个图片都是纯噪声

在物理学中，扩散过程描述的是粒子从高浓度区域向低浓度区域的自发性随机运动，而 Diffusion Models 将数据生成过程建模为粒子扩散过程，也就是一系列微小的、连续的随机变化过程，具体表现就是从随机噪声逐步生成真实数据的过程，就像在随机扩散过程中，分子从高浓度区域向低浓度区域移动那样。

参考资料：

1. 扩散模型(Diffusion Model)详解：直观理解、数学原理、PyTorch 实现

核心理论

前向加噪过程

这个过程将图片转换为纯高斯噪声，通过 T 步的添加高斯噪声实现。第 t-1 步到第 t 步的转换过程如下

这个公式不容易理解，因此我们将它等价为另一种表达：

其中：

是训练图片经过压缩之后的 latent image; 是 经过 t 次加噪声后得到的 latent image; 是扩散过程的最终结果，它近似于一个标准高斯噪声（0 均值，1 方差）

是在时间步 的噪声系数，通常被称为“扩散系数”，是一个很小的值，在原文中 = 0.0001， = 0.02，T = 1000

是第 t 步使用的标准高斯噪声（0 均值，1 方差）

（1）从 到 的推导

1. 初始状态：

   • 是采集得到的真实数据，假设其数据分布为

2. 逐步添加噪声：

   • 在每个时间步 ，根据以下公式从 生成 ：

     其中， 是标准正态分布的噪声。

3. 联合分布：

   • 整个前向过程的联合分布可以表示为：

（2）**直接从 生成 **

通过前向过程的定义，我们可以推导出直接从 生成 的公式：

其中， 是累积的噪声系数，定义为：

1. 定义累积噪声系数：

2. **从 ** 到 的公式：

   • 根据前向过程的定义，我们有：

     其中， 。

后向去噪过程

去噪过程是给定 求 的过程，结果也是一个高斯分布，均值和方差为 ，如下：

等式右边的三项全部已知（上面的加噪部分已经详细说明了，此处不再赘述），直接代入这个式子可以得到：

其中 就是 公式中的噪声。

训练过程

知道了均值和方差的真值，训练神经网络只差最后的问题了：该怎么设置训练的损失函数？加噪声逆操作和去噪声操作都是正态分布，网络的训练目标应该是让每对正态分布更加接近。那怎么用损失函数描述两个分布尽可能接近呢？最直观的想法，肯定是让两个正态分布的均值尽可能接近，方差尽可能接近。根据上文的分析，方差是常量，只用让均值尽可能接近就可以了。但是论文中采用了更简单的方式：直接比较预测的噪声和添加的噪声。

让我们来逐行理解一下这个算法。

第二行是指从训练集里取一个数据 。

第三行是指随机从 里取一个时刻用来训练。我们虽然要求神经网络拟合 个正态分布，但实际训练时，不用一轮预测 个结果，只需要随机预测 个时刻中某一个时刻的结果就行。

第四行指随机生成一个噪声 ，该噪声是用于执行前向过程生成 的噪声。

之后，我们把 和 传给神经网络 ，让神经网络预测随机噪声。

训练的损失函数是预测噪声和实际噪声之间的均方误差，对此损失函数采用梯度下降即可优化网络。

评测过程

第一行：xT ~ N(0, I)

这一步初始化了采样过程。xT 是从标准正态分布（均值为 0，协方差矩阵为单位矩阵 I）中采样得到的起始噪音。

第二行：for t = T, . . . , 1 do

这是一个从 T 到 1 的倒序循环，表示从最大时间步 T 开始，逐步降噪到时间步 1。

第三行：z ~ N(0, I) if t > 1, else z = 0

对于每个时间步 t，如果 t 大于 1，则从标准正态分布中采样一个噪声向量 z。如果 t 等于 1（最后一步），则 z 被设置为 0。

第四行：xt-1 = 1/√αt * (xt - (1-αt)/√(1-ᾱt) * ϵθ(xt, t)) + σt*z

这是算法的核心步骤，用于计算前一个时间步的 xt-1，

其中：xt 是当前时间步的样本

ϵθ(xt, t) 是一个神经网络，预测给定 xt 和 t 时的噪声

αt 和 ᾱt 是预定义的调度参数

σt 是噪声尺度参数

这个公式实际上是在逐步去除噪声，同时引入一些随机性以保持生成过程的多样性。

第六行：return x0

返回最终生成的样本 x0

代码实践

预览一下我们训练的 DDPM 模型的效果：

数据集

为了快速地训练和评测 diffusion 模型，我们使用最简单的手写数字识别数据集 Mnist.

# 数据加载和预处理
def load_data():
    """
    加载 MNIST 数据集并进行预处理
    :return: 训练数据加载器
    """
    # 定义图像预处理流程
    transform = transforms.Compose([
        transforms.Resize(image_size),  # 调整图像大小到指定的 image_size(int)
        transforms.ToTensor(),  # 将 PIL 图像转换为 PyTorch 张量
        transforms.Normalize((0.5,), (0.5,))  # 标准化图像,使像素值范围从[0,1]变为[-1,1]
    ])
    
    # 加载 MNIST 数据集
    dataset = datasets.MNIST(
        root='./data',  # 数据集存储路径
        train=True,  # 使用训练集
        download=True,  # 如果数据不存在,则下载
        transform=transform  # 应用上面定义的预处理流程
    )
    
    # 创建数据加载器
    dataloader = DataLoader(
        dataset,  # 要加载的数据集
        batch_size=batch_size,  # 每批加载的样本数
        shuffle=True,  # 随机打乱数据
        num_workers=4  # 使用4个子进程加载数据
    )
    
    return dataloader

模型结构

为了简单起见，没有实现 vae 图片压缩/解压，也没有 text encoder(如 CLIP )，仅实现最重要的 UNet.

与原论文保持一致，使用经典的 4 次下采样/上采样的 UNet 结构，所以要求图片尺寸是 32 的倍数即可。

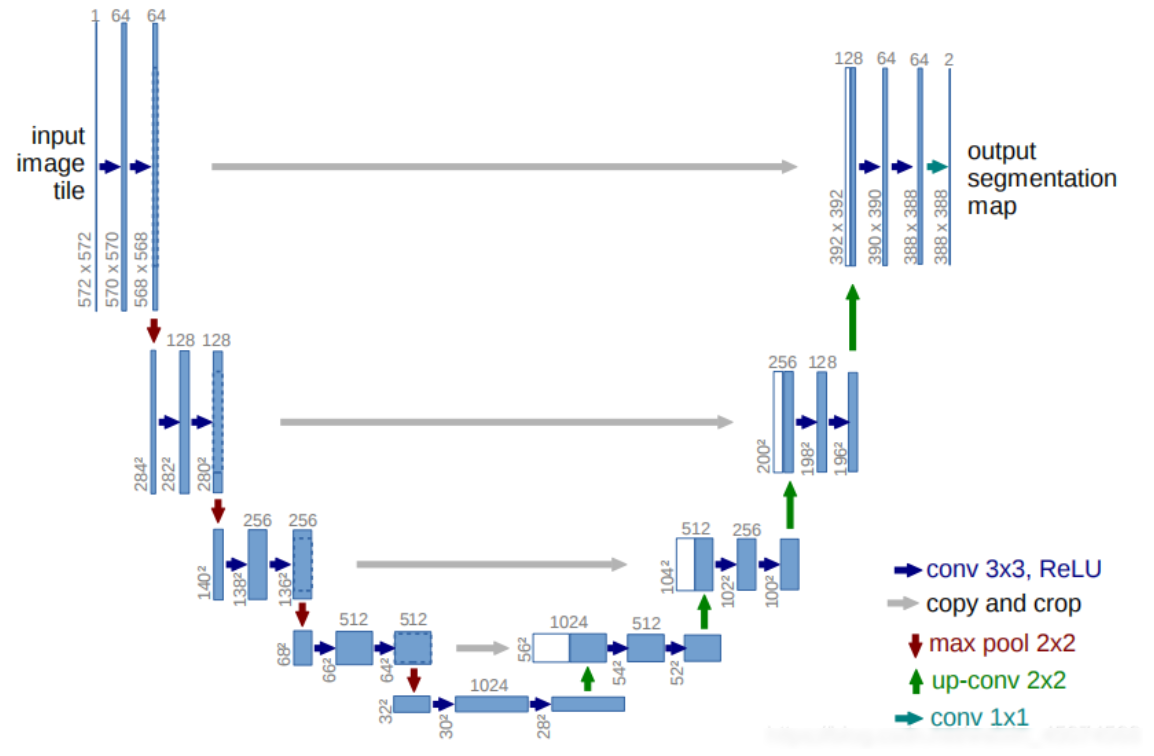
对应的代码实现：

# 定义基础的双卷积块，用于后续的 UNet
class DoubleConv(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(DoubleConv, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 3, padding=1),  # 第一个3x3卷积
            nn.BatchNorm2d(out_channels),  # 批归一化
            nn.ReLU(inplace=True),  # ReLU激活函数
            nn.Conv2d(out_channels, out_channels, 3, padding=1),  # 第二个3x3卷积
            nn.BatchNorm2d(out_channels),  # 批归一化
            nn.ReLU(inplace=True)  # ReLU激活函数
        )

    def forward(self, x):
        return self.conv(x)  # 应用两次卷积操作

# 定义条件 U-Net 模型
class ConditionalUNet(nn.Module):
    def __init__(self, out_ch=channels):
        """
        条件 U-Net 模型
        :param out_ch: 输出通道数,默认为全局变量channels
        """
        super().__init__()
        # 编码时间和标签
        self.time_embed = nn.Sequential(
            nn.Linear(1, 64),  # 将时间步编码为64维向量
            nn.SiLU(),  # SiLU激活函数
            nn.Linear(64, 128)  # 进一步编码为128维向量
        )
        self.label_embed = nn.Embedding(num_classes, 128)  # 将类别标签编码为128维向量
        
        # 编码图像
        self.enc1 = DoubleConv(channels+128, 64)  # 输入通道数为原始通道数+条件编码维度
        self.enc2 = DoubleConv(64, 128)
        self.enc3 = DoubleConv(128, 256)
        self.enc4 = DoubleConv(256, 512)
        
        # 桥接层
        self.bridge = DoubleConv(512, 1024)

        # 解码器 (上采样)
        self.dec4 = DoubleConv(1024, 512)
        self.dec3 = DoubleConv(512, 256)
        self.dec2 = DoubleConv(256, 128)
        self.dec1 = DoubleConv(128, 64)

        # 最大池化
        self.pool = nn.MaxPool2d(2)  # 2x2的最大池化

        # 转置卷积 (用于上采样)
        self.upconv4 = nn.ConvTranspose2d(1024, 512, kernel_size=2, stride=2)
        self.upconv3 = nn.ConvTranspose2d(512, 256, kernel_size=2, stride=2)
        self.upconv2 = nn.ConvTranspose2d(256, 128, kernel_size=2, stride=2)
        self.upconv1 = nn.ConvTranspose2d(128, 64, kernel_size=2, stride=2)

        # 最终输出层
        self.final = nn.Conv2d(64, out_ch, kernel_size=1)  # 1x1卷积调整通道数

    def forward(self, x, t, label):
        """
        前向传播
        :param x: 输入图像，shape为(batch_size, channels=1, height, width)
        :param t: 时间步，shape为(batch_size,)
        :param label: 标签，shape为(batch_size,)
        :return: 预测的噪声，shape与输入图像相同
        """
        t = self.time_embed(t.unsqueeze(-1).float())  # 编码时间步
        label = self.label_embed(label)  # 编码标签
        condition = (t + label).unsqueeze(-1).unsqueeze(-1)  # 合并时间和标签条件
        condition = condition.expand(-1, -1, x.shape[2], x.shape[3])  # 扩展条件到与输入图像相同的空间维度
        
        x = torch.cat([x, condition], dim=1)  # 将条件与输入图像在通道维度上拼接
        
        # 编码器部分
        enc1 = self.enc1(x)                  # (b, 64, h, w)
        enc2 = self.enc2(self.pool(enc1))    # (b, 128, h/2, w/2)
        enc3 = self.enc3(self.pool(enc2))    # (b, 256, h/4, w/4)
        enc4 = self.enc4(self.pool(enc3))    # (b, 512, h/8, w/8)
        
        # 桥接层
        bridge = self.bridge(self.pool(enc4))  # (b, 1024, h/16, w/16)
        
        # 解码器部分 (带跳跃连接)
        dec4 = self.dec4(torch.cat([self.upconv4(bridge), enc4], dim=1))  # (b, 512, h/8, w/8)
        dec3 = self.dec3(torch.cat([self.upconv3(dec4), enc3], dim=1))    # (b, 256, h/4, w/4)
        dec2 = self.dec2(torch.cat([self.upconv2(dec3), enc2], dim=1))    # (b, 128, h/2, w/2)
        dec1 = self.dec1(torch.cat([self.upconv1(dec2), enc1], dim=1))    # (b, 64, h, w)
        
        out = self.final(dec1)  # 最终输出
        
        return out

训练&推理

每个 train_step 中首先随机挑选 t, 生成对应的噪声和 x_t，然后用 unet 预测噪声，然后比较 gt 噪声和预测噪声的 L2 loss 作为训练的 loss, 如下：

def train_step(self, x0, labels):
    """
    训练步骤
    :param x0: 原始图像，shape为(batch_size, channels, height, width)
    :param labels: 图像标签，shape为(batch_size,)
    :return: 损失值
    """
    t = torch.randint(0, time_steps, (x0.shape[0],), device=device).long()
    xt, noise = self.forward_diffusion(x0, t)
    predicted_noise = self.model(xt, t / time_steps, labels)
    loss = F.mse_loss(noise, predicted_noise)
    return loss

推理过程如下：

代码实现如下：

@torch.no_grad()
def sample(self, n_samples, labels, size=image_size):
    """
    从模型中采样生成图像
    :param n_samples: 生成图像的数量
    :param labels: 标签，shape为(n_samples,)，值为0-9之间的整数
    :param size: 生成图像的大小
    :return: 生成的图像，shape为(n_samples, channels, size, size)
    """
    self.model.eval()
    x = torch.randn(n_samples, channels, size, size).to(device)

    for i in reversed(range(time_steps)):
        t = torch.full((n_samples,), i, device=device, dtype=torch.long)
        predicted_noise = self.model(x, t / time_steps, labels)
        alpha = self.alphas[i]
        alpha_cumprod = self.alphas_cumprod[i]
        beta = self.betas[i]

        if i > 0:
            noise = torch.randn_like(x)
        else:
            noise = torch.zeros_like(x)

        x = (1 / torch.sqrt(alpha)) * (x - ((1 - alpha) / torch.sqrt(1 - alpha_cumprod)) * predicted_noise) + torch.sqrt(beta) * noise

    self.model.train()
    x = (x.clamp(-1, 1) + 1) / 2
    return x

整体代码

所有的代码集成如下：

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt

# 设置设备和超参数
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 训练的总轮数
num_epochs = 100
# 每批处理的样本数
batch_size = 128
# 图像的大小（宽度和高度）
image_size = 32
# 图像的通道数（MNIST为灰度图像，所以是1）
channels = 1
# 扩散过程的时间步数
time_steps = 1000
# β调度的起始值（控制噪声添加的速率）
beta_start = 0.0001
# β调度的结束值
beta_end = 0.02
# 类别数量（MNIST数据集有10个数字类别）
num_classes = 10

class DoubleConv(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(DoubleConv, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 3, padding=1),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(out_channels, out_channels, 3, padding=1),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True)
        )

    def forward(self, x):
        return self.conv(x)

# 定义条件 U-Net 模型
class ConditionalUNet(nn.Module):
    def __init__(self, out_ch=channels):
        """
        条件 U-Net 模型
        """
        super().__init__()
        # encode time and labels
        self.time_embed = nn.Sequential(
            nn.Linear(1, 64),
            nn.SiLU(),
            nn.Linear(64, 128)
        )
        self.label_embed = nn.Embedding(num_classes, 128)
        
        # encode images
        self.enc1 = DoubleConv(channels+128, 64)
        self.enc2 = DoubleConv(64, 128)
        self.enc3 = DoubleConv(128, 256)
        self.enc4 = DoubleConv(256, 512)
        
        # Bridge
        self.bridge = DoubleConv(512, 1024)

        # Decoder (Upsampling)
        self.dec4 = DoubleConv(1024, 512)
        self.dec3 = DoubleConv(512, 256)
        self.dec2 = DoubleConv(256, 128)
        self.dec1 = DoubleConv(128, 64)

        # Max pooling
        self.pool = nn.MaxPool2d(2)

        # Transposed convolutions
        self.upconv4 = nn.ConvTranspose2d(1024, 512, kernel_size=2, stride=2)
        self.upconv3 = nn.ConvTranspose2d(512, 256, kernel_size=2, stride=2)
        self.upconv2 = nn.ConvTranspose2d(256, 128, kernel_size=2, stride=2)
        self.upconv1 = nn.ConvTranspose2d(128, 64, kernel_size=2, stride=2)

        # Final layer
        self.final = nn.Conv2d(64, out_ch, kernel_size=1)

    def forward(self, x, t, label):
        """
        前向传播
        :param x: 输入图像，shape为(batch_size, channels=1, height, width)
        :param t: 时间步，shape为(batch_size,)
        :param label: 标签，shape为(batch_size,)
        :return: 预测的噪声，shape与输入图像相同
        """
        t = self.time_embed(t.unsqueeze(-1).float())
        label = self.label_embed(label)
        condition = (t + label).unsqueeze(-1).unsqueeze(-1)
        condition = condition.expand(-1, -1, x.shape[2], x.shape[3])
        
        x = torch.cat([x, condition], dim=1) # get (b, c+embed_dim, h, w)
        enc1 = self.enc1(x)                  # get (b, 64, h, w)
        enc2 = self.enc2(self.pool(enc1))    # get (b, 128, h/2, w/2)
        enc3 = self.enc3(self.pool(enc2))    # get (b, 256, h/4, w/4)
        enc4 = self.enc4(self.pool(enc3))    # get (b, 512, h/8, w/8)
        bridge = self.bridge(self.pool(enc4))# get (b, 1024, h/16, w/16)
        dec4 = self.dec4(torch.cat([self.upconv4(bridge), enc4], dim=1))  # get (b, 1024, h/8, w/8)
        dec3 = self.dec3(torch.cat([self.upconv3(dec4), enc3], dim=1))  # get (b, 512, h/4, w/4)
        dec2 = self.dec2(torch.cat([self.upconv2(dec3), enc2], dim=1))  # get (b, 256, h/2, w/2)
        dec1 = self.dec1(torch.cat([self.upconv1(dec2), enc1], dim=1))  # get (b, 128, h, w)
        out = self.final(dec1)
        
        return out

# 定义 Diffusion Model
class DiffusionModel:
    def __init__(self):
        """
        初始化 Diffusion Model
        """
        self.model = ConditionalUNet().to(device)
        self.betas = torch.linspace(beta_start, beta_end, time_steps).to(device)
        self.alphas = 1 - self.betas
        self.alphas_cumprod = torch.cumprod(self.alphas, dim=0)

    def get_index_from_list(self, vals, t, x_shape):
        """
        从 alphas_cumprod 列表中获取指定时间步的值
        :param vals: alphas_cumprod 列表, (T,) 
        :param t: 时间步，(batch_size,)
        :param x_shape: 输出形状
        :return: 指定时间步的值，shape与x_shape相同
        """
        batch_size = t.shape[0]
        out = vals.gather(-1, t) # 批量从 vals 中取出对应 t 的值
        out = out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device) # from (batch_size) to (batch_size,1,1,1)
        return out

    def forward_diffusion(self, x0, t):
        """
        前向扩散过程
        :param x0: 原始图像，shape为(batch_size, channels, height, width)
        :param t: 时间步，shape为(batch_size,)
        :return: 加噪后的图像和噪声，shape与x0相同
        """
        noise = torch.randn_like(x0)
        alphas_cumprod_t = self.get_index_from_list(self.alphas_cumprod, t, x0.shape)
        xt = torch.sqrt(alphas_cumprod_t) * x0 + torch.sqrt(1 - alphas_cumprod_t) * noise
        return xt, noise

    def train_step(self, x0, labels):
        """
        训练步骤
        :param x0: 原始图像，shape为(batch_size, channels, height, width)
        :param labels: 图像标签，shape为(batch_size,)
        :return: 损失值
        """
        t = torch.randint(0, time_steps, (x0.shape[0],), device=device).long()
        xt, noise = self.forward_diffusion(x0, t)
        predicted_noise = self.model(xt, t / time_steps, labels)
        loss = F.mse_loss(noise, predicted_noise)
        return loss

    @torch.no_grad()
    def sample(self, n_samples, labels, size=image_size):
        """
        从模型中采样生成图像
        :param n_samples: 生成图像的数量
        :param labels: 标签，shape为(n_samples,)，值为0-9之间的整数
        :param size: 生成图像的大小
        :return: 生成的图像，shape为(n_samples, channels, size, size)
        """
        self.model.eval()
        x = torch.randn(n_samples, channels, size, size).to(device)

        for i in reversed(range(time_steps)):
            t = torch.full((n_samples,), i, device=device, dtype=torch.long)
            predicted_noise = self.model(x, t / time_steps, labels)
            alpha = self.alphas[i]
            alpha_cumprod = self.alphas_cumprod[i]
            beta = self.betas[i]

            if i > 0:
                noise = torch.randn_like(x)
            else:
                noise = torch.zeros_like(x)

            x = (1 / torch.sqrt(alpha)) * (x - ((1 - alpha) / torch.sqrt(1 - alpha_cumprod)) * predicted_noise) + torch.sqrt(beta) * noise

        self.model.train()
        x = (x.clamp(-1, 1) + 1) / 2
        return x

# 数据加载和预处理
def load_data():
    """
    加载 MNIST 数据集并进行预处理
    :return: 训练数据加载器
    """
    # 定义图像预处理流程
    transform = transforms.Compose([
        transforms.Resize(image_size),  # 调整图像大小到指定的 image_size
        transforms.ToTensor(),  # 将 PIL 图像转换为 PyTorch 张量
        transforms.Normalize((0.5,), (0.5,))  # 标准化图像,使像素值范围从[0,1]变为[-1,1]
    ])
    
    # 加载 MNIST 数据集
    dataset = datasets.MNIST(
        root='./data',  # 数据集存储路径
        train=True,  # 使用训练集
        download=True,  # 如果数据不存在,则下载
        transform=transform  # 应用上面定义的预处理流程
    )
    
    # 创建数据加载器
    dataloader = DataLoader(
        dataset,  # 要加载的数据集
        batch_size=batch_size,  # 每批加载的样本数
        shuffle=True,  # 随机打乱数据
        num_workers=4  # 使用4个子进程加载数据
    )
    
    return dataloader

# 训练函数
def train(model, dataloader, num_epochs):
    """
    训练 Diffusion Model
    :param model: Diffusion Model 实例
    :param dataloader: 数据加载器
    :param num_epochs: 训练轮数
    """
    optimizer = torch.optim.Adam(model.model.parameters(), lr=1e-4)
    
    for epoch in range(num_epochs):
        for batch, (images, labels) in enumerate(dataloader):
            images = images.to(device)
            labels = labels.to(device)
            optimizer.zero_grad()
            loss = model.train_step(images, labels)
            loss.backward()
            optimizer.step()

            if batch % 100 == 0:
                print(f"Epoch [{epoch+1}/{num_epochs}], Batch [{batch}/{len(dataloader)}], Loss: {loss.item():.4f}")

        # 每个 epoch 结束后生成一些样本
        if (epoch + 1) % 10 == 0:
            labels = torch.arange(10).to(device)
            samples = model.sample(10, labels)
            save_samples(samples, f"samples_epoch_{epoch+1}.png")

def save_samples(samples, filename):
    """
    保存生成的样本图像
    :param samples: 生成的样本，shape为(n_samples, channels, height, width)
    :param filename: 保存的文件名
    """
    samples = samples.cpu().numpy()
    fig, axes = plt.subplots(2, 5, figsize=(10, 4))
    for i, ax in enumerate(axes.flatten()):
        ax.imshow(samples[i].squeeze(), cmap='gray')
        ax.axis('off')
        ax.set_title(f"Label: {i}")
    plt.tight_layout()
    plt.savefig(filename)
    plt.close()

# 主函数
if __name__ == "__main__":
    dataloader = load_data()
    diffusion_model = DiffusionModel()
    train(diffusion_model, dataloader, num_epochs)

    # 生成最终样本
    labels = torch.arange(10).to(device)
    final_samples = diffusion_model.sample(10, labels)
    save_samples(final_samples, "final_samples.png")

直接执行上述代码，训练 100 个 epoch, 观察到 loss 从 1.0 左右下降到 0.1 左右，则说明模型成功收敛。推理效果如下：

至此一小时结束，我们成功训练并评测了第一个 diffusion 模型！ 对更多的 AI 技术感兴趣？扫描下方二维码关注公众号获取更多干货。