生信机器学习入门4 - scikit-learn训练逻辑回归（LR）模型和支持向量机（SVM）模型

通过逻辑回归（logistic regression）建立分类模型

1.1 逻辑回归可视化和条件概率

激活函数 (activation function)：一种函数（如 ReLU 或 S 型函数），用于对上一层的所有输入进行求加权和，然后生成一个输出值（通常为非线性值）传递给下一层。

Sigmoid函数是一个在生物学中常见的S型函数，常被用作神经网络的激活函数，将变量映射到[0,1]之间，函数公式如下：
Simoid函数公式

import matplotlib.pyplot as plt
import numpy as np# 激活函数
def sigmoid(z):return 1.0 / (1.0 + np.exp(-z))# 生成从-7开始到7（但不包括7）且步长为0.1的等差数列
z = np.arange(-7, 7, 0.1)
# 使用激活函数sigmoid将上述等差数量映射到0-1
sigma_z = sigmoid(z)# 绘图
plt.plot(z, sigma_z)
plt.axvline(0.0, color='k')
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\sigma (z)$')# Y轴坐标间隔和范围
plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca()
# Y轴添加网格线
ax.yaxis.grid(True)plt.tight_layout()
plt.show()

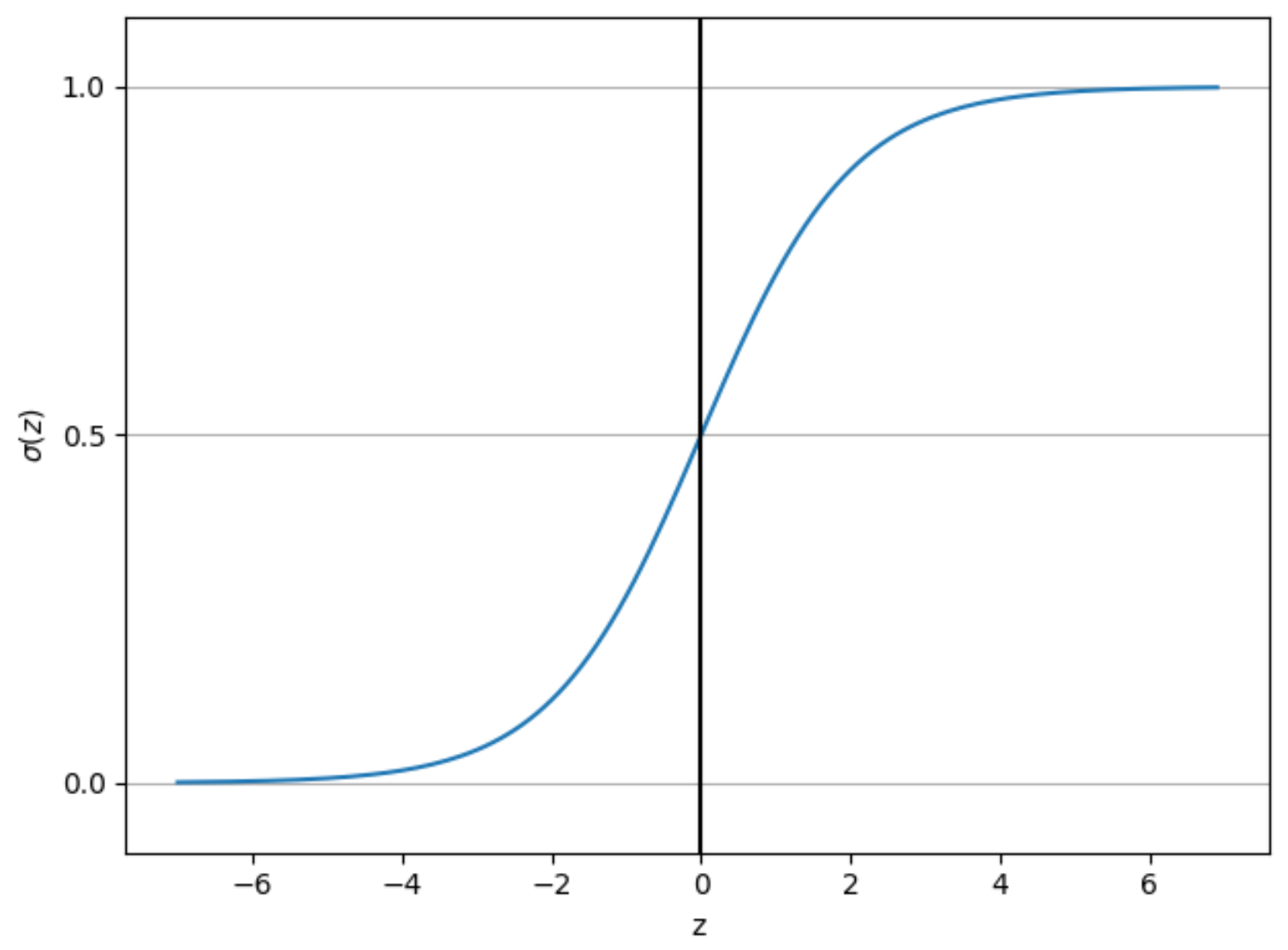
sigmoid激活函数可视化

1.2 逻辑回归工作流程图

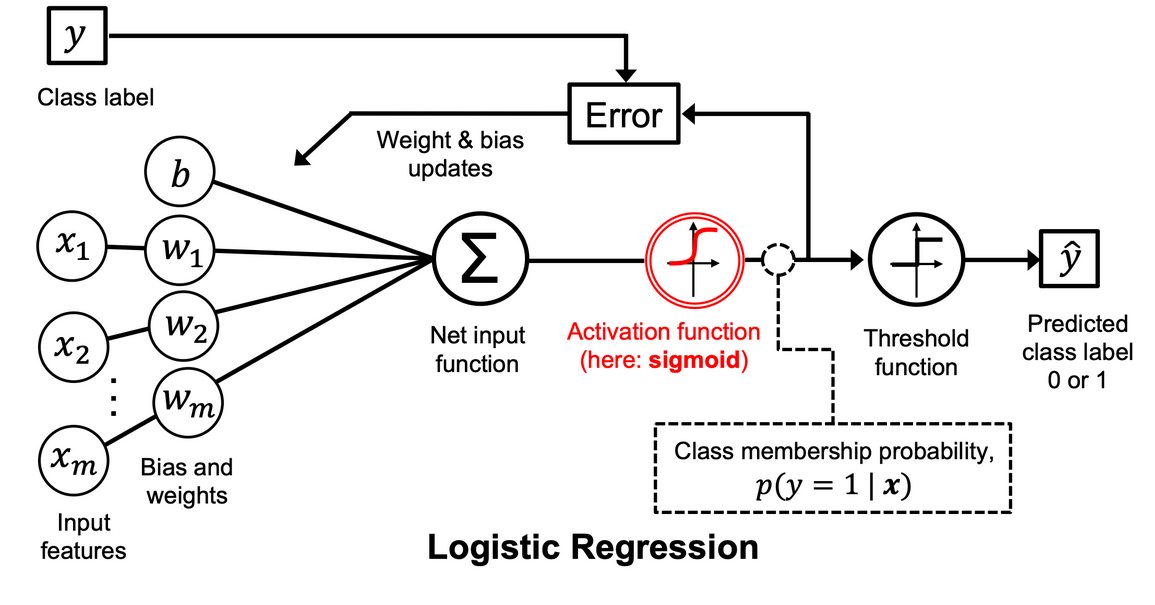
逻辑回归工作流程

1.3 逻辑损失函数的权重

损失 (Loss)：一种衡量模型的预测结果与偏离真实标签的衡量指标，例如在线性回归模型中通常采用均方误差作为loss function， 逻辑回归模型则使用对数损失函数作为loss function。

# 定义2个对数损失函数
def loss_0(z):return - np.log(1 - sigmoid(z))def loss_1(z):return - np.log(sigmoid(z))z = np.arange(-10, 10, 0.1)
sigma_z = sigmoid(z)# loss_0函数可视化
c0 = [loss_0(x) for x in z]
plt.plot(sigma_z, c0, linestyle='--', label='L(w, b) with loss_0')# loss_1函数可视化
c1 = [loss_1(x) for x in z]
plt.plot(sigma_z, c1, label='L(w, b) with loss_1')plt.ylim(0.0, 5.1)
plt.xlim([0, 1])
plt.xlabel('$\sigma(z)$')
plt.ylabel('L(w, b)')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

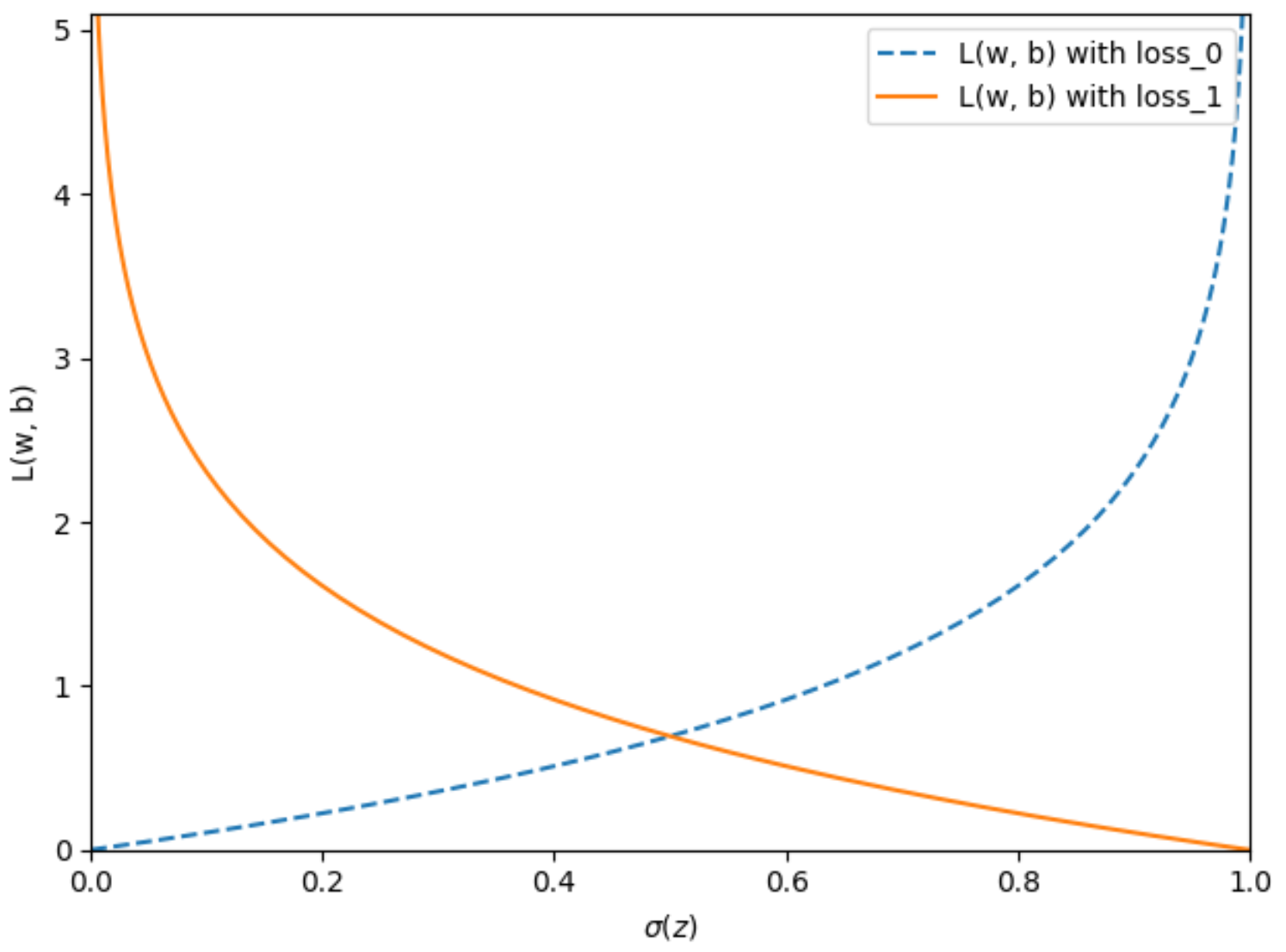
对数损失函数可视化

2. 基于梯度下降算法的逻辑回归分类器模型

批次 (batch)：机器学习模型训练的一次迭代（即完成一次梯度更新）中使用的样本集。

批次规模 (batch size)：一个批次batch中的样本数，例如SGD 的批次规模为 1，而小批次的规模通常介于 10 到 1000 之间，在模型训练时batch size通常时固定的。

周期 (epoch):在训练时，整个数据集的一次完整遍历，以便不漏掉任何一个样本。即epoch = sample number / batch size，其中sample number为样本总数，batch size为批次规模。

# 定义类
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
from distutils.version import LooseVersion
import matplotlib.pyplot as plt
import numpy as npclass LogisticRegressionGD:"""参数------------eta : floatLearning rate ：学习速率（0-1之间）n_iter : int传递训练数据集个数，即批次规模random_state : int随机数种子生成器权重属性-----------w_ : 1d-array训练权重b_ : Scalarfitting偏差.losses_ : list每个周期的逻辑回归函数数值."""def __init__(self, eta=0.01, n_iter=50, random_state=1):# 默认学习速率0.01， 批次规模50个样本self.eta = etaself.n_iter = n_iterself.random_state = random_statedef fit(self, X, y):""" 适配训练数据参数----------X : {array-like}, shape = [n_examples, n_features]训练向量，n_examples表示样本数量，n_features 表示特征数量y : array-like, shape = [n_examples]分类标签向量，包含真实的样本标签返回值-------LogisticRegressionGD实例"""rgen = np.random.RandomState(self.random_state)# 生成一个正态分布的随机数组，并将其赋值给 self.w_# loc=0.0 表示正态分布的均值（mean）是 0.0# scale=0.01 表示正态分布的标准差（standard deviation）是 0.01# size=X.shape[1] 表示生成的随机数组的大小（即长度或元素数量）应该与输入数据 X 的特征数量（列数）相同self.w_ = rgen.normal(loc=0.0, scale=0.01, size=X.shape[1])self.b_ = np.float_(0.)self.losses_ = []for i in range(self.n_iter):net_input = self.net_input(X)output = self.activation(net_input)errors = (y - output)self.w_ += self.eta * X.T.dot(errors) / X.shape[0]self.b_ += self.eta * errors.mean()loss = (-y.dot(np.log(output)) - (1 - y).dot(np.log(1 - output))) / X.shape[0]self.losses_.append(loss)return selfdef net_input(self, X):"""计算神经网络输入值，返回2个数组的点积+b_"""return np.dot(X, self.w_) + self.b_def activation(self, z):"""计算逻辑回归激活函数结果"""# 通过np.clip(z, -250, 250)将z数值限制在-250~250之间，防止溢出return 1. / (1. + np.exp(-np.clip(z, -250, 250)))def predict(self, X):"""返回分类标签预测结果，激活函数结果大于等于0.5则分类为标签1，否则为0"""return np.where(self.activation(self.net_input(X)) >= 0.5, 1, 0)def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):# 绘图图形和颜色生成markers = ('o', 's', '^', 'v', '<')colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')cmap = ListedColormap(colors[:len(np.unique(y))])# 绘图x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),np.arange(x2_min, x2_max, resolution))lab = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)lab = lab.reshape(xx1.shape)plt.contourf(xx1, xx2, lab, alpha=0.3, cmap=cmap)plt.xlim(xx1.min(), xx1.max())plt.ylim(xx2.min(), xx2.max())# 图加上分类样本for idx, cl in enumerate(np.unique(y)):plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],alpha=0.8, c=colors[idx],marker=markers[idx], label=f'Class {cl}', edgecolor='black')# 高亮显示测试数据集样本if test_idx:X_test, y_test = X[test_idx, :], y[test_idx]plt.scatter(X_test[:, 0],X_test[:, 1],c='none',edgecolor='black',alpha=1.0,linewidth=1,marker='o',s=100, label='Test set')

2.1 Iris数据集数据预处理

from sklearn import datasets
import numpy as np
####### 获取iris数据集 ####### 
iris = datasets.load_iris()
# 提取dataframe的第3列和第4列数据
X = iris.data[:, [2, 3]]
# 分类标签
y = iris.target# 打印分类标签
print('Class labels:', np.unique(y))
# Class labels: [0 1 2]####### 划分数据集 ####### 
from sklearn.model_selection import train_test_split
# X_train， y_train为训练集数据和标签
# X_test， y_test为测试集数据和标签
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)# 打印各标签的数据包含的数据数量
print('Labels counts in y:', np.bincount(y))
print('Labels counts in y_train:', np.bincount(y_train))
print('Labels counts in y_test:', np.bincount(y_test))
# Labels counts in y: [50 50 50]
# Labels counts in y_train: [35 35 35]
# Labels counts in y_test: [15 15 15]####### 标准化 ####### 
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
# 标准化训练数据X_train_std ， X_test_std 
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)####### 获取模型训练数据集 ####### 
X_train_01_subset = X_train_std[(y_train == 0) | (y_train == 1)]
y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]# 初始化类，定义学习率和批次规模参数
lrgd = LogisticRegressionGD(eta=0.3, n_iter=1000, random_state=1)
lrgd.fit(X_train_01_subset,y_train_01_subset)# 绘图
plot_decision_regions(X=X_train_01_subset, y=y_train_01_subset,classifier=lrgd)plt.xlabel('Petal length [standardized]')
plt.ylabel('Petal width [standardized]')
plt.legend(loc='upper left')plt.tight_layout()
plt.show()

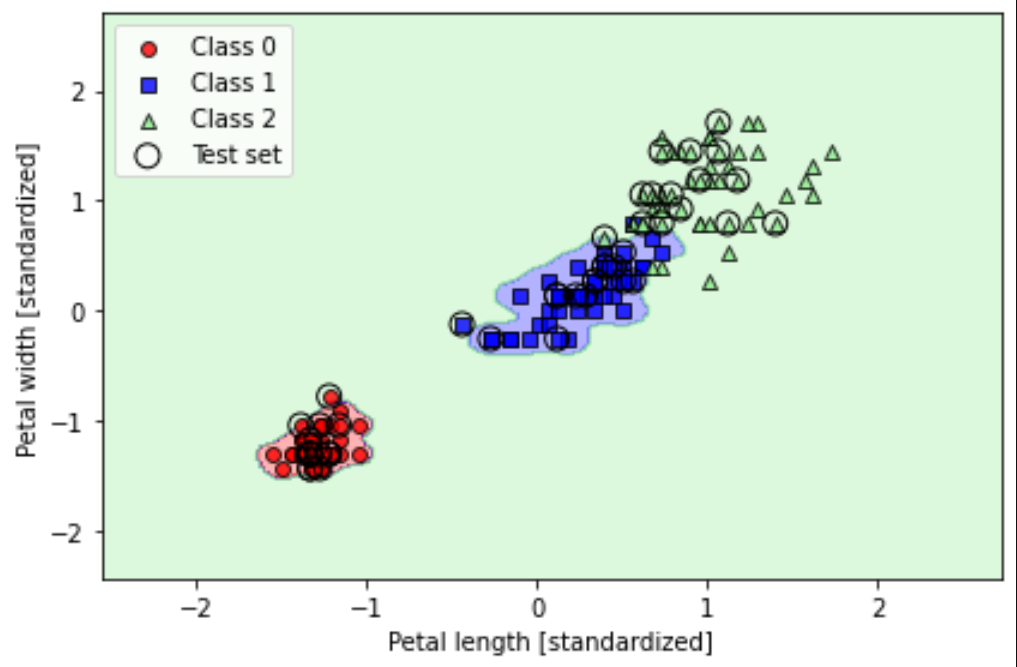
基于梯度下降算法的逻辑回归分类模型预测结果：

从下图结果可以看出，在训练数据集上，模型预测的样本标签Class0和Class1结果全部正确，但在区分表现Class1和Class2时很糟糕。

# 获取在测试数据集上模型的预测错误样本数量和预测精确度
# 将0和1替换为1和2,即可获取Class1和Class2预测结果
X_test_01_subset = X_test_std[(y_test == 0) | (y_test == 1)]
y_test_01_subset = y_test[(y_test== 0) | (y_test == 1)]y_test_pred = lrgd.predict(X_test_01_subset)
print('Misclassified examples: %d' % (y_test_01_subset != y_test_pred).sum())
# Misclassified examples: 0# 获取模型精确度
from sklearn.metrics import accuracy_score
print('Accuracy: %.3f' % accuracy_score(y_test_01_subset, y_test_pred))
# Accuracy: 1.000

分类结果分类结果2

3. 使用 scikit-learn训练逻辑回归模型

进一步使用scikit-learn训练逻辑回归模型，用于区分iris数据集的三个分类标签，该模型需有更高的预测精确度。

from sklearn.linear_model import LogisticRegression# LogisticRegression参数说明
# C=100.0：正则化强度的倒数，必须是一个正数。C被设置为100.0，这意味着正则化强度较弱，允许模型更复杂一些
# solver='lbfgs'：指定用于优化的算法，lbfgs是一种拟牛顿方法，适用于小数据集。其他常用的求解器包括liblinear（适用于二分类或多分类问题，具有L1或L2正则化）和saga（适用于L2正则化，且可以用于高维数据）
# multi_class='ovr'：指定如果目标变量具有多于两个类别时使用的算法。ovr代表“一对一”（One-vs-Rest），也称为多类别逻辑回归。在这种设置中，对于每个类别，模型会学习一个将其与其余类别区分开的二元分类器。# LogisticRegression类创建lr实例
lr = LogisticRegression(C=100.0, solver='lbfgs', multi_class='ovr')
lr.fit(X_train_std, y_train)# 绘图
plot_decision_regions(X_combined_std, y_combined,classifier=lr, test_idx=range(105, 150))plt.xlabel('Petal length [standardized]')
plt.ylabel('Petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()# 获取预测数据集中每个样本属于每个类别的概率
lr.predict_proba(X_test_std[:, :])
# array([[6.63770505e-09, 1.44747233e-01, 8.55252760e-01],
#       [8.34031210e-01, 1.65968790e-01, 3.20815954e-13],
#       [8.48822884e-01, 1.51177116e-01, 2.57998350e-14],# 使用argmax函数输出每个样本概率最高类别的索引
lr.predict_proba(X_test_std[:, :]).argmax(axis=1)
# array([2, 0, 0, 1, 1, 1, 2, 1, 2, 0, 0, 2, 0, 1, 0, 1, 2, 1, 1, 2, 2, 0,
#       1, 2, 1, 1, 1, 2, 0, 2, 0, 0, 1, 1, 2, 2, 0, 0, 0, 1, 2, 2, 1, 0,
#       0])# 输出测试数据集全部样本预测结果
lr.predict(X_test_std[:, :])

通过scikit-learn训练的回归模型，在预测标签1和2时，有少数样本分类错误，但预测精确度明显较高。
分类结果

4. 通过正则化处理过拟合

正则化 (regularization)：对模型复杂度的惩罚，正则化有助于防止模型出现过拟合。

欠拟合(underfitting): 欠拟合是指模型不能在训练集上获得足够低的误差。换句换说，就是模型复杂度低，模型在训练集上就表现很差，没法学习到数据背后的规律。

过拟合 (overfitting)：创建的模型与训练数据拟合程度过高，以致于模型无法根据未曾见过的新数据做出正确的预测。

欠拟合、拟合良好和过拟合示意图：
三种拟合情况
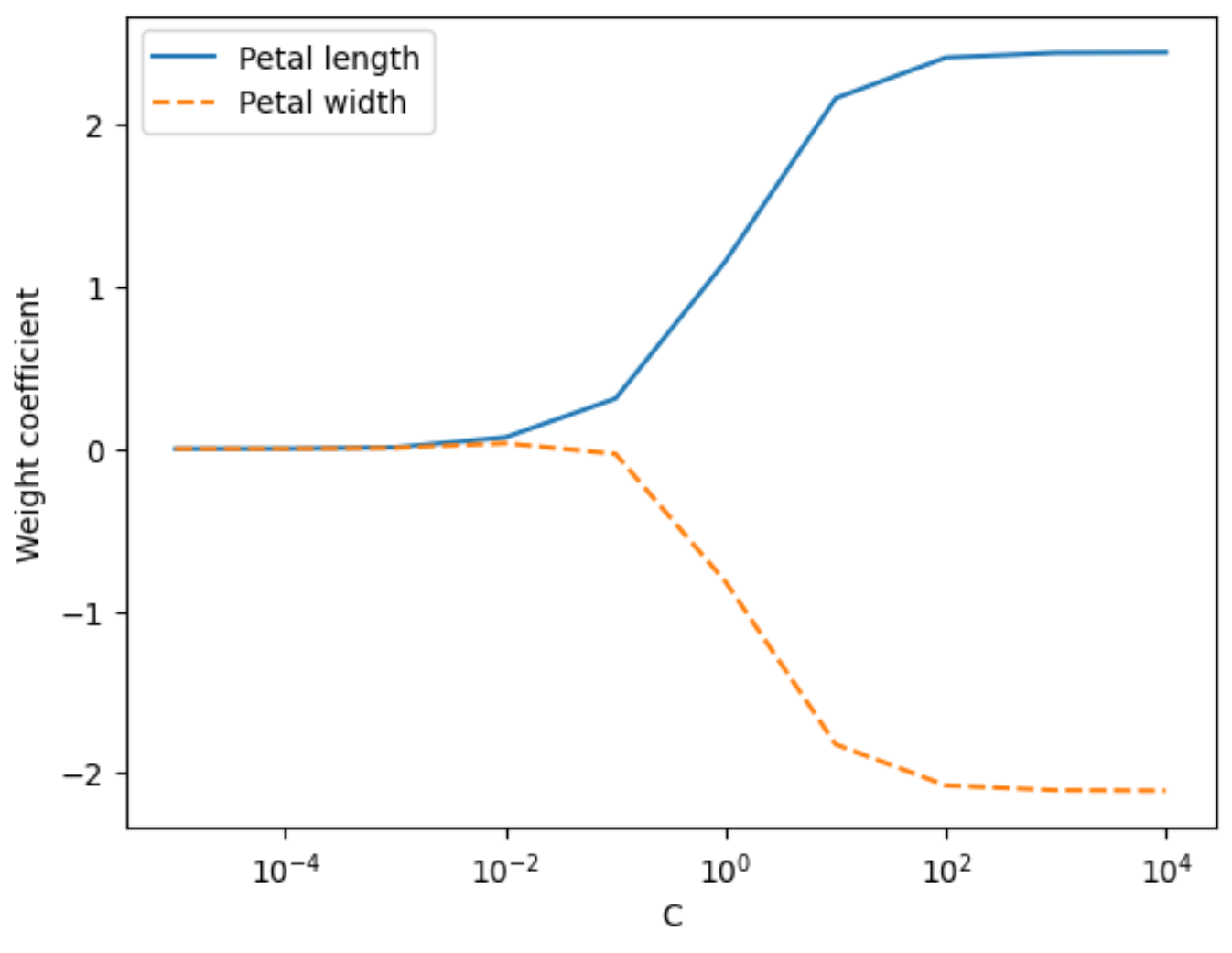
特征权重随C值变化图

# weights是用于存储权重系数的列表
# C是正则化项的倒数，用于控制正则化的强度，params是用于存储C值的列表
weights, params = [], []# 遍历数组-5到5之间数字（不包含5）
for c in np.arange(-5, 5):# C的值在每次迭代中以10的幂次方变化lr = LogisticRegression(C=10.**c,multi_class='ovr')# 使用标准化后的训练数据X_train_std和训练标签y_train来拟合模型lr.fit(X_train_std, y_train)#将模型的第二个类别的权重系数（lr.coef_[1]）添加到weights列表中weights.append(lr.coef_[1])params.append(10.**c)# 列表转numpy数组
weights = np.array(weights)# 绘制权重系数随C值变化的图
# weights[:, 0]和weights[:, 1]分别表示与花瓣长度和花瓣宽度相关的权重系数
plt.plot(params, weights[:, 0],label='Petal length')
plt.plot(params, weights[:, 1], linestyle='--',label='Petal width')plt.ylabel('Weight coefficient')
plt.xlabel('C')
plt.legend(loc='upper left')
plt.xscale('log')
plt.show()

权重系数随C值变化的图

5. 支持向量机实现分类模型

支持向量机（support vector machines，SVM）是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。由简单到复杂的模型包括：

当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机；
当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机；
当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机。

SVM分类原理图：

Scikit-learn 中的替代实现方法

from sklearn.linear_model import SGDClassifier# SGDClassifier类创建神经网络感知器实例
ppn = SGDClassifier(loss='perceptron')# SGDClassifier类创建逻辑回归分类器实例
lr = SGDClassifier(loss='log')# SGDClassifier类创建支持向量机分类器实例
svm = SGDClassifier(loss='hinge')

5.1 训练支持向量机分类模型

from sklearn.svm import SVC# kernel='linear' 作为核函数
# C=1.0 设置了正则化参数，它控制了误差项和模型复杂度之间的权衡
svm = SVC(kernel='linear', C=1.0, random_state=1)
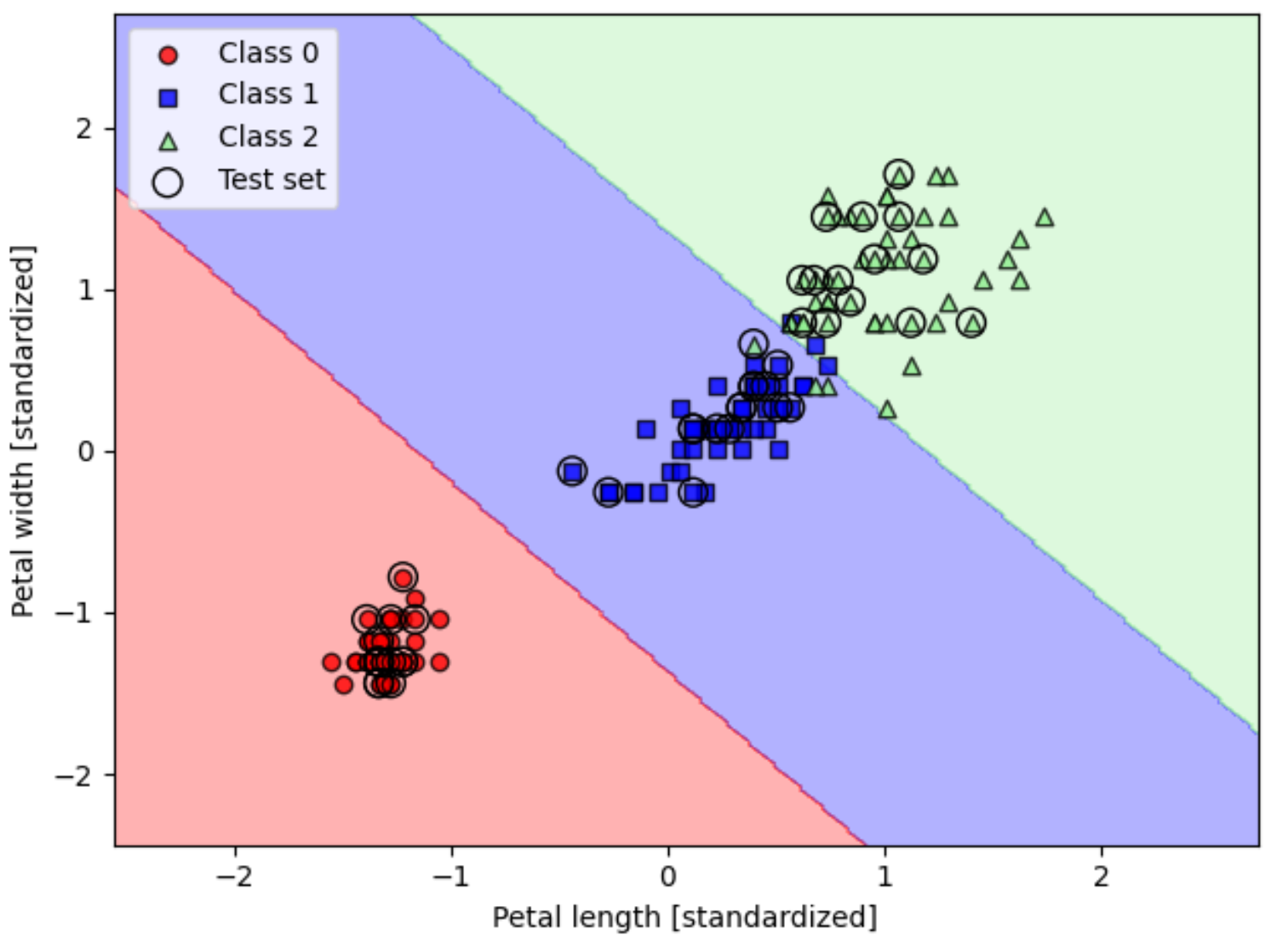
svm.fit(X_train_std, y_train)plot_decision_regions(X_combined_std, y_combined,classifier=svm, test_idx=range(105, 150))plt.xlabel('Petal length [standardized]')
plt.ylabel('Petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

分类结果

5.2 基于核支持向量机的非线性问题求解

import matplotlib.pyplot as plt
import numpy as np# numpy随机种子
np.random.seed(1)
# 生成一个形状为 (200, 2) 的数组，其中包含从标准正态分布（均值为0，标准差为1）中抽取的200个样本，每个样本有两个特征
X_xor = np.random.randn(200, 2)# 对每个样本，检查第一个特征是否大于0，然后检查第二个特征是否大于0。np.logical_xor 函数计算这两个条件的逻辑异或;
# 如果两个条件不同时为真（即一个为真，一个为假），则结果为 True，否则为 False。
y_xor = np.logical_xor(X_xor[:, 0] > 0,X_xor[:, 1] > 0)# 将逻辑值 True 和 False 转换为整数 1 和 0
y_xor = np.where(y_xor, 1, 0)# X_xor[y_xor == 1, 0] 选择了 y_xor = 1 的样本的第一个特征（即第一个维度）
# X_xor[y_xor == 1, 1] 选择了 y_xor = 1 的样本的第二个特征（即第二个维度）
plt.scatter(X_xor[y_xor == 1, 0],X_xor[y_xor == 1, 1],c='royalblue',marker='s',label='Class 1')# X_xor[y_xor == 0, 0] 选择了 y_xor = 0 的样本的第一个特征（即第一个维度）
# X_xor[y_xor == 0, 1] 选择了 y_xor = 0 的样本的第二个特征（即第二个维度）
plt.scatter(X_xor[y_xor == 0, 0],X_xor[y_xor == 0, 1],c='tomato',marker='o',label='Class 0')plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')plt.legend(loc='best')
plt.tight_layout()
plt.show()

SVM数据可视化 超平面(hpyerplane) 生成示意图：
SVM对数据集的操作

5.3 使用核方法（ kernel trick）获取高维空间中的分离超平面

# kernel='rbf' 指定了径向基函数（Radial Basis Function）作为核函数；RBF 核能够处理非线性问题，通过将数据映射到高维空间来找到合适的决策边界。
# random_state=1 设置随机数生成器的种子，确保结果的可复现性。
# gamma=0.10 设置了 RBF 核的参数，它定义了单个训练样本的影响范围。
# C=10.0 设置了正则化参数，它控制了误差项和模型复杂度之间的权衡。
svm = SVC(kernel='rbf', random_state=1, gamma=0.10, C=10.0)
svm.fit(X_xor, y_xor)# 绘制决策边界
plot_decision_regions(X_xor, y_xor,classifier=svm)plt.legend(loc='upper left')
plt.tight_layout()plt.show()

分类结果
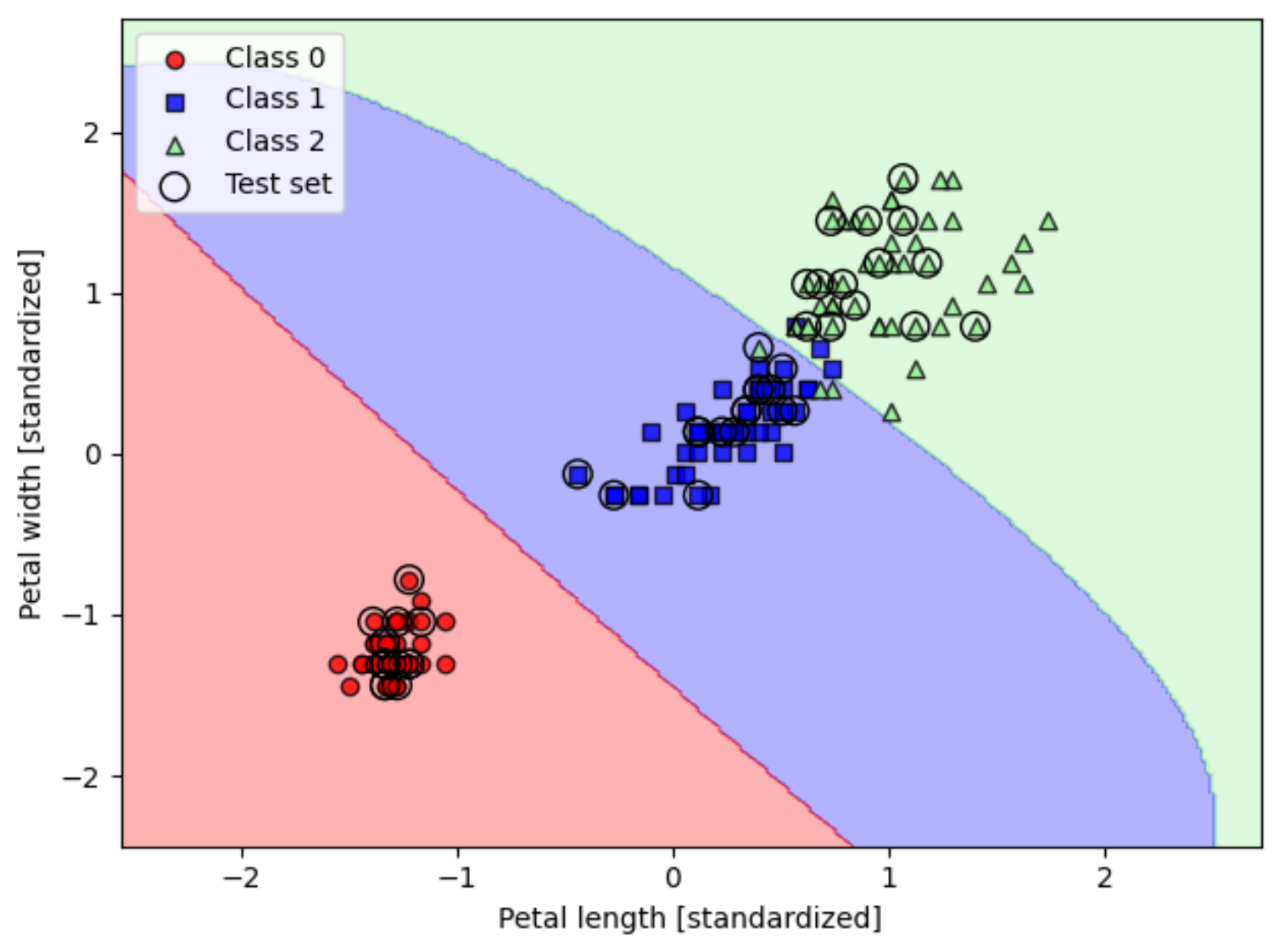
运用到全部标签的分类预测：

from sklearn.svm import SVC# 调整gamma=0.2和C=1
svm = SVC(kernel='rbf', random_state=1, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)# 绘图
plot_decision_regions(X_combined_std, y_combined,classifier=svm, test_idx=range(105, 150))plt.xlabel('Petal length [standardized]')
plt.ylabel('Petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

分类结果

# 调整gamma=100和C=1
svm = SVC(kernel='rbf', random_state=1, gamma=100.0, C=1.0)
svm.fit(X_train_std, y_train)plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150))plt.xlabel('Petal length [standardized]')
plt.ylabel('Petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()plt.show()