第一题 线性分类器

考虑一个简单的二分类问题——将二维平面上的点分为 $A$ 和 $B$ 两类。

训练数据包含 $n$ 个点，其中第 $i$ 个点（$1\le i\le n$）可以表示为一个三元组 $(x_i,y_i,typ{e}_i)$，即该点的横坐标、纵坐标和类别。

在二维平面上，任意一条直线可以表示为 ${\theta }_0+{\theta }_{1}x+{\theta }_{2}y=0$ 的形式，即由 ${\theta }_0、{\theta }_1$ 和 ${\theta }_2$ 三个参数确定该直线，且满足 ${\theta }_1、{\theta }_2$ 不同时为 $0$。

基于这 $n$ 个已知类别的点，我们想要在平面上找到一条直线作为一个线性分类器。

具体来说，这条线要把训练数据中的 $A、B$ 两类点完美分隔开来，即一侧只有 $A$ 类点、另一侧只有 $B$ 类点。

这样，对于任意一个的未知类别的点，我们就可以根据它是位于直线的哪一侧来预测它的类别了。

在本题中我们仅需要处理 $m$ 个如下查询：

给定一条直线，判断它是否能将训练数据中的 $A、B$ 两类点完美分开。

输入格式

输入共 $n+m+1$ 行。

第一行包含用空格分隔的两个正整数 $n$ 和 $m$，分别表示点和查询的个数。

第二行到第 $n+1$ 行依次输入 $n$ 个点的信息。第 $i+1$ 行（$1\le i\le n$）包含用空格分隔的三项 $x_i、y_i$ 和 $typ{e}_i$，分别表示第 $i$ 个点的横、纵坐标和类别，其中坐标为整数、类别为一个大写英文字母 $A$ 或 $B$。

第 $n+2$ 行到第 $n+m+1$ 行依次输入 $m$ 个查询。第 $j+n+1$ 行（$1\le j\le m$）包含用空格分隔的三个整数 ${\theta }_0、{\theta }_1$ 和 ${\theta }_2$，表示第 $j$ 个查询中给定直线的三个参数。

输出格式

输出共 $m$ 行，每行输出一个字符串。

第 $j$ 行（$1\le j\le m$）输出的字符串对应第 $j$ 个查询的结果：如果给定直线可以完美分隔 $A、B$ 两类点，则输出 Yes，否则输出 No。

数据范围

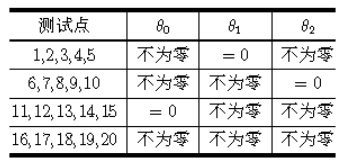
输入数据保证不存在恰好落在给定直线上的点;
$0<n\le 10^3、0<m\le 20$，且 $A、B$ 两类点的数量均不为 $0$;
所有点的坐标和给定直线的三个参数均为整数，且绝对值 $\le 10^6$;
任意两个点的坐标不完全相同。

输入样例：

9 3
1 1 A
1 0 A
1 -1 A
2 2 B
2 3 B
0 1 A
3 1 B
1 3 B
2 0 A
0 2 -3
-3 0 2
-3 1 1

输出样例：

No
No
Yes

样例解释

只有第 $3$ 个查询给出的直线能将 $A、B$ 两类点完美分隔。

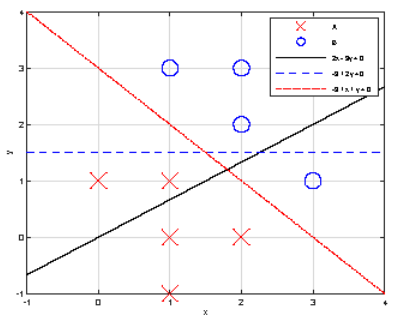
题目我的思路很简单，对于一个直线 L，一个点node, 考虑这个node在这个直线的相对位置，都在点的一侧的就是一类的点（就是把点延x,y轴向直线做投影，看投影的点与node的相对位置，判断左右和上下来区分，两侧的点的相对大小是不同的）

比如说一个点（x,y） , 和一条线（a + bx + cy = 0）那么有投影
（x , (a+bx)/-c） , ( (a+cy)/-b,y) 存在于线上 。 判断(a+bx)/-c 与 y 以及 (a+cy)/-b与x的大小就可以得到 点在线的上方还是下方，左边还是右边。（上图中（2，0）和（2，2）对于红线来说，（2，0）两个投影比较都为小于，而（2，2两个比较都为大于），则两个点应该不同类）
满分代码如下

#include<bits/stdc++.h>
using namespace std;
#define LL long long int main (){long long n,m;cin>>n>>m;LL h[n+1][2];char s[n+1];for(int i = 1 ; i <= n ; i++){cin>>h[i][0]>>h[i][1]>>s[i];}LL linear[m+1][3]; char c = s[1];for(int i = 1;i<= m ; i++){cin>>linear[i][0]>>linear[i][1]>>linear[i][2];LL temp[2]; bool flag = true;if(linear[i][2] == 0) {temp[1] = 0;}else{temp[1] = int(-1.0 * (linear[i][0] +linear[i][1] * h[1][0]) / linear[i][2] > h[1][1]) == 0 ? -1 : 1;}if(linear[i][1] == 0) {temp[0] = 0;}else{temp[0] = int(-1.0 * (linear[i][0] +linear[i][2] * h[1][1]) / linear[i][1] > h[1][0]) == 0 ? -1 : 1;}for(int j = 2 ; j<= n && flag ; j++){LL a = 0, b=0;if(linear[i][2] == 0) {b = 0;}else{b = int(-1.0 * (linear[i][0] +linear[i][1] * h[j][0]) / linear[i][2] > h[j][1]) == 0 ? -1 : 1;}if(linear[i][1] == 0) {a = 0;}else{a = int(-1.0 * (linear[i][0] +linear[i][2] * h[j][1]) / linear[i][1] > h[j][0]) == 0 ? -1 : 1;//cout<<-1.0 * (linear[i][0] +linear[i][2] * h[j][1]) / linear[i][1]<<'\n';}flag = ((((a==temp[0])+ (temp[1] == b)) == 2) ==(c==s[j]));//cout<<temp[0]<<temp[1]<<j<<a<<b<<' '<<c<<s[j]<<'\n'<<((a+b )== (temp[0] + temp[1]))<<' '<<(c==s[j])<<'\n';}if(flag) cout<<"Yes\n";else cout<<"No\n";}return 0;
}

我在做的时候犯了很多错：比如说忘了把1改为1.0 ,没有考虑到浮点数, 忘了加LL , 没有考虑到int爆炸，代码也写得很冗长。

第二题 稀疏向量

对于一个 $n$ 维整数向量 $v\in {\mathbb{Z}}^n$，其在第 $index$ 个维度上的取值记作 $v_{index}$。

这里我们约定 $index$ 的取值从 $1$ 开始，即 $v=(v_1,v_2,\dots ,v_n)$。

下面介绍一种向量的稀疏表示方法。

如果 $v$ 仅在少量维度上的取值不为 $0$，则称其为稀疏向量。

例如当 $n=10$ 时，$v=(0,0,0,5,0,0,-3,0,0,1)$ 就是一个稀疏向量。

由于稀疏向量的非零值较少，我们可以通过仅存储非零值的方式来节省空间。

具体来说，每个非零值都可以用一个 $(index,value)$ 对来表示，即该向量在第 $index$ 个维度上的取值 $v_{index}=value\ne 0$。

在上面的例子中，$v$ 就可以表示为 $[(4,5),(7,-3),(10,1)]$。

接下来给出这种稀疏表示一般化的定义。

• 对于任意一个 $n$ 维整数向量 $v\in {\mathbb{Z}}^n$，如果其在且仅在 $a$ 个维度上取值不为 $0$，则可以唯一表示为: $[(inde{x}_1,valu{e}_1),(inde{x}_2,valu{e}_2),\dots ,(inde{x}_a,valu{e}_a)]$。
• 其中所有的 $index$ 均为整数且满足: $1\le inde{x}_1<inde{x}_2<\dots <inde{x}_a\le n$。
• $valu{e}_i$ 表示向量 $v$ 在对应维度 $inde{x}_i$ 上的非零值。

给出两个 $n$ 维整数向量 $u,v\in {\mathbb{Z}}^n$ 的稀疏表示，试计算它们的内积。

$$u\cdot v=\sum _{i=1}^n{u}_i\cdot v_i$$

输入格式

第一行包含用空格分隔的三个正整数 $n、a$ 和 $b$，其中 $n$ 表示向量 $u、v$ 的维数，$a$ 和 $b$ 分别表示两个向量所含非零值的个数。

第二行到第 $a+1$ 行输入向量 $u$ 的稀疏表示。第 $i+1$ 行（$1\le i\le a$）包含用空格分隔的两个整数 $inde{x}_i$ 和 $valu{e}_i$ 表示 $v_{inde{x}_i}=valu{e}_i\ne 0$。

第 $a+2$ 行到第 $a+b+1$ 行输入向量 $v$ 的稀疏表示。第 $j+a+1$ 行（$1\le j\le b$）包含用空格分隔的两个整数 $inde{x}_j$ 和 $valu{e}_j$ 表示 $v_{inde{x}_j}=valu{e}_j\ne 0$。

输出格式

输出一个整数，表示向量 $u$ 和 $v$ 的内积 $u\cdot v$。

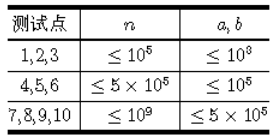
数据范围

输入数据保证 $0<a,b<n$;
向量 $u$ 和 $v$ 在每一维度上取值的绝对值 $|u_i|,|v_i|\le 10^6(1\le i\le n)$。

输入样例：

10 3 4
4 5
7 -3
10 1
1 10
4 20
5 30
7 40

输出样例：

-20

样例解释

$u=(0,0,0,5,0,0,-3,0,0,1)$
$v=(10,0,0,20,30,0,40,0,0,0)$
$u\cdot v=5\times 20+(-3)\times 40=-20$

题目的思路也很简单，用两个列表存一下，然后双指针遍历一次就行了。
满分代码如下：

#include<bits/stdc++.h>
using namespace std;
#define LL long long int main (){int n,a,b;cin>>n>>a>>b;LL h[a+1][2] , s[b+1][2];for(int i=1;i<=a;i++){cin>>h[i][0]>>h[i][1];}for(int i=1;i<=b;i++){cin>>s[i][0]>>s[i][1];}int l=1,r=1;LL sum = 0;while(l<=a && r <= b){if(h[l][0]<s[r][0]) {l++;continue;}if(h[l][0]>s[r][0]) {r++;continue;}if(h[l][0] == s[r][0]){sum += h[l++][1] * s[r++][1];}}cout<<sum;return 0;
}

在上一个题目后我已经一来就开LL了,但是。。。。。我只是给sum开了一个LL，没有考虑到两个int数组的数相乘也会爆int。。。

未完待续。。。