用Matlab求解绘制2D散点（x y）数据的最小外接矩形

0 引言
1 原理介绍及实现
2 完整代码及相关函数
3 结语

0 引言

散点/多边形的外接图形是确定模型轮廓或姿态的一种可视化方法，也是有很大的用途的。前面已经介绍过两种简单的散点 ${(x,y)}$ 外接图形的原理及实现过程，本篇继续理解下散点数据最小外接矩形的原理。

😜 且听絮叨

前面提到的沿轴外接矩形，实际是一种简单的外接矩形，因为沿轴，所以方向已知，在 $XO Y$ 面内只有一个解，所以比较好求；最小外接矩形通常指面积最小或周长最小，在随机点中找满足条件的矩形，就需要在 $XO Y$ 内旋转矩形使其可以包含所有随机点，且面积/周长最小的，即为符合要求的解。本篇基于网上资料使用凸包算法求解散点的最小外接矩形。

1 原理介绍及实现

先介绍下凸包算法求解最小外接矩形的步骤：

（1）先找散点 ${(x_{i},y_{i})}$ 的凸包点或最小外包多边形，问题转化为了求多边形的最小外接矩形。找凸包点可以调用matlab函数convhull，返回凸包点的坐标索引，进而可以得到外接多边形的角点坐标；

edges = convhull(x,y); 
plot(x(edges),y(edges),'Color','b')

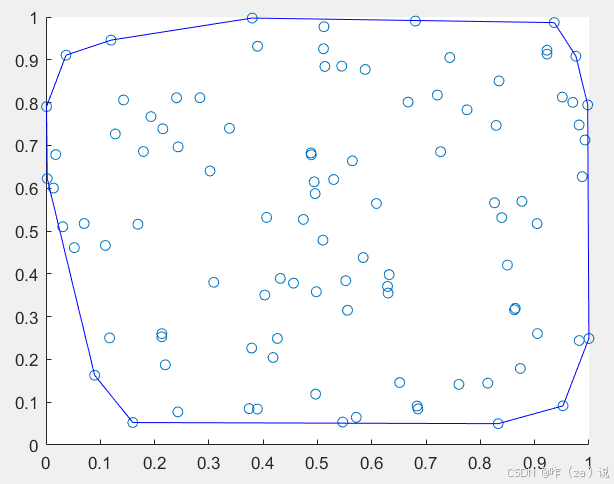
（2）以 $n$ 边形的一条边 $(A - B)$ 为例，假设矩形的某边平行于 $(A - B)$ ，那么通过 $(A - B)$ 仅有一个矩形可以包含所有散点。所以一共可以找到 $n$ 个矩形，通过比较n个矩形，找到满足面积最小/周长最小的一个即为所求解。

（3）如何找到平行于 $(A - B)$ 边的矩形呢？ 假设 $(A - B)$ 边平行于Y轴，那么问题就等价于前面介绍过的找沿轴外接矩形的过程；若 $(A - B)$ 边不平行于Y轴，只用将所有散点或角点坐标旋转到以 $(A - B)$ 为轴的坐标系下，然后用找沿轴外接矩形的原理，就能找到一个以 $(A - B)$ 为边的矩形。

下面为示例代码，相关函数在下一部分。

%% 散点外接图形
clc;clear;
n = 100;
x = rand(n,1); % 随机数
y = rand(n,1);figure(1)
scatter(x,y,'o')
hold on% 凸包多边形
edges = convhull(x,y); 
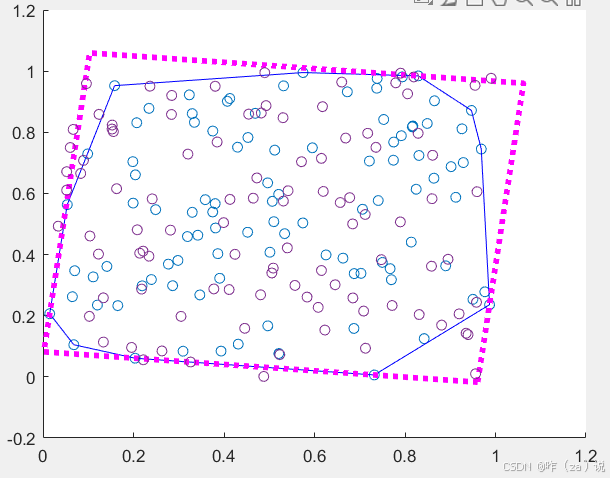
plot(x(edges),y(edges),'Color','b')% 散点x y最小外接矩形(XX最小)
[rectx,recty,area,perimeter] = minboundrect(x,y,'p');
hold on
plot(rectx,recty,Color='c',LineStyle='--',LineWidth=3.4);

2 完整代码及相关函数

💦💦💦💦💦

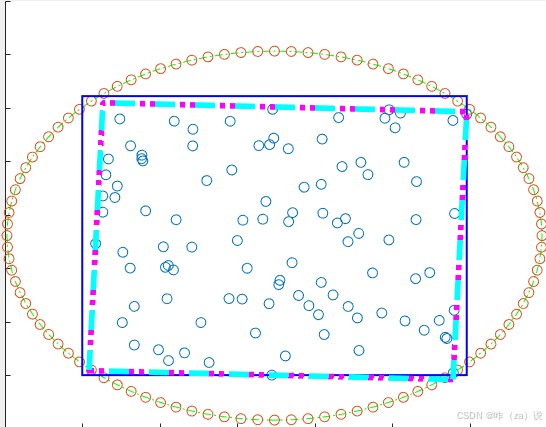
%% 散点求外接图形，与前面提到的两种进行对比
clc;clear;
n = 100;
x = rand(n,1); % 随机数
y = rand(n,1);figure(1)
scatter(x,y,'o')
hold on% 绘制外接圆(方法1)
[center_x,center_y,r] = maxBoundCycle(x,y);
para = [center_x-r, center_y-r, 2*r, 2*r];
rectangle('Position', para, 'Curvature', [1 1],'EdgeColor','g',LineStyle='-.');% 绘制外接圆(方法2)
hold on
theta = 0:pi/50:2*pi; %角度[0,2*pi] 
xx = center_x + r*cos(theta);
yy = center_y + r*sin(theta);
plot(xx,yy,'o')% 散点x y外接矩形[沿轴]
hold on
[boundary] = maxBoundRect(x,y);
plot(boundary(:,1),boundary(:,2),Color='b',LineStyle='-',LineWidth=1.2);% 散点x y最小外接矩形[√]
[rectx,recty,area,perimeter] = minboundrect(x,y,'a');
hold on
plot(rectx,recty,Color='m',LineStyle=":",LineWidth=3.4);

% 最小外接矩形(求解函数)
function [rectx,recty,area,perimeter] = minboundrect(x,y,metric)
% minboundrect: Compute the minimal bounding rectangle of points in the plane
% usage: [rectx,recty,area,perimeter] = minboundrect(x,y,metric)
%
% arguments: (input)
%  x,y - vectors of points, describing points in the plane as
%        (x,y) pairs. x and y must be the same lengths.
%
%  metric - (OPTIONAL) - single letter character flag which
%        denotes the use of minimal area or perimeter as the
%        metric to be minimized. metric may be either 'a' or 'p',
%        capitalization is ignored. Any other contraction of 'area'
%        or 'perimeter' is also accepted.
%
%        DEFAULT: 'a'    ('area')
%
% arguments: (output)
%  rectx,recty - 5x1 vectors of points that define the minimal
%        bounding rectangle.
%
%  area - (scalar) area of the minimal rect itself.
%
%  perimeter - (scalar) perimeter of the minimal rect as found
%
%
% Note: For those individuals who would prefer the rect with minimum
% perimeter or area, careful testing convinces me that the minimum area
% rect was generally also the minimum perimeter rect on most problems
% (with one class of exceptions). This same testing appeared to verify my
% assumption that the minimum area rect must always contain at least
% one edge of the convex hull. The exception I refer to above is for
% problems when the convex hull is composed of only a few points,
% most likely exactly 3. Here one may see differences between the
% two metrics. My thanks to Roger Stafford for pointing out this
% class of counter-examples.
%
% Thanks are also due to Roger for pointing out a proof that the
% bounding rect must always contain an edge of the convex hull, in
% both the minimal perimeter and area cases.
%
%
% See also: minboundcircle, minboundtri, minboundsphere
%
%
% default for metric
if (nargin<3) || isempty(metric)metric = 'a';
elseif ~ischar(metric)error 'metric must be a character flag if it is supplied.'
else% check for 'a' or 'p'metric = lower(metric(:)');                    ind = strmatch(metric,{'area','perimeter'});             if isempty(ind)                error 'metric does not match either ''area'' or ''perimeter'''end% just keep the first letter.metric = metric(1);
end% preprocess data
x=x(:);
y=y(:);% not many error checks to worry about
n = length(x);                                    
if n~=length(y)                               error 'x and y must be the same sizes'
end% start out with the convex hull of the points to
% reduce the problem dramatically. Note that any
% points in the interior of the convex hull are
% never needed, so we drop them.
if n>3edges = convhull(x,y);  % 'Pp' will silence the warnings% exclude those points inside the hull as not relevant% also sorts the points into their convex hull as a% closed polygonx = x(edges);y = y(edges);% probably fewer points now, unless the points are fully convexnedges = length(x) - 1;                       
elseif n>1% n must be 2 or 3nedges = n;x(end+1) = x(1);y(end+1) = y(1);
else% n must be 0 or 1nedges = n;
end% now we must find the bounding rectangle of those
% that remain.% special case small numbers of points. If we trip any
% of these cases, then we are done, so return.
switch nedgescase 0% empty begets emptyrectx = [];recty = [];area = [];perimeter = [];returncase 1% with one point, the rect is simple.rectx = repmat(x,1,5);recty = repmat(y,1,5);area = 0;perimeter = 0;returncase 2% only two points. also simple.rectx = x([1 2 2 1 1]);recty = y([1 2 2 1 1]);area = 0;perimeter = 2*sqrt(diff(x).^2 + diff(y).^2);return
end
% 3 or more points.% will need a 2x2 rotation matrix through an angle theta
Rmat = @(theta) [cos(theta) sin(theta);-sin(theta) cos(theta)];% get the angle of each edge of the hull polygon.
ind = 1:(length(x)-1);
edgeangles = atan2(y(ind+1) - y(ind),x(ind+1) - x(ind));
% move the angle into the first quadrant.
edgeangles = unique(mod(edgeangles,pi/2));% now just check each edge of the hull
nang = length(edgeangles);              
area = inf;                           
perimeter = inf;
met = inf;
xy = [x,y];
for i = 1:nang                         % rotate the data through -theta rot = Rmat(-edgeangles(i));xyr = xy*rot;xymin = min(xyr,[],1);xymax = max(xyr,[],1);% The area is simple, as is the perimeterA_i = prod(xymax - xymin);P_i = 2*sum(xymax-xymin);if metric=='a'M_i = A_i;elseM_i = P_i;end% new metric value for the current interval. Is it better?if M_i<met% keep this onemet = M_i;area = A_i;perimeter = P_i;rect = [xymin;[xymax(1),xymin(2)];xymax;[xymin(1),xymax(2)];xymin];rect = rect*rot';rectx = rect(:,1);recty = rect(:,2);end
end