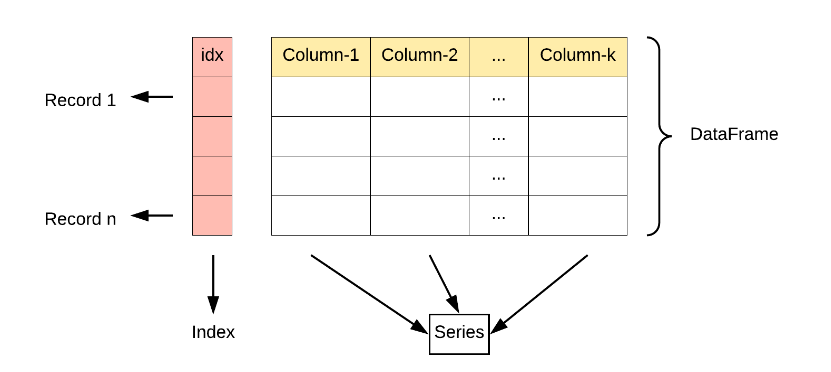
- 标准库中的string类没有实现像C#和Java中string类的split函数,所以想要分割字符串的时候需要我们自己手动实现。但是有了
stringstream类就可以很容易的实现,stringstream默认遇到空格、tab、回车换行会停止字节流输出。
#include <sstream>
#include <iostream>int main()
{std::stringstream ss("this apple is sweet");std::string word;while (ss >> word){std::cout << word << std::endl; // 这里依次输出this、apple、is、sweet四个单词}return 0;
}
- 可以使用
getline()函数用其他字符分割字符串,第一个参数 - 流中获取数据,第二个参数 - 把数据转换成字符串,第三个参数 - 分隔符。
#include <sstream>
#include <iostream>int main()
{std::string str = "this,is,apple";std::istringstream ss(str);std::string token;while (std::getline(ss, token, ',')) {std::cout << token << '\n'; // 这里依次输出this、is、apple三个单词}return 0;
}
- 匿名函数实现一个功能,输入一个由空格分割单词的字符串,就计算出每个单词的出现频率:
unordered_map<string, int> freq;auto insert = [&](string s) {stringstream ss(s);string word;while (ss >> word) {++freq[move(word)];}};insert(s1);
accumulate是numeric库中的一个函数,主要用来对指定范围内元素求和,但也自行指定一些其他操作,如范围内所有元素相乘、相除等。
int main() {vector<int> arr{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};int sum = accumulate(arr.begin(), arr.end(), 0); // 初值0 + (1 + 2 + 3 + 4 +... + 10)int sum = accumulate(arr.begin(), arr.end(), 1, multiplies<int>()); // 初值1 * (1 * 2 * 3 * 4 *... * 10)cout << sum << endl; return 0;
}
- 计算gcd 最大公约数的算法
int gcd(int a, int b){return b ? gcd(b, a % b) : a;
},
- C++取均匀随机数的方法
mt19937 gen{random_device{}()};//声明:产生器+种子。
//--上面这俩需要#include<random>
//由于gen的初始化里面也是一个发生器,因此要{}
// random_device先加{}产生一个随机产生器对象,再()产生种子
uniform_int_distribution<int> dis(1,5);//声明:取数器
int ans = dis(gen);//ans是1~5中均匀概论取到的。
- 对一个数组中每个元素进行第三项中函数的判断
return all_of(arr.begin(), arr.end(), [n](int x){ return x %n == 0; });
- 位运算中 x&(x-1) 相当于把 x 的最后一位1去掉:
// 衍生题:统计一个数二进制表示中1的个数
int func(x)
{ int countx = 0; while(x) { countx ++; x = x&(x-1); } return countx;
}
如果 n是正整数并且 n & (n - 1) = 0,那么 n 就是 2的幂;如果 n是正整数并且 n & (-n) = n,那么 n就是 2的幂。
令 y=x & (x−1),则 y 为 将x的最末位的1改成0的数字。
x除以2 可以通过x>> 1(x右移一位得到),x除以2的余数可以通过 x& 1得到
x&(-x)的用途:
1.可用于获取某个二进制数的最低位1所对应的值
2.求一个偶数能被整除的最大的二次幂

lower_bound( )和upper_bound( )都是利用二分查找的方法在一个排好序的数组中进行查找的。
在从小到大的排序数组中,
lower_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字,找到返回该数字的地址,不存在则返回.end()。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
upper_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于num的数字,找到返回该数字的地址,不存在则返回.end()。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
- 优先队列-小顶堆
/*优先队列-小顶堆*/static bool cmp(pair<int,int> &m,pair<int,int> &n){return m.second>n.second;}//C++11新标准引入了decltype类型说明符,它的作用是选择并返回操作数的数据类型
//在此过程中,编译器分析表达式并得到它的类型,却不实际计算表达式的值。
// 升序队列,先弹小的元素出来:priority_queue
priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(&cmp)> q(cmp);
> 基本数据类型的优先级设置:(即可以直接使用的数据类型),优先队列对他们的优先级设置一般是数字越大的优先级越高,因此队首是优先级最大的那个(如果是 char 类型,则是字典序最大的)。以 int 型为例下面两种是等价的:
> > priority_queue<int>q;
> > priority_queue<int,vector<int>,less<int> >q;
> > 可以发现第二种定义方式的尖括号内多出了两个参数:其中 vector<int>填写的是承载底层数据结构堆 (heap)的容器,如果是其他类型 可写为 vector<char>或vector<char>;
>
>
> //构造一个空的优先队列,此优先队列是一个小顶堆
>
> priority_queue<int,vector<int>,greater<int> > small_heap;
> > 第三个参数 less<int> 则是对第一个参数的比较类,!!less<int> 表示数字大的优先级越大,而 greater<int> 表示数字小的优先级越大。
>
“ ^ ”的异或指的是二进制中,对应的对应二进制位相同时异或为零,相异时异或为一1、任何数和 0 做异或运算,结果仍然是原来的数,即 a⊕0=a
2、任何数和其自身做异或运算,结果是 0,即 a⊕a=0
3、异或运算满足交换律和结合律,即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b
4、x=ai⊕aj 等价于 aj=x⊕ai// 通过异或来判断两个数的正负
if (numeratorLong < 0 ^ denominatorLong < 0) {sb.append('-');}
- 关于 substr:
//如果我要取索引i到索引j这一段子串,就使用:
substr(i,j-i+1)
// 数字转字符串
string str = to_string( int value );
to_string( float value );
to_string( long value );// 数字转字符
s[i]+'0';// 字符转数字
s[i]-'0';// 数字字符串转成数字
char a[]="-100"; char b[]="123"; int c;
c=atoi(a.c_str())+atoi(b.c_str());
printf("c=%d\n",c); //c = 23//判断一个字符是否为字母或者数字:
//字母(不区分大小写):
isalpha();
// 数字
isdigit();
//字母和数字
isalnum();// 字符串转数字:stoi(字符串,起始位置,n进制),将 n 进制的字符串转化为十进制
string s = "12345";
int num1 = stoi(s);
- 利用快慢指针来找到链表的中间节点
ListNode* getMidNode (ListNode* head){ListNode* fast = head;ListNode* slow = head;while(fast->next != nullptr && fast->next->next != nullptr){fast = fast->next->next;slow = slow->next;}return slow;}
- 在 C++ 中,可以使用
std::map来实现键值对的有序存储,但是std::map默认是按照键(key)的升序进行排序的。希望按照值(value)进行排序,然后在值相同时再按照键进行排序,需要借助一个辅助数据结构来实现。一种常用的方法是使用std::vector来存储std::map中的键值对,然后对 std::vector 进行排序,并且自定义排序规则。
#include <iostream>
#include <map>
#include <vector>
#include <algorithm>int main() {using namespace std; // 引入命名空间,可以省略 std::// 定义一个 map,假设键为字符串,值为整数map<string, int> myMap = {{"apple", 3},{"orange", 2},{"banana", 1},{"grape", 2}};// 定义一个 vector 来存储 map 中的键值对vector<pair<string, int>> vec(myMap.begin(), myMap.end());// 使用 Lambda 表达式定义排序规则sort(vec.begin(), vec.end(), [](const pair<string, int>& a, const pair<string, int>& b) {if (a.second == b.second) { // 如果值相同,按照键进行升序排序return a.first < b.first;}return a.second < b.second; // 否则按照值进行升序排序});// 打印排序后的结果for (const auto& pair : vec) {cout << pair.first << ": " << pair.second << endl;}return 0;
}
- 如果我想在unordered_set中存储整数对时,可以使用自定义哈希函数:
using PII = pair<int,int>;auto hash_function = [](const PII& o){return hash<int>()(o.first) ^ hash<int>()(o.second);};unordered_set<PII,decltype(hash_function)> seen(0,hash_function);
- 裴蜀定理(或贝祖定理)得名于法国数学家艾蒂安·裴蜀,说明了对任何整数a、b和它们的最大公约数d,关于未知数x和y的线性不定方程(称为裴蜀等式):若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。
它的一个重要推论是:a,b互质的充分必要条件是存在整数x,y使ax+by=1.
- lamda函数+优先队列的写法:
auto cmp = [&nums1,&nums2](const pair<int,int> &a,const pair<int,int> &b){return nums1[a.first]+nums2[a.second]> nums1[b.first]+nums2[b.second];};priority_queue<pair<int,int>, vector<pair<int,int>>, decltype(cmp)> pq(cmp);
- 发现的一个小规律:
在一个环内,如果设置快慢指针,如果 fast 比 slow 的起始位置 前一个,此后 slow走一步,fast走2步,二者最终会在 起始点的 前一个位置(也就是走入下一次环的最后位置) 重合。
(1+2n) % x = n % x , n = x-1时 等式成立
- Dilworth定理
对于任意有限偏序集,其最大反链中元素的数目必等于最小链划分中链的数目。此定理的对偶形式亦真。
二 偏序集中的概念
链 : D 中的一个子集 C 满足 C 是全序集 及C中所有元素都可以比较大小
反链 : D 中的一个子集 B 满足 B 中任意非空子集都不是全序集 即所有元素之间都不可以比较大小
链覆盖 : 若干个链的并集为 D ,且两两之间交集为 ∅
反链覆盖 : 若干个反链的并集为 D ,且两两之间交集为∅
最长链 : 所有链中元素个数最多的 (可以有多个最长链)
最长反链 : 所有反链中元素个数最多的 (可以有多个最长反链
偏序集高度 : 最长链的元素个数
偏序集宽度 : 最长反链中的元素个数
最小链覆盖(使链最少)= 最长反链长度 = 偏序集宽度
最小反链覆盖=最长链长度=偏序集深度
该定理可以应用在拦截导弹的题目中,题目问这个序列最少可以划分为多少个非递增序列,根据Dilworth定理,我们只需求最长上升子序列的长度就是答案













![[项目实战]EOS多节点部署](https://i-blog.csdnimg.cn/direct/8301f61788f54ca68908e2a3c712ea05.png)