题目描述
质数是在数论中很有意思的数,有很多题都可以围绕它来出,就如你眼前所见的这道题。
给定一个闭区间 [a,b] ,将此范围内的所有素数进行从小到大排序,对于连续的素数,我们可以发现很多等差数列(元素个数大于等于 3 ),现在就请你完成这个任务。
对于给定的闭区间 [a,b] ,你要找出里面所有的等差数列,并输出所有的等差数列。
这里有一个要求,同一个数不能同时存在于两个等差数列中。
比如 a,b,c,d,e 中, a,b,c 是一个等差数列, c,d,e 也是一个等差数列,后一个等差数列就不能以 c 开始,所以 c,d,e 在本题不构成等差数列。
输入格式
输入占一行,只包含两个数 a 和 b ,并用空格隔开。
输出格式
输出占若干行,每行为一个等差数列,每个数用空格隔开。
样例输入输出
样例输入
141 400
样例输出
151 157 163
167 173 179
199 211 223
251 257 263 269
367 373 379
数据范围
对于 100% 的数据,保证 a<b,a≤1000,b≤100000 。
来源/分类(难度系数:三星)
质数 模拟 NOIP普及组
完整代码展示:
def prime(i):
j=2
k=int(pow(i,0.5))
while j<=k:
if i%j==0:
break
j+=1
if j>k:
return 1
else:
return 0
def AP(j):
s=[]
m=max(j)
n=min(j)
l=int((m-n)/(len(j)-1))
for i in range(0,len(j)):
s.append(n+i*l)
if s==j:
return 1
else:
return 0
x=[]
a,b=map(int,input().split())
for i in range(a,b+1):
if prime(i)==1 and i>=2:
x.append(i)
y=[]
for i in range(0,len(x)-3):
for j in range(i+3,len(x)):
z=x[i:j]
if len(y)==0:
if AP(z)==1:
y.append(z)
else:
if AP(z)==1 and y[-1][0]==z[0] and len(z)>len(y[-1]):
y[-1]=z
elif AP(z)==1 and min(z)>max(y[-1):
y.append(z)
for i in range(0,len(y)):
sum=""
for j in range(0,len(y[i])):
sum+="{} ".format(y[i][j])
print(sum)
def prime(i):j=2k=int(pow(i,0.5))while j<=k:if i%j==0:breakj+=1if j>k:return 1else:return 0
def AP(j):s=[]m=max(j)n=min(j)l=int((m-n)/(len(j)-1))for i in range(0,len(j)):s.append(n+i*l)if s==j:return 1else:return 0
x=[]
a,b=map(int,input().split())
for i in range(a,b+1):if prime(i)==1 and i>=2:x.append(i)
y=[]
for i in range(0,len(x)-3):for j in range(i+3,len(x)):#将i+3错误写为3,导致出现:ZeroDivisionErrorz=x[i:j]if len(y)==0:if AP(z)==1:y.append(z)else:if AP(z)==1 and y[-1][0]==z[0] and len(z)>len(y[-1]):#尽可能地延长等差数列y[-1]=zelif AP(z)==1 and min(z)>max(y[-1]):#保证数列符合所给条件y.append(z)
for i in range(0,len(y)):sum=""for j in range(0,len(y[i])):sum+="{} ".format(y[i][j])print(sum)
代码解释:
“def prime(i):
j=2
k=int(pow(i,0.5))
while j<=k:
if i%j==0:
break
j+=1
if j>k:
return 1
else:
return 0 ”,根据素数的定义自定义一个函数prime(),用于判断prime()函数中实参是否为素数:如果是,则返回值1,否则返回值0。
“def AP(j):
s=[]
m=max(j)
n=min(j)
l=int((m-n)/(len(j)-1))
for i in range(0,len(j)):
s.append(n+i*l)
if s==j:
return 1
else:
return 0 ”,根据等差数列的定义自定义一个函数AP(),用于判断AP()中的实参是否为等差数列,如果是:则返回值1,否则返回值0。
“x=[]
a,b=map(int,input().split())
for i in range(a,b+1):
if prime(i)==1 and i>=2:
x.append(i) ”,建立一个空列表x,接着导入用户给定的闭区间[a,b]。遍历a~b的所有数字,将属于素数的数字添加进列表x中。
“y=[]
for i in range(0,len(x)-3):
for j in range(i+3,len(x)):
z=x[i:j]
if len(y)==0:
if AP(z)==1:
y.append(z)
else:
if AP(z)==1 and y[-1][0]==z[0] and len(z)>len(y[-1]):
y[-1]=z
elif AP(z)==1 and min(z)>max(y[-1]):#保证数列符合所给条件
y.append(z) ”,建立一个空列表y,接着遍历x中元素,按顺序截取元素个数大于等于三的数列。如果y列表为空,则将第一个符合等差数列的数列添加进y中;否则1:判断新查找得到的等差数列与y中的最后一个数列y[-1]是否有重复元素,如果没有,则将其添加进y中。2:判断新查找得到的等差数列的第一个元素与y中最后一个元素y[-1]的第一个元素相同且该数列的长度大于y[-1],如果是,则将该数列替换y[-1]。
“for i in range(0,len(y)):
sum=""
for j in range(0,len(y[i])):
sum+="{} ".format(y[i][j])
print(sum) ”,遍历y中元素:建立一个空字符串sum,sum依次连接y[i]中的元素,最终打印sum。
运行效果展示:
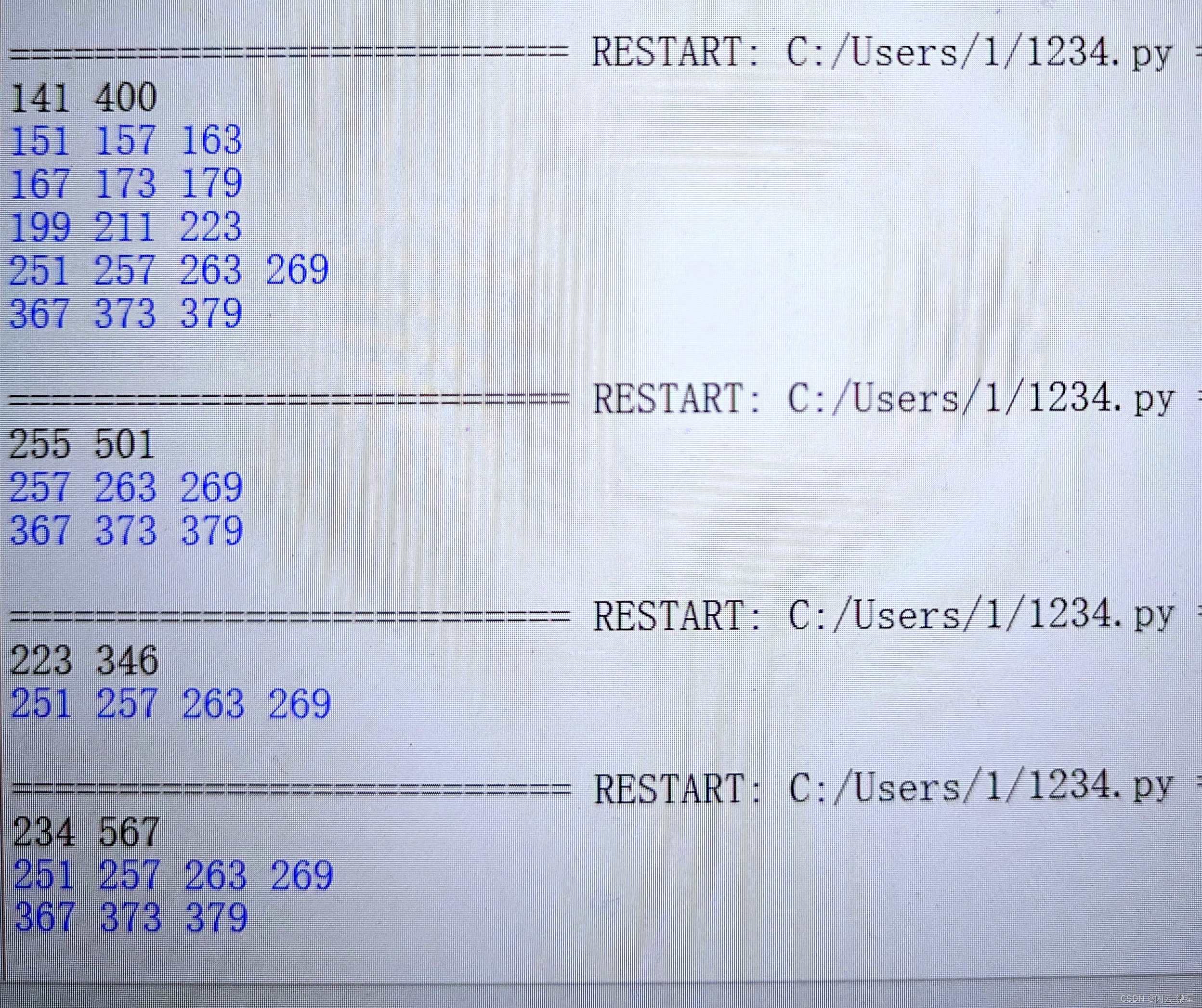
(声明:以上内容均为原创)