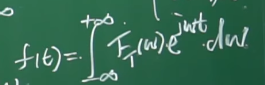一)  傅里叶分解

    任何一个时域空间的周期性函数都可以分解成一组正(余)弦波,

(图一)

二)  傅里叶变换

时域函数 -> 频域函数

f(t)  经过F操作分解成一组正余弦波(F操作为傅里叶变换)

 (图二)

怎么在频域空间描述这组正余弦波呢,直觉的答案是用不同频率和相应的振幅来描述(比如3w频率波的振幅大约是w频率波振幅的一半),

可是要做到从时域空间到频域空间完美的一一映射,光记录频率对应的振幅是不够的,还要记录频率的相位,

这样就实现从时域空间到频域空间的一一映射了.(如图二)

用数学公式表示分解后的正余弦波,实际上是一组标准正交基{1, sin(nwt) , cos(nwt)}的线性组合

根据欧拉公式,标准正交基变成了 或 

知道傅里叶变换后的一组正余弦波的数学形式和标准正交基实际上为 了,该怎么把这正余弦波具体求出来呢?

答案是根据标准正交基的性质,同频率的正交基相乘保留,不同频率的正交基相乘为0.

(图三)

图三里面的w代表某一特定频率值,这个对整个域的积分实际上就把频率为w的分量保留(提取)出来了,其他频率的分量被剔除掉了.

图三的积分就是傅里叶变换F了,从含有就可以看出傅里叶变换后的结果是个复数,

(图四)

这个复数里面的实部代表w波的振幅,虚部代表w波的相位.

由于从时域到频域的傅里叶变换是一一映射,所以存在一个傅里叶逆变换,使得变换之后信号(波)可以回答原始信号(波).

傅里叶逆变换公式如下