【Leetcode】70. 爬楼梯

题目来源

70. 爬楼梯

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶
2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶

提示：

1 <= n <= 45

知识点：动态规划、数学

题目解析

问题分析

题目是一道经典的爬楼梯问题，每次你可以爬1或2个台阶，问有多少种不同的方法可以爬到楼顶。

以下分析以10个阶梯距离

问题一：当我们从最后来看，如果只差最后一步就可以走到第10个阶梯，有几种情况？

情况一：剩一个阶梯，从9到10

情况二，剩两个阶梯，从8到10

也就是说，要想到达最后一个阶梯，最后一步要么是还剩一个阶梯，要么还剩两个阶梯

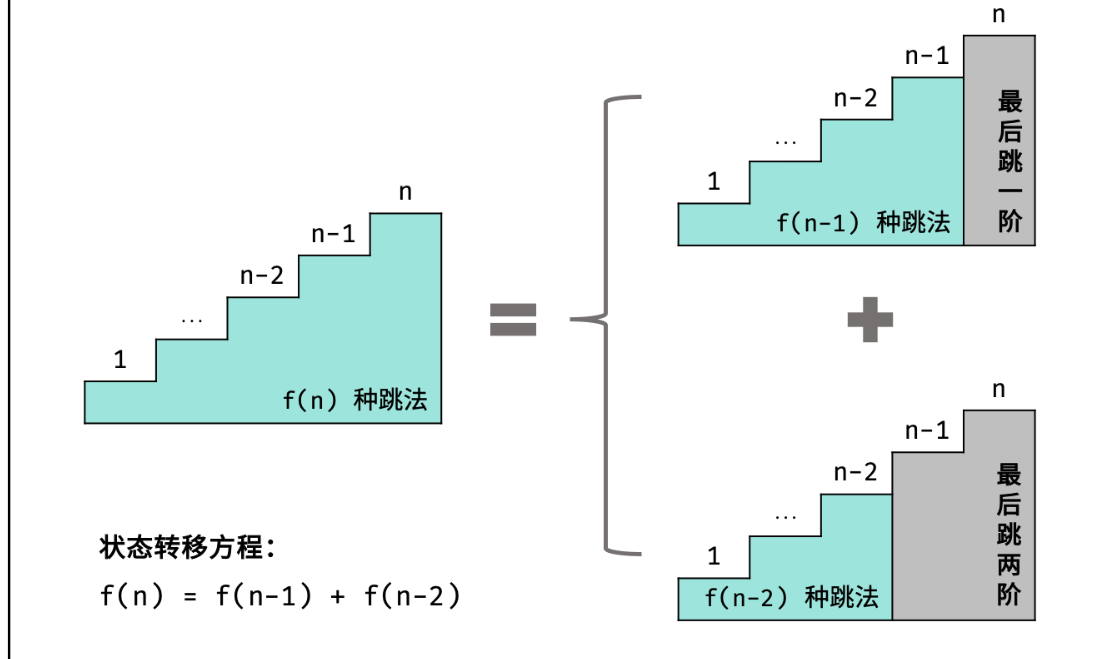
总结：

那么对于动态规划类型，首先我们就需要转换视角，先从最后来看

问题二：假设到达第8层的走法有F（8）种，到达第9层的有F（9）种，那么到达第10层的走法有多少种？

那么基于问题一的分析，我们能知道到达第10层的两种情况分别是8到10和9到10，那么就是说

到达第10层的走法=到达第8的走法数量+到达第9层的走法数量

即F(10) = F(9) + F(8)

问题三：既然我们已经知道F(10) = F(9) + F(8)，那么F(9)、F(8)如何求？

这个也很简单，我们假设10层是最后一层，他的走法有F(9) + F(8)种。那么同理我们可以假设9是最后一层，那么他的走法就是前面两层的和，也就是F(8) + F(7)种，第8层也同理。

那么我们就可以得出：

F(9) = F(8) + F(7);
F(8) = F(7) + F(6);
…
F(3) = F(1) + F(2)

这里就体现了动态规划的思想：把一个复杂的问题分阶段的进行简化，逐步简化成简单的问题。

那么当只有1级台阶和2级台阶的时候有几种解法呢？显然是1和2。

所以可以得出：

F(1)=1
F(2)=2
F(n)=F(n-1)+F(n-2) (n>=3)

这一步的核心就是：从后往前推，看和前面有什么的关系

动态规划的三个重要概念

最优子结构、边界、状态转移方程

一、最优子结构

定义：一个问题具有最优子结构性质是指该问题的最优解可以由其子问题的最优解组合而成。也就是说，如果一个问题的最优解包含了子问题的最优解，那么这个问题就具有最优子结构性质。
示例：例如在求解斐波那契数列问题中，斐波那契数列的第(n)项(F(n))可以由(F(n - 1))和(F(n - 2))相加得到。如果我们已经知道了(F(n - 1))和(F(n - 2))的最优解（即它们各自的值），那么就可以通过简单的相加得到(F(n))的最优解。这就体现了斐波那契数列问题具有最优子结构性质。

二、边界

定义：边界是指问题规模最小的情况，在这种情况下可以直接得到问题的解，而不需要再进行进一步的划分和求解。边界条件通常是动态规划算法的起点，它为问题的求解提供了基础。
示例：还是以斐波那契数列为例，当(n = 0)时，(F(0)=0)；当(n = 1)时，(F(1)=1)。这两个值就是斐波那契数列问题的边界条件。在求解斐波那契数列的其他项时，我们可以从这些边界条件开始，逐步推导出更大规模问题的解。

三、状态转移方程

定义：状态转移方程是动态规划算法的核心，它描述了问题的状态之间的转移关系。通过状态转移方程，我们可以从已知的状态推导出未知的状态，从而逐步求解出问题的最优解。
示例：对于斐波那契数列问题，状态转移方程为(F(n)=F(n - 1)+F(n - 2))。这个方程明确了斐波那契数列中不同项之间的关系，我们可以根据这个方程，从边界条件开始，逐步计算出斐波那契数列的其他项。

上面我们知道F(10) = F(9) + F(8)，因此F(9)和F(8)是F(10)的最优子结构
当只有1级台阶或2级台阶的时候，我们可以直接得出结果，无需继续简化。我们称F(1)或者F(2)是问题的【边界】。如果一个问题没有边界，将永远无法得到有限的结果
F(n) = F(n - 1) + F(n - 2)是阶段与阶段之间的状态转移方程。这是动态规划的核心，决定了问题的每一个阶段与下一个阶段的关系

题目求解（从上到下）

递归求解

    public static int climbStairs(int n) {if (n < 1){return 0;}if (n == 1){return 1;}if (n == 2){return 2;}return climbStairs(n - 1) + climbStairs(n - 2);}

备忘录算法

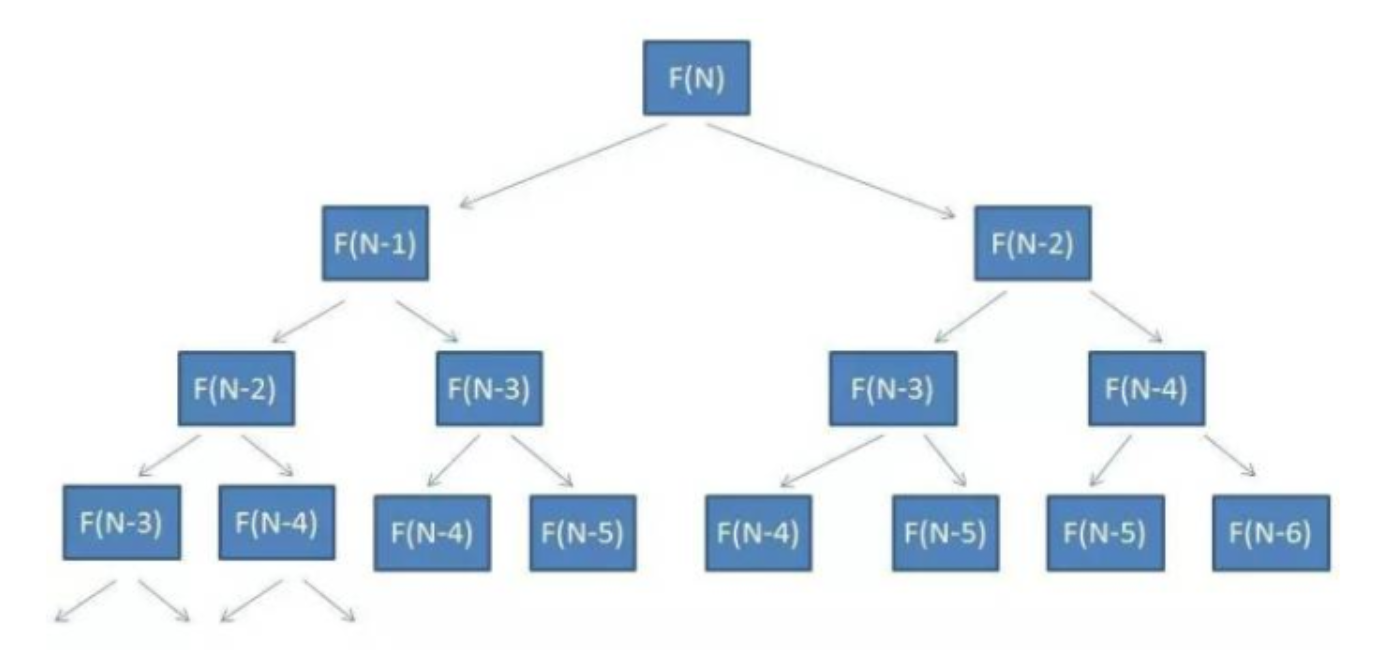
画出二叉树可以发现，有些相同的参数被重复计算了

如果想要避免重复计算，我们可以用创建一个哈希表，每次把不同的参数的计算结果存入哈希。当遇到相同参数时，再从哈希表中取出，就不用重复计算了。这个算法有个专有名词，备忘录算法

class Solution {// 递归时由大量的重复运算，我们可以用一个map把原来算出来的值存起来以便以后使用static Map<Integer, Integer> maps =  new HashMap<Integer, Integer>();public int climbStairs(int n) {if (n < 1){return 0;}if (n == 1){return 1;}if (n == 2){return 2;}if (maps.containsKey(n)){  return maps.get(n);}else{int value = climbStairs(n - 1) + climbStairs(n - 2);maps.put(n, value);return value;}}
}

集合map是一个备忘录。当每次需要计算F(N)的时候，会首先从map中寻找匹配元素。如果map中存在，就直接返回结果，如果map中不存在，就计算出结果，存入备忘录中。

动态规划

动态规划五部曲

确定dp数组以及下标的含义

dp[i]：爬到第i层楼梯，有dp[i]种方法

确定递推公式

从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。

- 首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。
- 还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。

那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！即dp[i] = dp[i - 1] + dp[i - 2]
在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。

dp数组如何初始化

回顾一下dp[i]的定义：爬到第i层楼梯，有dp[i]中方法
需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况。所以本题其实就不应该讨论dp[0]的初始化！
因此，结论是：不考虑dp[0]如果初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。

确定遍历顺序

从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的

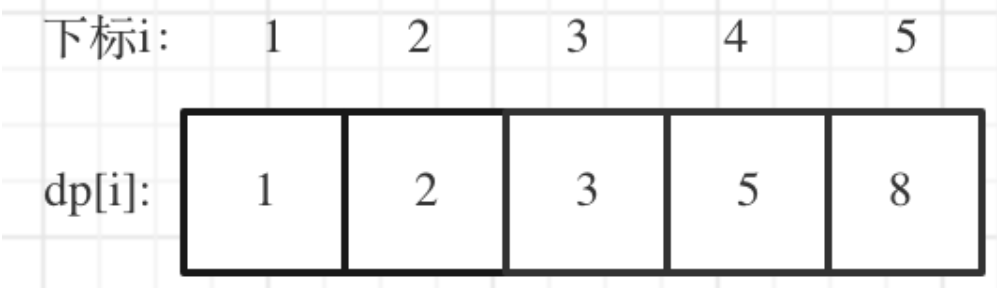
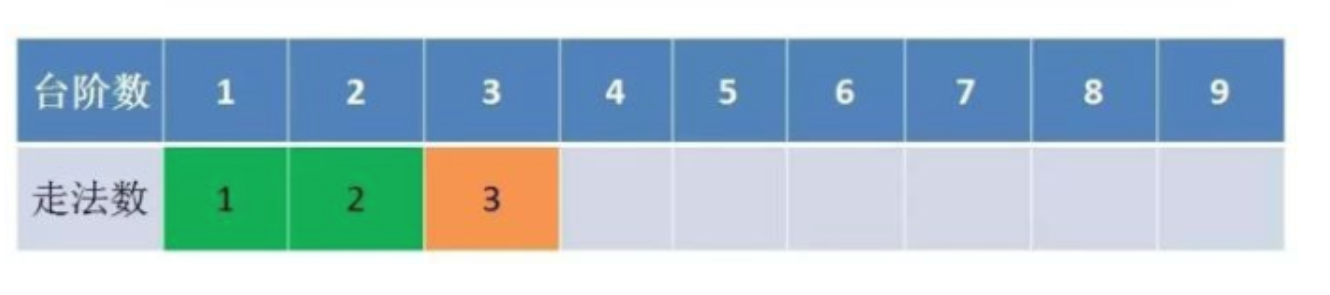
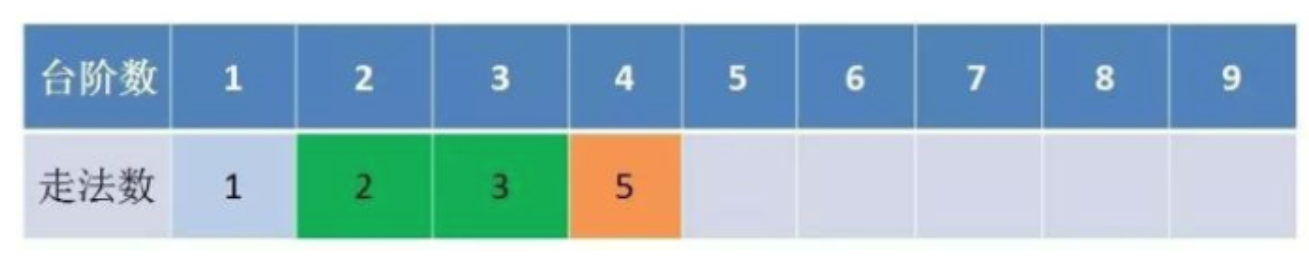
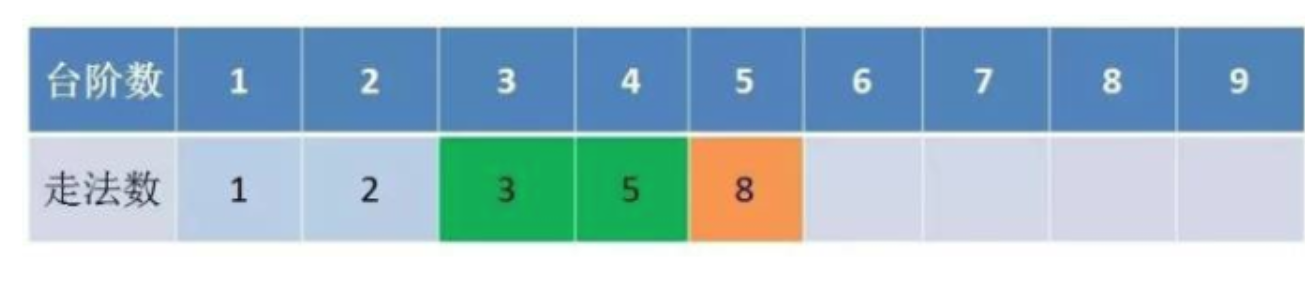
举例推导dp数组

举例当n为5的时候，dp table（dp数组）应该是这样的

代码

class Solution {public int climbStairs(int n) {if(n<=1) return n;int[] dp = new int[n + 1]; // dp[0]不考虑// 含义：第i个台阶有dp[i]种方法dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}

时间复杂度：O ( n )
空间复杂度：O ( n )

动态规划本质上就是填表的过程

类似题目

题目	思路
leetcode：70. 爬楼梯 Climbing Stairs	动态规划
leetcode：746. 使用最小花费爬楼梯 Min Cost Climbing Stairs	动态规划
leetcode：509. 斐波那契数列 Fibonacci Number	动态规划
leetcode：91. 解码方法Decode Ways
leetcode：639.*可以匹配多个字符时，有多少解码方法 II Decode Ways II
leetcode：842. 将数组拆分成斐波那契序列，返回一个成功的组合 Split Array into Fibonacci Sequence	回溯
leetcode：306. 字符串是否能切割成斐波那契序列 Additive Number
leetcode：873. 最长的斐波那契序列长度 Length of Longest Fibonacci Subsequence
Coin Change