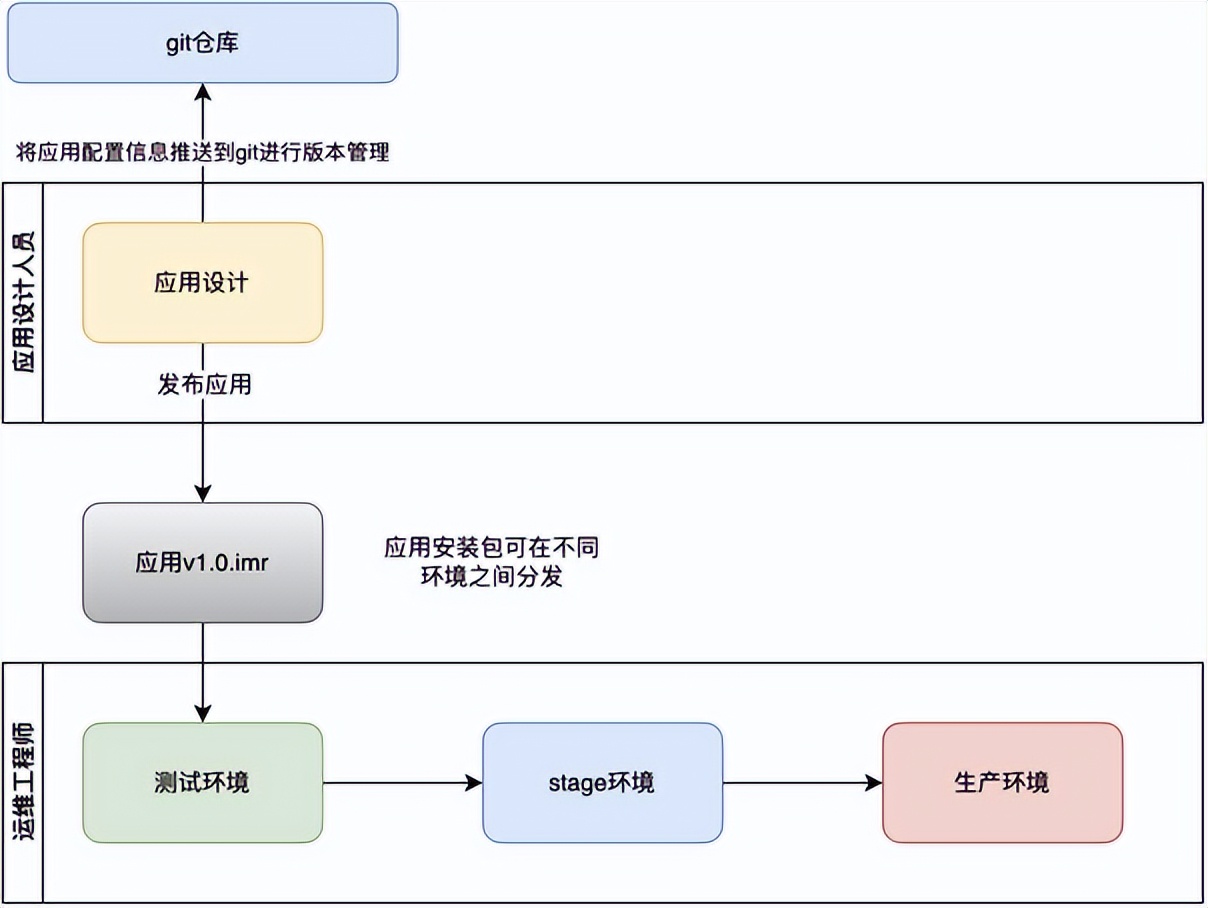
1. 力扣1022：从根到叶的二进制之和

1.1 题目：

给出一棵二叉树，其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。

• 例如，如果路径为 0 -> 1 -> 1 -> 0 -> 1，那么它表示二进制数 01101，也就是 13 。

对树上的每一片叶子，我们都要找出从根到该叶子的路径所表示的数字。

返回这些数字之和。题目数据保证答案是一个 32 位 整数。

 

示例 1：

 

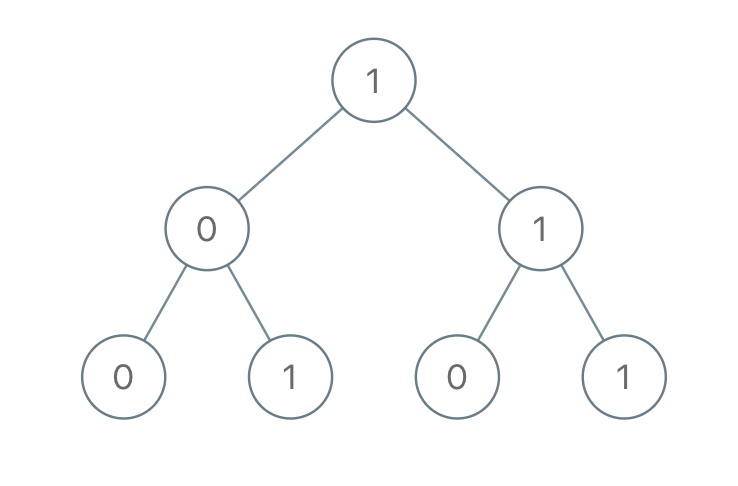
输入：root = [1,0,1,0,1,0,1]
输出：22
解释：(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

示例 2：

输入：root = [0]
输出：0

提示：

• 树中的节点数在 [1, 1000] 范围内
• Node.val 仅为 0 或 1 

1.2 思路：

dfs递归，使用列表来记录从根到叶子节点的路径。递归方法中参数k用来记录该节点在列表中的索引位置，便于到叶子节点的for循环计算。然后继续向左右子树递归，如果其左右子树都处理完了，那么就从列表中删除这个节点的值，

1.3 题解 ：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 全局变量sum记录这些数字之和int sum;// 用列表来记录从根节点到叶子节点走过的路径List<Integer> list = new LinkedList<>();public int sumRootToLeaf(TreeNode root) {dfs(root, 0);return sum;}// 参数列表里的k表示这个节点的值在列表中的索引位置private void dfs(TreeNode node, int k) {if(node == null){return;}list.add(node.val);// 如果是叶子节点，就把列表的二进制数字统计加起来if(node.left == null && node.right == null){int m = 1;for(int i = k; i >= 0; i--){sum += list.get(i)*m;m *= 2;}}// 继续递归dfs(node.left, k+1);dfs(node.right, k+1);// 处理完左右孩子节点后，就将该节点从列表中删除list.remove(k);}
}

代码稍微优化的一下：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 全局变量sum记录这些数字之和int sum;// 用列表来记录从根节点到叶子节点走过的路径List<Integer> list = new LinkedList<>();public int sumRootToLeaf(TreeNode root) {dfs(root, 0);return sum;}// 参数列表里的k表示这个节点的值在列表中的索引位置private void dfs(TreeNode node, int k) {if(node == null){return;}list.add(node.val);// 如果是叶子节点，就把列表的二进制数字统计加起来if(node.left == null && node.right == null){int m = 1;for(int i = k; i >= 0; i--){sum += list.get(i)*m;m *= 2;}}else{// 继续递归dfs(node.left, k+1);dfs(node.right, k+1);}// 处理完左右孩子节点后，就将该节点从列表中删除list.remove(k);}
}

2. 力扣623：在二叉树中增加一行

2.1 题目：

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

• 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
• cur 原来的左子树应该是新的左子树根的左子树。
• cur 原来的右子树应该是新的右子树根的右子树。
• 如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

示例 1:

 

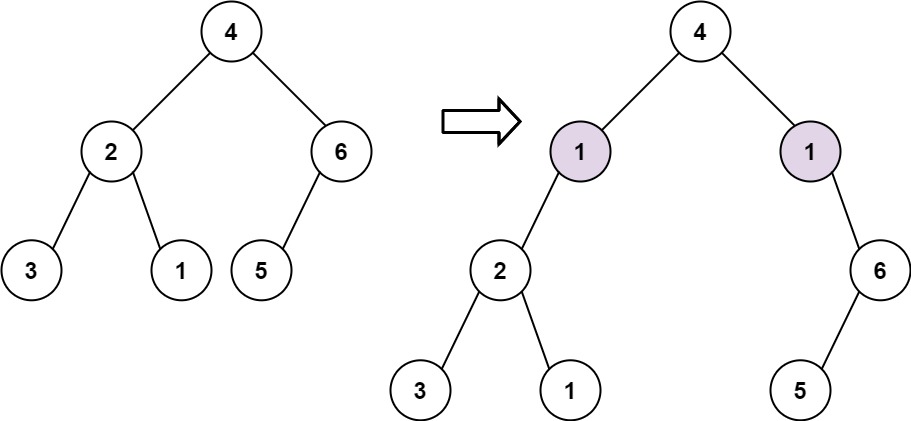
输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]

示例 2

输入: root = [4,2,null,3,1], val = 1, depth = 3
输出:  [4,2,null,1,1,3,null,null,1]

 

提示:

• 节点数在 [1, 104] 范围内
• 树的深度在 [1, 104]范围内
• -100 <= Node.val <= 100
• -105 <= val <= 105
• 1 <= depth <= the depth of tree + 1

2.2 思路：

dfs的思想，总体来说，增加一行有两种情况：

• 在树中间增加一行。
• 在树的最下层的叶子节点的再下一层增加一行。

第一种情况 ，比较好想到，通过dfs的参数k找到要处理的层级节点，然后处理新new的节点与该节点和父亲节点之间的关系。

第二种情况：此时node为null，跟第一种情况的代码几乎完全一样（就不需要处理new节点的孩子 节点的情况）。

2.3 题解：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode addOneRow(TreeNode root, int val, int depth) {// 特殊情况，提前判断即可if(depth == 1){TreeNode node = new TreeNode(val);node.left = root;return node;}dfs(null, root, depth, 1, val);return root;}// k表示该节点在树中的位置private void dfs(TreeNode parent, TreeNode node, int depth, int k, int val) {// 当遍历到叶子节点的左右孩子的时候，如果需要在这一层添加节点的话// 需要作额外操作,做完操作再返回if(node == null){// 比方说叶子节点在第三层，depth在第四层，那么需要在第四层new节点if(depth == k){if(parent.left == node){node = new TreeNode(val);parent.left = node;}else{node = new TreeNode(val);parent.right = node;}}return;}// node不为null的前提下，即对于一般节点的情况// 需要处理新new处理出来的节点与该节点和父亲节点// 三者之间的关系// 处理完直接返回if(k == depth){TreeNode p = new TreeNode(val);if(parent.left == node){p.left = node;parent.left = p;}else{p.right = node;parent.right = p;}return;}// 如果未到时候吗，则递归左右子树dfs(node, node.left, depth, k+1, val);dfs(node, node.right, depth, k+1, val);}
}