一、塑性变形的方式

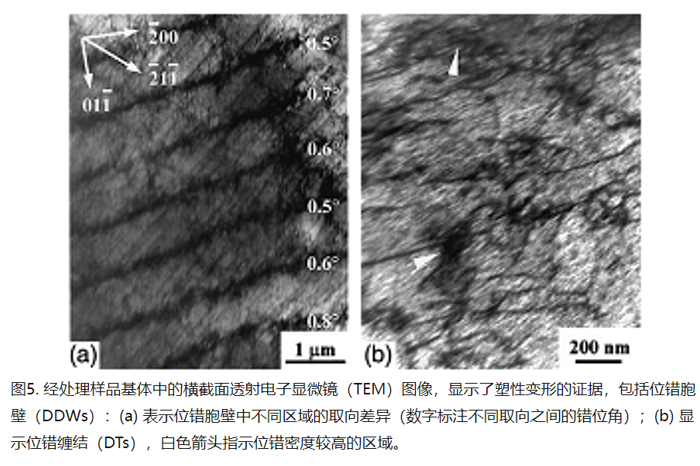
DDWs（Dislocation-Dipole Walls，位错偶极墙）：指由两个位错构成的结构，它们以一种特定的方式排列在一起，形成一个稳定的结构单元。

DTs（Dislocation Tangles，位错纠缠）：指的是材料中由多个位错相互交织和纠缠形成的复杂结构。

1. 塑性变形的方式

金属常见的塑性变形分为滑移和孪生。

滑移

滑移是金属材料切应力的作用下大量位错移动导致晶体的一部分相对于另一部分沿着一定的晶面和晶向产生相对位移不破坏晶体内部原子排列规律的变形。

孪生

孪生是在切应力作用下晶体的一部分相对于另一部分沿一定的晶面和晶向发生均匀切变并形成晶体取向的镜面对称关系。

滑移和孪生的异同*

相同点

1. 切变，切应力，临界分切应力，塑变

2. 沿着一定的晶面、晶向进行

3. 不改变晶体结构

4. 位错运动结果

不同点

	滑移	孪生
晶体位向这个可以通过腐蚀来分辨，如果腐蚀程度一致，则代表晶体位向相同	不改变	改变，形成镜面对称关系
位移量	较大 滑移方向上原子间距的整数倍	较小 小于孪生方向上的原子间距
对塑变的贡献	很大，总形变量大	有限，总形变量小
变形应力/发生条件	有一定的临界分切应力	所需的临界分切应力远高于滑移
变形条件	一般先发生滑移	滑移困难时发生
变形机制	全位错运动的结果	不全位错运动的结果
切变	不均匀切变，只集中在一些滑移面上进行，滑移带之间晶体未发生位移	一部分晶体发生均匀切变，切变区和孪生面平行的每层都发生位移
应力-应变曲线	平缓，光滑，连续	锯齿状

2. 塑性变形的特点

1. 不同时性和不均匀性

各晶粒变形的不同时性和不均匀性是相互联系的。

不同时性：

• 多晶体的各晶粒取向不同，在受到外力时，某些处于软位向的先开始移动。

• 多相合金由于各相晶粒之间力学性能的差异，以及由于晶粒取向不同导致应力状态不同，那些位向有利且应力集中的晶粒先产生塑变。

  

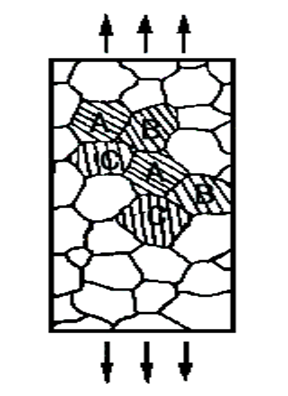
不同时性反映了塑变的局部性，也就是塑变量的不均匀性。

2. 各晶粒变形的相互协调性

多晶体是连续的整体，不可能各个晶粒自由变形，必然会相互约束、相互协调。

二、屈服现象和屈服强度

1. 屈服现象和屈服强度概念

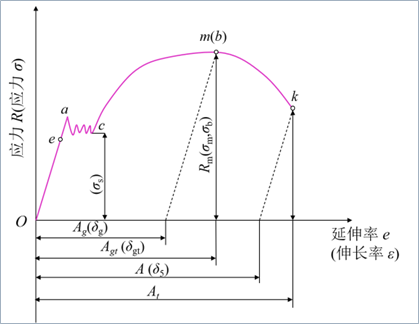
屈服现象：在拉伸过程中，在外力不增加或上下波动的情况下，试样继续伸长变形。

屈服强度：金属呈现屈服现象时，达到塑性变形发生但是应力不增加的应力点。

• 上屈服强度：发生屈服而首次下降前的最大应力，$R_{eH}$。

• 下屈服强度：在屈服期间不计初始瞬时效应（第一次下降）的最小应力，$R_{eL}$。

屈服伸长：屈服过程中产生的伸长。

屈服平台/屈服齿：屈服伸长对应的水平线段或曲折线段。

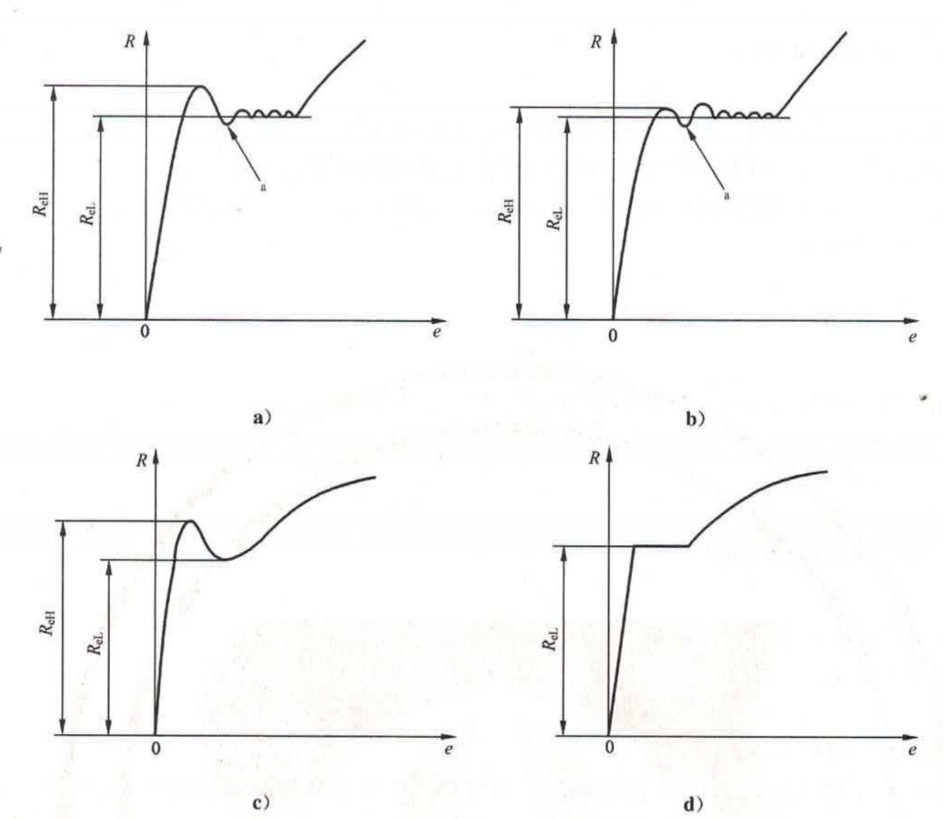
屈服伸长变形不均匀，当外力从屈服阶段最大应力下降到最小应力，试样局部形成与拉伸轴45°的吕德斯带（屈服线），当屈服线布满整个试样，屈服伸长结束，试样进入均匀塑性变形阶段。

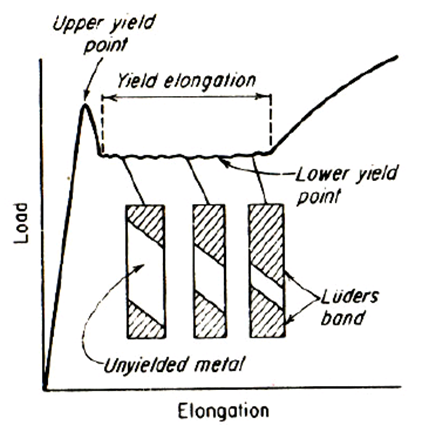
屈服强度表征了材料对微量塑性变形的抗力，一般用下屈服强度$R_{eL}$作为材料屈服强度（$R_{eL}$可重复，可再现）。

屈服强度的计算公式为：

• 上屈服强度：$R_{eH}=\frac{F_{eH}}{S_0}$

• 下屈服强度：$R_{eL}=\frac{F_{eL}}{S_0}$

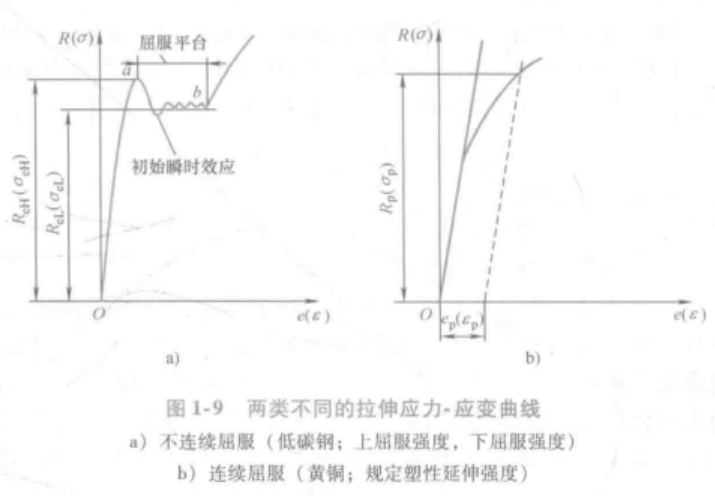
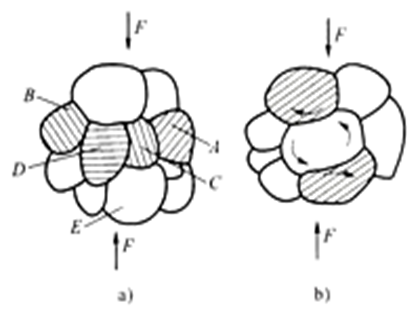
上面提到的都是左图的情况，不连续屈服，有明显屈服现象。但是如果是右图中连续屈服的材料，看不到屈服现象，如何定义其屈服强度？

用规定微量塑性延伸应力表示材料的屈服强度，即拉伸试样产生一定的微量塑性延伸率（0.2%）时对应的应力。

根据测量方法不同，分为三种：

1. 规定塑性延伸强度$R_p$
   

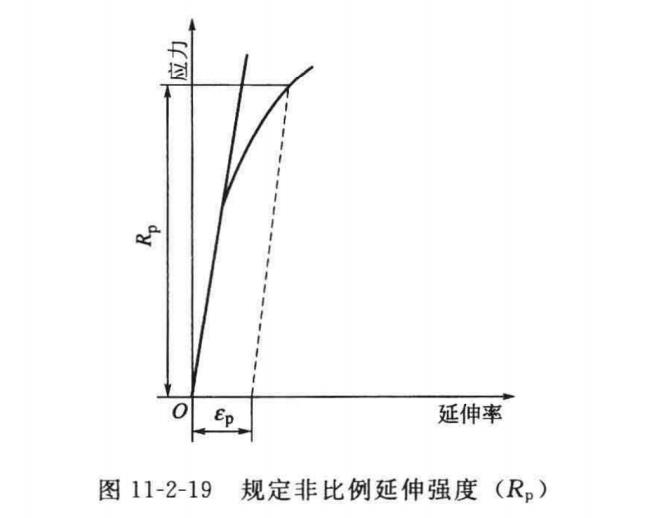
2. 规定残余延伸强度$R_r$
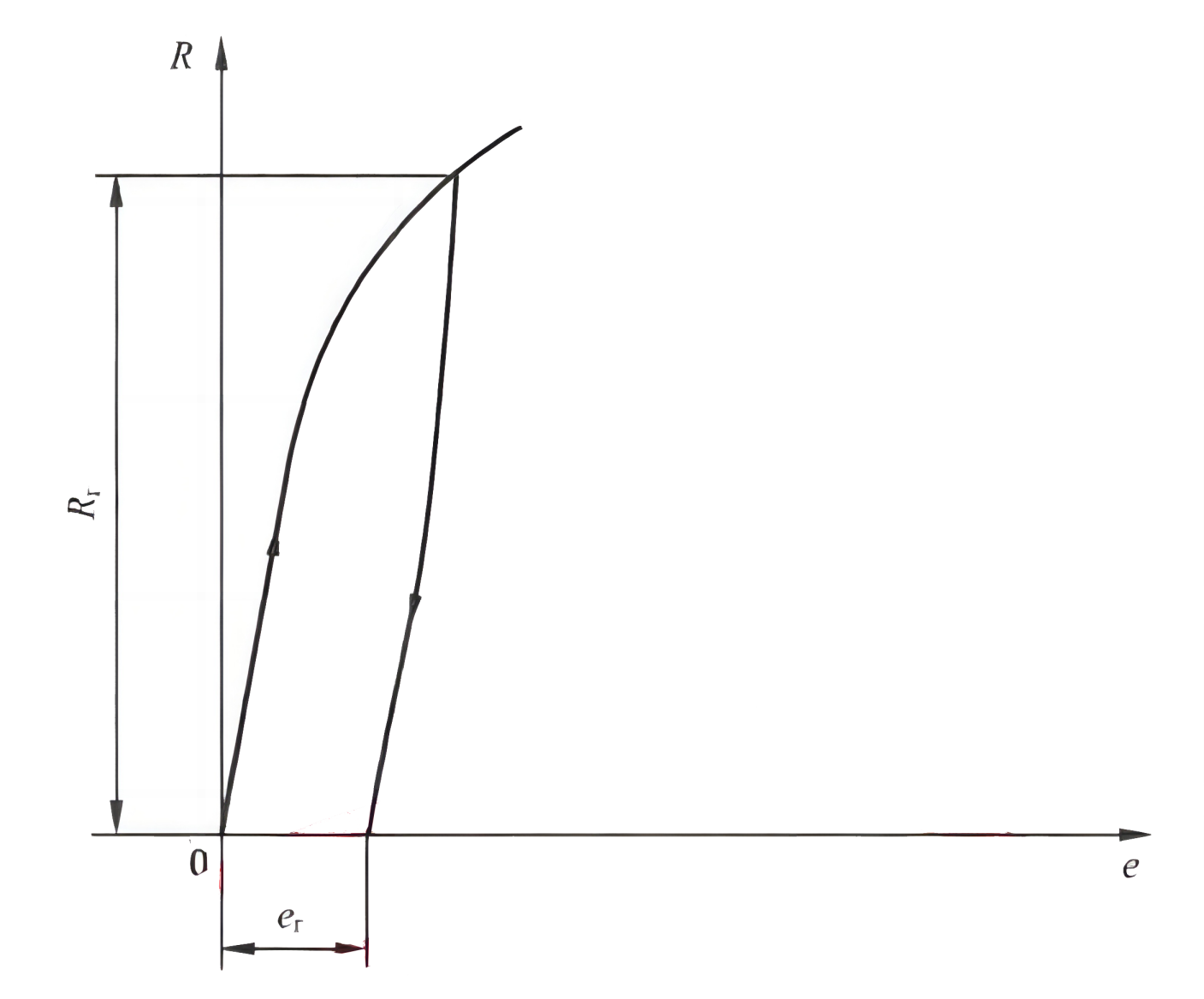   7.png" title=“” alt=“” width=“142”>

3. 规定总延伸强度$R_t$

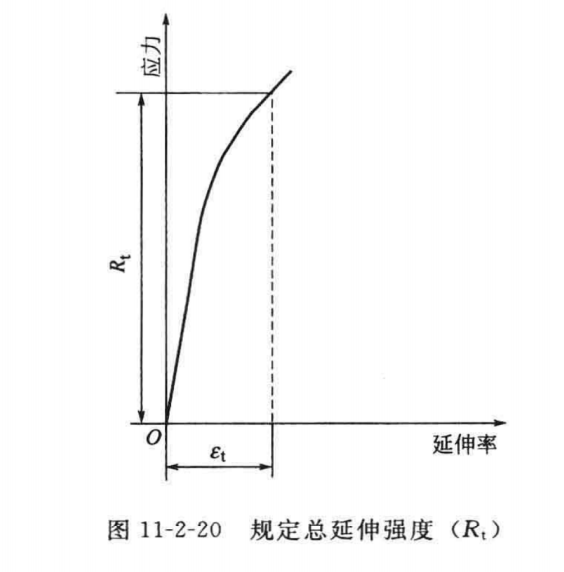
2. 屈服现象发生的三个要素

1. 材料变形前的可动位错密度很小：（或虽然有大量位错，但是被钉扎住：钢的位错被杂质原子或第二相原子钉扎）在变形初期，由于可动位错密度小，材料需要较高的应力才能启动位错的运动，这通常表现为材料的弹性行为。

2. 随塑性变形发生，位错能快速增殖：当材料发生塑性变形时，位错通过弗兰克-里德源（Frank-Read source）机制、双交滑移增殖机制和攀移增殖机制等方式迅速增殖。位错的增殖增加了材料内部的位错密度，这使得进一步的塑性变形更容易发生，因为更多的位错可以参与到塑性变形过程中。

3. 位错运动速率与外加应力有强烈依存关系：位错的运动速率受到外加应力的影响。在较低的应力水平下，位错运动较慢，需要较大的应力才能使位错克服晶格中的障碍（如晶格点阵、其他位错、晶界等）。随着外加应力的增加，位错运动速率加快，塑性变形更容易进行，这导致材料的屈服强度降低。

金属材料塑性变形应变速率$\dot{\epsilon }$和可动位错密度$\rho$、位错运动平均速率$\bar{v}$及伯氏矢量的模b成正比：$\dot{\epsilon }=b\rho \bar{v}$。

上述式子中的$\rho$体现了材料变形前的可动位错密度很小，b体现了随塑性变形发生，位错能快速增殖（因为伯氏矢量的模表示了畸变的程度，塑性变形越大，伯氏矢量的模越大，表明点阵畸变越严重），那么位错运动速率与外加应力有强烈依存关系如何体现？在可动位错密度和伯氏矢量的值已经确定的情况下，怎么通过改变应力来改变位错运动速率，进而提升金属材料的塑性变形应变速率？

位错运动的速率和外加应力的关系式：$\bar{v}=(\frac{\tau }{{\tau }_0}{)}^{m^{\prime }}$
这里的$\tau$是沿滑移面上的切应力，${\tau }_0$是位错以单位速率移动所需的切应力，m‘是位错运动速率应力敏感指数。

欲提高位错运动速率，需要一个较高的应力（上屈服强度）。一旦塑性变形产生，位错大量增值（ρ增加），位错平均运动速率必然下降，相应的应力也就降低，从而产生屈服现象。

3. 屈服强度作用

屈服强度是金属材料重要的力学性能指标，是从静强度角度选择材料的依据。

1、 作为防止因材料过量塑性变形而导致机件失效的设计和选材的依据；
2 、根据屈服强度与抗拉强度的比值（屈强比）的大小，衡量材料进一步产生塑性变形的倾向，作为材料冷塑性变形加工和确定机件缓解应力集中防止脆性断裂的参考依据。

屈服强度是机件开始塑性变形的强度设计准则。屈服强度高，提高了许用应力，减轻了零件或构件的重量，减小零件尺寸和体积，但是对缺口敏感，脆性增加；屈服强度低，冷加工成型性能和焊接性能好，所以要选最佳值。

传统的强度设计方法：

许用应力$[\sigma ]=\frac{{\sigma }_s}{n}$，若是韧性材料，要求n≥2；若是脆性材料，要求n=6。

4. 影响屈服强度的因素

（一）、影响屈服强度的内在因素

金属本性及晶格类型

不同晶格间的晶格阻力不同，因此，造成了屈服强度的不同。

晶格阻力即派纳力——在理想晶体中仅存在一个位错运动时所需克服的阻力，和伯氏矢量以及位错宽度有关。

派纳力${\tau }_{p-n}$公式：${\tau }_{p-n}=\frac{2G}{1-\nu }{e}^{-\frac{2\pi a}{b(1-\nu )}}$（$\nu$是泊松比，$a$是滑移面的晶面间距，b是伯氏矢量的模【原子间距的整数倍】，$\omega =\frac{a}{1-\nu }$是位错宽度）或者$\tau =\frac{\alpha Gb}{L}$（α为比例系数，L是位错间距离）。

要想派纳力小，就要晶面间距大、伯氏矢量小、位错宽度大，位错间距离小。

晶粒大小和亚结构

晶粒大小将影响晶界的分布，从而影响位错的运动阻力。

细晶强化理论Hall-Petch公式（屈服强度与晶粒大小之间的关系）：${\sigma }_s={\sigma }_i+k_y{d}^{-1/2}$（${\sigma }_i$ 表示位错运动的总阻力【摩擦阻力】，d是晶粒平均直径）

减少晶粒尺寸，增加位错运动障碍，屈服强度提高。

亚晶界的作用和晶界类似，都是阻碍位错运动。

溶质元素

固溶强化：往纯金属里加溶质原子（间隙+置换）形成固溶合金，提高屈服强度。

间隙固溶体＞置换固溶体

第二相

1.第二相强化效果和质点能否在屈服变形中变形有关：

• 可变形第二相质点（时效铝合金GP区中的θ〞相）

• 不可变形的第二相质点（钢铁材料：碳化物、氮化物等）

机制：当运动着的位错遇到滑移面上的第二相粒子时，或切过（沉淀强化） 或绕过（弥散强化），滑移变形才能进行。这一过程需要消耗额外的能量，而需要提高外加应力，造成强化。

沉淀强化（时效强化）precipitation strengthening ：可变形，与母相有共格关系，又叫时效强化相。通过过饱和固溶体的时效处理而沉淀析出来的。（合金化加淬火时效，造成理想的沉淀相。）
弥散强化dispersion strengthening：不参与变形，与基体非共格关系，不溶于基体。（利用碳化物做弥散相，不参与变形）

1. 沉淀强化：这种强化方式涉及到在金属材料中形成第二相粒子，这些粒子可以是金属间化合物、碳化物、氮化物等。沉淀强化通常通过时效热处理来实现，即在固溶处理后，将材料放置在一定的温度下保持一段时间，使得溶质原子偏聚并形成细小的第二相粒子。这些粒子可以阻碍位错的运动，从而提高材料的强度。沉淀强化的强化效果与沉淀相的尺寸、分布、数量以及与基体的匹配程度有关。沉淀强化适用于多种合金体系，特别是那些可以通过时效处理来优化微观结构的材料。

2. 固溶强化：固溶强化是通过将合金元素溶解在基体金属中来实现的。这些合金元素可以是间隙型或置换型，它们的加入会导致晶格畸变，从而增加位错运动的阻力。固溶强化的效果取决于合金元素的浓度、原子尺寸差异、价电子数差异等因素。固溶强化通常适用于那些可以通过合金化来提高性能的材料。

3. 弥散强化：弥散强化是通过在材料中均匀分散硬质颗粒来实现的。这些颗粒通常是高熔点的氧化物、碳化物或氮化物，它们不溶于基体金属。弥散强化的颗粒尺寸很小，通常通过粉末冶金方法制造。这些硬质颗粒可以有效地阻碍位错的运动，从而提高材料的强度和硬度。弥散强化适用于那些需要在高温下保持强度的材料。

位错切过机制

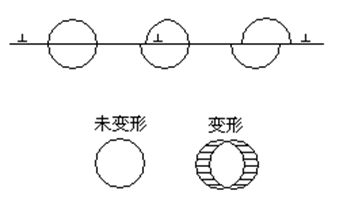
当第二相粒子与基体保持共格关系、尺寸较小、有一定塑性、可以变形的情况下，位错可以通过切过粒子来实现强化。位错在切过粒子时，会生成新的表面，增加表面能，同时可能产生反相畴界、割阶等，这些都会阻碍位错的运动，从而提高材料的强度。位错切过机制通常涉及到共格应变、化学有序、模量差异等因素，这些因素共同作用使得位错运动受阻，增加材料的强度。

位错绕过机制（奥罗万机制）

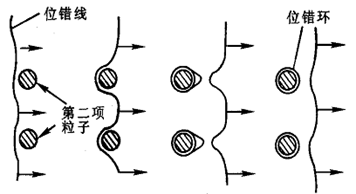
当第二相粒子不可变形时，位错在运动过程中会受到粒子的阻挡而发生弯曲，产生反向应力，当应力达到一定程度时，位错会绕过粒子继续前进。在这个过程中，位错线会绕过粒子，恢复原态，继续向前滑移。位错每绕过粒子一次，会在粒子周围留下位错环，这些位错环的存在使得后续位错绕过粒子更加困难，导致流变应力增加，从而提高材料的强度。

2.第二相强化考虑因素：第二相的大小、数量、形态（片状珠光体和球状珠光体）、分布以及性能等。
3.热处理工艺及参数

4.合金元素种类及含量。
合金元素的作用主要是为形成所需要的第二相粒子提供成分条件。

（二）、影响屈服强度的外部因素

温度的影响

温度升高，屈服强度降低。

应变速率的影响

应变速率越快，屈服强度越大。——应变速率硬化

应力状态的影响

切应力分量越大，越有利于塑性变形

扭转强度 < 拉伸强度 < 弯曲强度

三、应变硬化

在金属整个变形过程中，当外力超过屈服强度以后，塑性变形并不像屈服平台那样连续流变下去，而是需要不断增加外力才能继续进行，这表明金属材料有一种阻止连续变形的能力，这就是应变硬化性能。

加工硬化效应(Work-Hardening Effect)

随着塑性变形程度的增加，晶体对滑移的阻力愈来愈大。从位错理论的角度看，其主要原因是位错运动愈来愈困难。滑移变形的过程就是位错运动的过程，如果位错不易运动，就是材料不易变形，也就是材料强度提高，即产生了加工硬化。

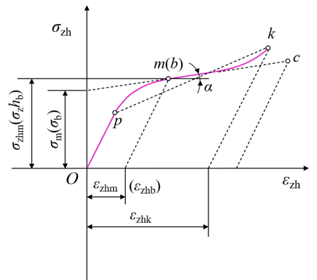
真实应力—应变曲线上，PB为均匀塑性变形阶段，在此阶段，应力与应变之间满足Hollomon关系式：${\sigma }_{zh}=K{\epsilon }_{zh}^n$其中，${\sigma }_{zh}$为真实应力，${\epsilon }_{zh}$为真实应变，n为应变硬化指数（n反映了金属抵抗均匀塑性变形的能力，体现材料应变硬化行为的性能指标。n=1表示材料是理想的弹性体，因为应力应变成正比。一般金属材料的n在0.1~0.5之间），K为硬化系数。

应变硬化指数n工程意义

1、加工硬化对金属材料的使用也是有利的，n越大，则机件承受偶然过载的能力越大。
例如构件在承受负荷时，尽管局部区域负荷超过了屈服强度，金属发生塑性变形，但通过加工硬化，这部分金属可以承受这一负荷而不发生破坏，并把部分负荷转嫁给周围受力较小的金属，从而保证构件的安全。（比如吊钩）

2、应变硬化指数n对金属材料的冷变形工艺有重要影响

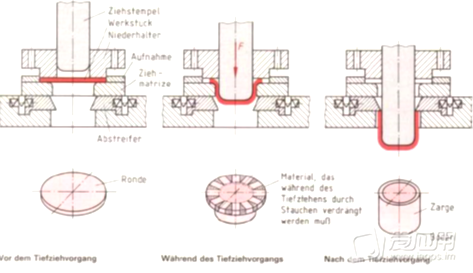
如拉丝时已通过拉丝模的金属截面积变小，因而作用在这一较小截面积上的单位面积拉力比原来大，但是由于加工硬化，这一段金属可以不继续变形，反而引导拉丝模后面的金属变形，从而才能进行拉拔；又如冲压时已变形部分的金属由于加工硬化不再变形，而让较软的未变形部分变形，从而才能实现冲压时的均匀变形。

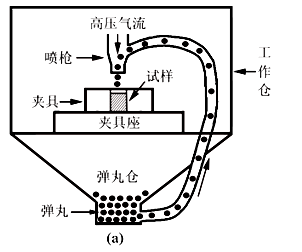
3、表面强化

向表面喷弹丸，表面发生塑性变形进而加工硬化。

四、缩颈和抗拉强度

（一）缩颈现象

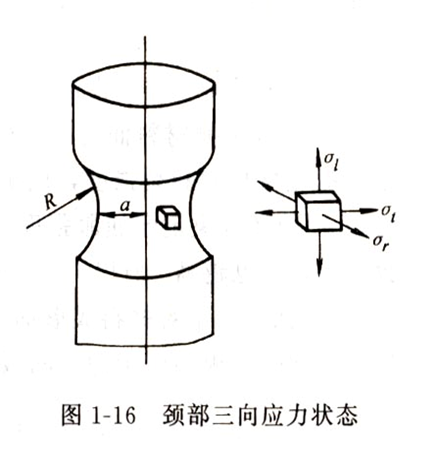
缩颈是韧性金属材料在拉伸试验时变形集中于局部区域的现象，他是应变硬化和截面减小共同作用的结果。应力状态由均匀变形时的单轴应力状态转变为三轴应力状态。

（二）缩颈判据

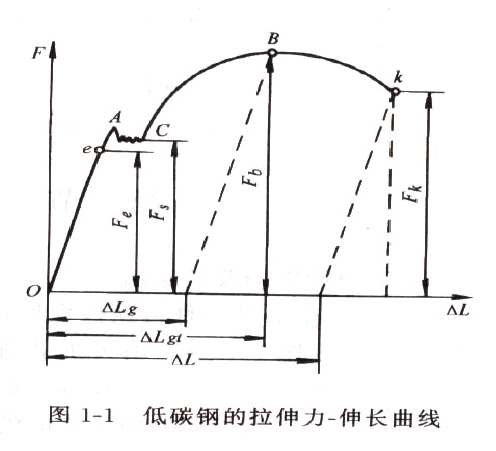
回到前面的力-伸长曲线，在到达F的最大点B之前，试样进行均匀塑性变形，dF＞0；但是到B点后，开始颈缩，dF＜0。故颈缩的判据应为dF=0。

dF=0：

$$\begin{gathered} dF=0 \\ F={\sigma }_{zh}S \\ dF=Sd{\sigma }_{zh}+{\sigma }_{zh}dS=0 \\ \frac{dS}{S}=-\frac{d{\sigma }_{zh}}{{\sigma }_{zh}} \end{gathered}$$

因为塑性变形时体积不变dV=0，所以：

$$\begin{gathered} dV=0 \\ V=SL \\ dV=LdS+SdL=0 \\ -\frac{dS}{S}=\frac{dL}{L}=d{\epsilon }_{zh}=\frac{d\epsilon }{1+\epsilon } \end{gathered}$$

综上，缩颈判据为：${\sigma }_{zh}=\frac{d{\sigma }_{zh}}{d{\epsilon }_{zh}}$。当真实应力-应变曲线上某点的斜率（应变硬化速率）等于该点的真实应力，缩颈产生。

在缩颈点仍满足Hollomon关系，把${\sigma }_{zh}=K{\epsilon }_{zh}^n$求导得$d{\sigma }_{zh}=nK{\epsilon }_{zh}^{n-1}=K{\epsilon }_{zh}^n$，所以：${\epsilon }_{zh}=n$。当金属材料的应变硬化指数等于最大真实均匀塑性应变量时，颈缩产生。

（三）缩颈颈部应力修正

为了修正缩颈处产生的三向应力状态而进行的修正。Bridgman Relation ( P. W. Bridgman, 1944)

为了补偿颈部径向应力、切向应力对轴向应力的影响，求得仍然是均匀轴向应力状态的真实应力，以得到真正的真实应力—应变曲线，必须对颈部应力进行修正：

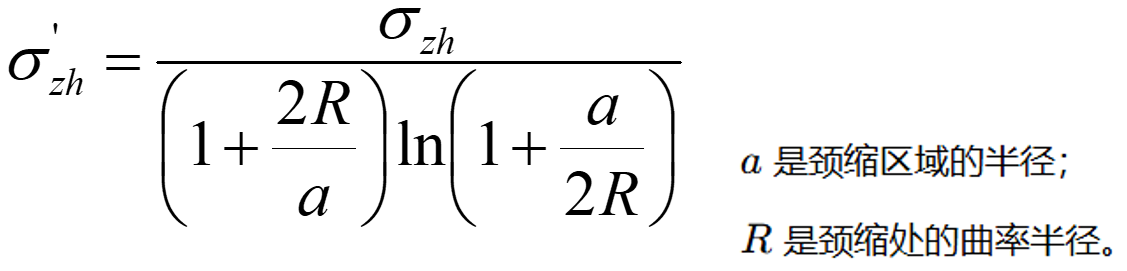
（四）抗拉强度

抗拉强度是材料在受到拉伸力作用时抵抗破坏的最大能力，它表示材料在拉力作用下的最大承受能力。

UTS (Upper Tensile Strength)：${\sigma }_b=\frac{F_b}{A_0}$

强度意义

o1、产品规格说明或质量控制指标；

o2、对于脆性材料，${\sigma }_b$作为产品设计判据；

o3、${\sigma }_b$的高低决定于屈服强度和应变硬化指数；

o4、${\sigma }_b$与布氏硬度、疲劳极限之间有一定的经验关系。

五、塑性

               均匀塑性（应变强化阶段）变形

塑性变形

               集中塑性（缩颈阶段）变形

金属材料断裂前所产生的塑性变形由均匀塑性变形和集中塑性变形两部分构成。大多数拉伸时形成缩颈的韧性金属材料，其均匀塑性变形量比集中塑形变形量要小得多，一般均不超过集中变形量的50%。

（一）塑性变形指标

1. 断后伸长率：

金属材料常用的塑性指标为断后伸长率和断面收缩率。断后伸长率是试样拉断后标距的伸长与原始标距的百分比：

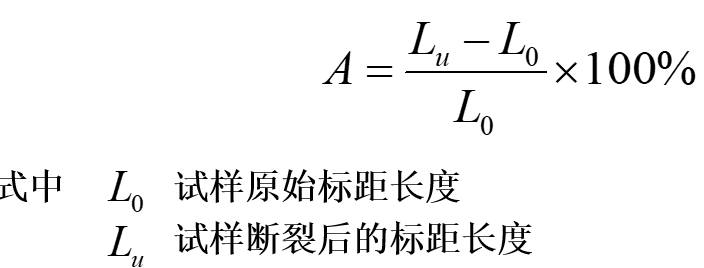
2. 断面收缩率

断面收缩率是试样拉断后，缩颈处横截面积的最大缩减量与原始横截面积的百分比，用符号Z 表示

（二）塑性意义

1、防止机件偶然过载突然产生破坏；

2、塑形可以松弛裂纹尖端的局部应力，有利于阻止裂纹扩展；

3、塑形对金属的成型加工至关重要；

4、机器装配安装、修复工序顺利完成也需要材料具有一定的塑形；

5、反应冶金质量的优劣，评定材料的质量。

静力韧度（强塑积）

韧度是度量材料韧性的力学性能指标，其中又分静力韧度、冲击韧度和断裂韧度。习惯上，韧性和韧度这两个名词常常混用。

韧性是金属材料的力学性能，它是指金属材料断裂前吸收塑性变形功和断裂功的能力，或指材料抵抗裂纹扩展的能力。金属材料在静拉伸时单位体积材料断裂前所吸收的功定义为静力韧度，它是强度和塑性的综合指标。测出材料真实应力—应变曲线下包围的面积，可以精确获得静力韧度值。但工程上用近似计算方法，如对韧性材料的静力韧度表示如下：

静力韧度对于按屈服强度设计，而在服役中有可能遇到偶然过载的机件如链条、起重吊钩等，是必须考虑的重要指标。