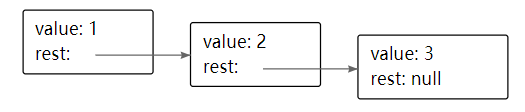简易STL实现 | 红黑树的实现

1、原理

红黑树（Red-Black Tree）是一种自平衡的二叉搜索树
红黑树具有以下特性，这些特性保持了树的平衡：

节点颜色：每个节点要么是红色，要么是黑色
根节点颜色：根节点是黑色的。
叶子节点（NIL 节点）颜色：所有叶子节点（NIL 节点）都是黑色的
相邻节点颜色：如果一个节点是红色的，则它的两个子节点都是黑色的
路径黑高度相等：从任意节点到其每个叶子节点的简单路径上，黑色节点的数量相同

在最坏情况下的查找、插入和删除操作的时间复杂度都是 O(log n)

1.1 节点结构

键值（Key）：保存实际数据的值，用于比较和排序
颜色信息：用于红黑树的平衡，标记节点的颜色
左子节点和右子节点指针：指向左右子节点的指针
父节点指针：指向父节点的指针

1.2 插入操作

定位插入位置：从根节点开始，按照二叉查找树的规则，找到合适的插入位置
插入新节点：在插入位置创建一个新节点，并将其颜色设为红色
修复红黑树性质：如果新节点的父节点是红色，需要通过一系列旋转和重新着色操作来保持红黑树的平衡

1.3 删除操作

标记节点：将要删除的节点标记为“被删除”，而不是立即删除它
删除节点：根据情况删除节点，并用子节点替代它的位置
修复红黑树性质：如果删除的节点是黑色或替代节点是红色，或者删除的节点是根节点，可能需要通过一系列旋转和重新着色操作来保持红黑树的平衡

2、代码实现

#include <iostream>
#include <sstream>
#include <string>enum class Color { Black, Red }; // 最后加分号template <typename Key, typename Value> // 两个typename
class RedBlackTree {class Node {public:Color color;Key key; // 比较和排序的依据Value value;Node* left;Node* right;Node* parent;Node():color(Color::Black), left(nullptr), right(nullptr), parent(nullptr) {// 只初始化了部分变量}// 注意使用Color中定义类型的办法// 如果枚举类型的值较小，直接传递值的开销非常低（不涉及昂贵的拷贝操作）// 对于像 int 或 enum 这样的小型数据类型，直接传值的成本很低，甚至比传递引用更有效（引用本质上是一个隐式指针）。因为传递引用（或指针）涉及额外的间接访问，可能引发更多的内存访问操作或指针解引用的开销Node(const Key& k, const Value& v, Color c, Node* p = nullptr): key(k), value(v), color(c), left(nullptr), right(nullptr), parent(p) {}};Node* root;size_t size;Node* Nil;// 查询结点（通过key)Node* lookUp(const Key& key) {Node* currNode = root;while (currNode) {if (currNode->key == key) {return currNode;}else if (currNode->key > key) {currNode = currNode->left;}else {currNode = currNode->right;}}return currNode;}// 左旋，旋转就是3个过程void leftRotate(Node* cur) {Node* rSon = cur->right;// if (rSon != nullptr) rSon / cur 为nullptr转不了了rSon->parent = cur->parent;if (!cur->parent) { // 注意先判断是否为空，再使用指针root = rSon;}else if (cur->parent->left == cur) {cur->parent->left = rSon;}else if (cur->parent->right == cur) {cur->parent->right == rSon;}cur->parent = rSon;cur->right = rSon->left;if (rSon->left)rSon->left->parent = cur;rSon->left = cur;}// 右旋void rightRotate(Node* cur) {Node* lSon = cur->left;if (!cur->parent) {root = lSon;}else if (cur->parent->left == cur) {cur->parent->left = lSon;}else if (cur->parent->right == cur) {cur->parent->right = lSon;}lSon->parent = cur->parent;cur->parent = lSon;cur->left = lSon->right;if (lSon->right) {lSon->right->parent = cur;}lSon->right = cur;}// 插入修正void insertFix(Node* cur) {if (cur->parent && cur->parent->color == Color::Red) {// 只有父结点是红色才需要调整if (cur->parent->parent && cur->parent->parent->left == cur->parent) {// 1.1 & 1.2if (cur->parent->parent->right->color == Color::Red) {// 1.1cur->parent->color = Color::Black;cur->parent->parent->right->color = Color::Black;cur->parent->parent->color = Color::Red;insertFix(cur->parent->parent);}// 1.2else if (cur->parent->parent->right == nullptr || cur->parent->parent->right->color == Color::Black) {if (cur->parent->right == cur) {leftRotate(cur->parent);}cur->parent->color = Color::Black;cur->parent->parent->color = Color::Red;rightRotate(cur->parent->parent);}}else if (cur->parent->parent && cur->parent->parent->right == cur->parent) {// 2.1 && 2.2 if (cur->parent->parent->left->color == Color::Red) {// 2.1cur->parent->color = Color::Black;cur->parent->parent->left->color = Color::Black;cur->parent->parent->color = Color::Red;insertFix(cur->parent->parent);}// 2.2else if (cur->parent->parent->left == nullptr || cur->parent->parent->left->color == Color::Black) {if (cur->parent->right == cur) {leftRotate(cur->parent);}cur->parent->color = Color::Black;cur->parent->parent->color = Color::Red;leftRotate(cur->parent->parent);}}}root->color = Color::Black; // 确保根节点一定是黑色的}// 插入节点void insertNode(const Key& key, const Value& value) {Node* tar = new Node(key, value, Color::Red);Node* cur = root;if (cur == nullptr) { // 加入的第一个节点root = tar;}Node* par = nullptr;while (cur) {par = cur;if (cur->key > tar->key)cur = cur->left;else if (cur->key < tar->key)cur = cur->right;else {// 最后相等的时候，不插入了delete tar;return;}}size++;if (par) {if (par->key > key) {par->left = tar;tar->parent = par;}else {par->right = tar;tar->parent = par;}}insertFix(tar);}// 中序遍历void inorderTraverse(Node* cur) {if (cur) {inorderTraverse(cur->left);std::cout << cur->key << " ";std::cout << cur->value << " ";inorderTraverse(cur->right);}}// 下面进行删除相关的操作，删除需要用到 Nil哨兵// 辅助函数 是为了处理删除中特有的遇到空节点情况// 辅助函数，获取颜色，使空指针变为黑色Color getColor(Node* cur) {if (cur == nullptr) {return Color::Black;}elsereturn cur->color;}// 辅助函数，设置颜色void setColor(Node* cur, Color col) {if (cur == nullptr) {return;}cur->color = col;}// 辅助函数，断开与哨兵的连接void disconnectNil() {if (Nil == nullptr) {return;}if (Nil->parent != nullptr) {if (Nil->parent->left == Nil) {Nil->parent->left = nullptr;}else {Nil->parent->right = nullptr;}}}// 辅助函数，用新结点替换旧结点void replaceNode(Node* oldNode, Node* newNode) {if (!oldNode->parent) {root = newNode;}else if (oldNode->parent->left == oldNode) {oldNode->parent->left = newNode;newNode->parent = oldNode->parent;}else {oldNode->parent->right = newNode;newNode->parent = oldNode->parent;}// 不考虑孩子节点，因为后面处理不同}// 辅助函数，寻找以某个节点为根结点的子树中的最小结点Node* findMin(Node* cur) {while (cur->left) {cur = cur->left;}return cur;}// 删除修正，需要哨兵Nil// 删除修正四种情况的核心是：兄弟结点的子节点有没有红色结点（有红节点转到父结点的位置上就OK了，如果到根结点还是没有也OK了）？之后是兄弟节点有没有红色节点 /  兄弟结点子节点的红色节点在哪void removeFix(Node* cur) { // cur就是xwhile (cur != root && getColor(cur) == Color::Black) // 一旦碰到红的就结束了{// 先处理图中所示的左边的情况，右边是对称的if (cur->parent->left == cur) {if (getColor(cur->parent->right) == Color::Red) { // (a)转(b)/(c)/(d)setColor(cur->parent, Color::Red);setColor(cur->parent->right, Color::Black);leftRotate(cur->parent);}else if (getColor(cur->parent->right->left) == Color::Black && getColor(cur->parent->right->right) == Color::Black) {setColor(cur->parent->right, Color::Red);cur = cur->parent;}else if (getColor(cur->parent->right->left) == Color::Red && getColor(cur->parent->right->right) == Color::Black) {setColor(cur->parent->right, Color::Red);setColor(cur->parent->right->left, Color::Black);rightRotate(cur->parent->right);}else {setColor(cur->parent->right, getColor(cur->parent));setColor(cur->parent, Color::Black);setColor(cur->parent->right->right, Color::Black);leftRotate(cur->parent);}}else {Node* bro = cur->parent->left;if (getColor(bro) == Color::Red) { // (a)转(b)/(c)/(d)setColor(cur->parent, Color::Red);setColor(bro, Color::Black);rightRotate(cur->parent);}else if (getColor(bro->left) == Color::Black && getColor(bro->right) == Color::Black) {setColor(bro, Color::Red);cur = cur->parent;}else if (getColor(bro->left) == Color::Red && getColor(bro->right) == Color::Black) {setColor(bro, Color::Red);setColor(bro->left, Color::Black);rightRotate(bro);}else {setColor(bro, getColor(cur->parent));setColor(cur->parent, Color::Black);setColor(bro->right, Color::Black);rightRotate(cur->parent);}}}setColor(cur, Color::Black);}void deleteNode(Node* tar) {Color oriColor = tar->color; // 被删除的颜色（不一定就是被删除结点的颜色）Node* adjust = nullptr; // 调整的结点Node* parentRP = nullptr;// 1.对于删除结点同时有左右子节点的，记录替代结点代替之前位置的父结点，为插入Nil结点做准备// 2.对于删除结点只有一个子节点的，显然不能记录代替之前的父结点（就是被删除的那个），应该使用删除节点的父结点if (!tar->left) {adjust = tar->right;parentRP = tar->parent;//2replaceNode(tar, tar->right);oriColor = getColor(tar->right); // 始终记录替代节点的颜色}else if (!tar->right) {adjust = tar->left;parentRP = tar->parent;//2replaceNode(tar, tar->left);oriColor = getColor(tar->left);}else {Node* nextNode = findMin(tar->right); // 后继节点oriColor = getColor(nextNode);if (nextNode == tar->right) {// 如果替代节点是删除节点的直接右孩子// 不需要把替换节点和替换 替换节点 两部分分开来，一起干就行adjust = nextNode->right; // 替换 替换节点 调整的结点replaceNode(tar, tar->right);// 处理替换结点的子节点nextNode->left = tar->left;if (nextNode->left)nextNode->left->parent = nextNode; // 任何更改肯定是两句话parentRP = nextNode->parent;//1}else if (!tar->parent) // 删除的结点是根结点 {root = tar;tar->parent = nullptr;}else {// 两步：替换节点和替换 替换节点// 替换 替换节点replaceNode(nextNode, nextNode->right);// 替换节点，处理替换结点的子节点replaceNode(tar, nextNode);// 右子节点nextNode->right = tar->right;tar->right->parent = nextNode;// 左子节点nextNode->left = tar->left;tar->left->parent = nextNode;parentRP = nextNode->parent;//1}// 如果替代节点存在，更新其颜色为删除节点的颜色if (nextNode != nullptr) {nextNode->color = tar->color;}// 如果替代节点不存在，将删除节点的颜色赋给origCol变量else {oriColor = tar->color;}}if (oriColor == Color::Black) {if (adjust == nullptr)removeFix(adjust);// Nil节点是黑色： Nil节点默认是黑色的，这是红黑树的基本性质之一。所有的空节点（叶子节点的左右孩子）都被视为黑色节点// 根据红黑树的定义，在删除节点时，如果替换的子节点是Nil，它依然保持黑色，从而不破坏黑色节点的数量，也就不会破坏红黑树的性质// 为了能顺利插入虚拟Nil叶子结点，所以 需要时刻保持记录 替代节点的父节点else {Nil->parent = parentRP;// 如果替代节点的父节点存在，设置其对应的孩子指针为Nil节点if (parentRP != nullptr) {if (parentRP->left == nullptr) {parentRP->left = Nil;}else {parentRP->right = Nil;}}// 进行修复操作removeFix(Nil);// 断开Nil节点与树的连接，因为在红黑树中Nil节点通常是单独存在的disconnectNil();}}// 删除节点delete tar;}
public:// 构造函数RedBlackTree() : root(nullptr), size(0), Nil(new Node()) {Nil->color = Color::Black; // Nil指针的颜色始终是黑色的}// 插入void insert(const Key& key, const Value& value) { insertNode(key, value); }// 删除void remove(const Key& key) {Node* nodeToBeRemoved = lookUp(key);if (nodeToBeRemoved != nullptr) {deleteNode(nodeToBeRemoved);size--;}}Value* at(const Key& key) {auto ans = lookUp(key);if (ans != nullptr) {return &ans->value;}return nullptr;}int getSize() { return size; }bool empty() { return size == 0; }// 中序遍历打印void print() {inorderTraverse(root);std::cout << std::endl;}void clear() {deleteNode(root);size = 0;}// 析构函数~RedBlackTree() {// 释放节点内存deleteTree(root);}private:// 递归释放节点内存void deleteTree(Node* node) {if (node) {deleteTree(node->left);deleteTree(node->right);delete node;}}};int main() {// 创建红黑树实例RedBlackTree<int, int> rbTree;int N;std::cin >> N;getchar();std::string line;for (int i = 0; i < N; i++){std::getline(std::cin, line);std::istringstream iss(line);std::string command;iss >> command;int key;int value;if (command == "insert"){iss >> key >> value;rbTree.insert(key, value);}if (command == "size"){std::cout << rbTree.getSize() << std::endl;}if (command == "at"){iss >> key;int* res = rbTree.at(key);if (res == nullptr){std::cout << "not exist" << std::endl;}else{std::cout << *res << std::endl;}}if (command == "remove"){iss >> key;rbTree.remove(key);}if (command == "print"){if (rbTree.empty()){std::cout << "empty" << std::endl;}else{rbTree.print();}}}return 0;
}

2.1 旋转

1）更换与父结点连接的结点（两步，parent 和 left / right）
2）新的根结点更换右子结点 / 左子节点
3）旧根结点的左子树接上新根结点原来的左子节点 / 右子节点
在这里插入图片描述

// 左旋，旋转就是3个过程void leftRotate(Node* cur) {Node* rSon = cur->right;// if (rSon != nullptr) rSon / cur 为nullptr转不了了rSon->parent = cur->parent;if (!cur->parent) { // 注意先判断是否为空，再使用指针root = rSon;}else if (cur->parent->left == cur) {cur->parent->left = rSon;}else if (cur->parent->right == cur) {cur->parent->right == rSon;}cur->parent = rSon;cur->right = rSon->left;if (rSon->left)rSon->left->parent = cur;rSon->left = cur;}

2.2 插入结点和插入修正

1、插入结点
如果树中已经有相等的key的时候，就不插入了
根据最后结点大小关系确定是插在左子树还是右子树
不管颜色

// 插入节点
void insertNode(const Key& key, const Value& value) {Node* tar = new Node(key, value, Color::Red);Node* cur = root;if (cur == nullptr) { // 加入的第一个节点root = tar;}Node* par = nullptr;while (cur) {par = cur;if (cur->key > tar->key)cur = cur->left;else if (cur->key < tar->key)cur = cur->right;else {// 最后相等的时候，不插入了delete tar;return;}}size++;if (par) {if (par->key > key) {par->left = tar;tar->parent = par;}else {par->right = tar;tar->parent = par;}}insertFix(tar);
}

2、插入修正
只有父结点是红色才需要调整，只有 4种可能的情况（父子两代结点都是红色时一共有 8 种可能（2 * 4），插入结点是左 / 右子树都算一种情况，所以一共4种）
1.1 / 1.2 的区别是插入节点父结点的兄弟结点是红色 / 黑色或不存在
1.1 只要变个颜色就行，就可以继续往上判断
1.2 中插入结点是右子节点的转成左子节点情况操作，然后改变颜色，再旋转
在这里插入图片描述
换成父结点为其父结点的右子树的情况，跟前面两种情况对称，就是转的时候方向相反

// 插入修正
void insertFix(Node* cur) {if (cur->parent && cur->parent->color == Color::Red) {// 只有父结点是红色才需要调整if (cur->parent->parent && cur->parent->parent->left == cur->parent) {// 1.1 & 1.2if (cur->parent->parent->right->color == Color::Red) {// 1.1cur->parent->color = Color::Black;cur->parent->parent->right->color = Color::Black;cur->parent->parent->color = Color::Red;insertFix(cur->parent->parent);}// 1.2else if (cur->parent->parent->right == nullptr || cur->parent->parent->right->color == Color::Black) {if (cur->parent->right == cur) {leftRotate(cur->parent);}cur->parent->color = Color::Black;cur->parent->parent->color = Color::Red;rightRotate(cur->parent->parent);}}else if (cur->parent->parent && cur->parent->parent->right == cur->parent) {// 2.1 && 2.2 if (cur->parent->parent->left->color == Color::Red) {// 2.1cur->parent->color = Color::Black;cur->parent->parent->left->color = Color::Black;cur->parent->parent->color = Color::Red;insertFix(cur->parent->parent);}// 2.2else if (cur->parent->parent->left == nullptr || cur->parent->parent->left->color == Color::Black) {if (cur->parent->right == cur) {leftRotate(cur->parent);}cur->parent->color = Color::Black;cur->parent->parent->color = Color::Red;leftRotate(cur->parent->parent);}}}root->color = Color::Black; // 确保根节点一定是黑色的
}

2.3 删除操作和删除修正

1、删除操作
设置辅助函数是为了处理删除中特有的遇到空节点情况（把那个结点删掉了，空节点都作为黑色处理，因为 Nil 结点是黑色的），也是为了处理哨兵结点（修正的时候没有孩子结点需要用到哨兵整一个叶子节点，统一逻辑）
用新结点替换旧结点时，不考虑孩子节点，因为后面处理不同

// 辅助函数，获取颜色，使空指针变为黑色
Color getColor(Node* cur) {if (cur == nullptr) {return Color::Black;}elsereturn cur->color;
}// 辅助函数，设置颜色
void setColor(Node* cur, Color col) {if (cur == nullptr) {return;}cur->color = col;
}// 辅助函数，断开与哨兵的连接
void disconnectNil() {if (Nil == nullptr) {return;}if (Nil->parent != nullptr) {if (Nil->parent->left == Nil) {Nil->parent->left = nullptr;}else {Nil->parent->right = nullptr;}}
}// 辅助函数，用新结点替换旧结点
void replaceNode(Node* oldNode, Node* newNode) {if (!oldNode->parent) {root = newNode;}else if (oldNode->parent->left == oldNode) {oldNode->parent->left = newNode;newNode->parent = oldNode->parent;}else {oldNode->parent->right = newNode;newNode->parent = oldNode->parent;}// 不考虑孩子节点，因为后面处理不同
}// 辅助函数，寻找以某个节点为根结点的子树中的最小结点
Node* findMin(Node* cur) {while (cur->left) {cur = cur->left;}return cur;
}

删除操作代码
删除的结点要么是有一个子节点的，要么是有两个子节点的，如果没有子节点直接删了就完了

调整的结点就是代替被删除结点的结点

oriColor 是被删除的颜色（不一定就是被删除结点的颜色）

parentPR:
1.对于删除结点同时有左右子节点的，记录替代结点代替之前位置的父结点，为插入Nil结点做准备
2.对于删除结点只有一个子节点的，显然不能记录代替之前的父结点（就是被删除的那个），应该使用删除节点的父结点，为插入Nil结点做准备

如果要删除的节点有两个子节点，那么需要找到它的后继节点（通常是其右子树中的最小节点）或其前驱节点（通常是其左子树中的最大节点），然后将要后继/前驱节点代替那个要删除的结点。需要判断替代节点是否是删除节点的直接孩子，因为这涉及到需不需要把替换节点（新位置需要一系列调整，换了一个结点）和替换替换节点（旧位置同样需要一系列调整，删了一个结点，但是这个删除过程就和只有一个子节点的一致）两部分分开来
如果有删除的结点只有一个子节点，直接用这个子节点代替被删除的结点即可

关于 Nil
Nil节点是黑色： Nil节点默认是黑色的，这是红黑树的基本性质之一。所有的空节点（叶子节点的左右孩子）都被视为黑色节点
根据红黑树的定义，在删除节点时，如果替换的子节点是Nil，它依然保持黑色，从而不破坏黑色节点的数量，也就不会破坏红黑树的性质
为了能顺利插入虚拟 Nil 叶子结点，所以需要时刻保持记录替代节点的父节点

如果调整的结点没有孩子，就无法用相同的逻辑调整，所以需要 Nil 结点

void deleteNode(Node* tar) {Color oriColor = tar->color; // 被删除的颜色（不一定就是被删除结点的颜色）Node* adjust = nullptr; // 调整的结点Node* parentRP = nullptr;// 1.对于删除结点同时有左右子节点的，记录替代结点代替之前位置的父结点，为插入Nil结点做准备// 2.对于删除结点只有一个子节点的，显然不能记录代替之前的父结点（就是被删除的那个），应该使用删除节点的父结点，为插入Nil结点做准备if (!tar->left) {adjust = tar->right;parentRP = tar->parent;//2replaceNode(tar, tar->right);oriColor = getColor(tar->right); // 始终记录替代节点的颜色}else if (!tar->right) {adjust = tar->left;parentRP = tar->parent;//2replaceNode(tar, tar->left);oriColor = getColor(tar->left);}else {Node* nextNode = findMin(tar->right); // 后继节点oriColor = getColor(nextNode);if (nextNode == tar->right) {// 如果替代节点是删除节点的直接右孩子// 不需要把替换节点和替换 替换节点 两部分分开来，一起干就行adjust = nextNode->right; // 替换 替换节点 调整的结点replaceNode(tar, tar->right);// 处理替换结点的子节点nextNode->left = tar->left;if (nextNode->left)nextNode->left->parent = nextNode; // 任何更改肯定是两句话parentRP = nextNode->parent;//1}else if (!tar->parent) // 删除的结点是根结点 {root = tar;tar->parent = nullptr;}else {// 两步：替换节点和替换 替换节点// 替换 替换节点replaceNode(nextNode, nextNode->right);// 替换节点，处理替换结点的子节点replaceNode(tar, nextNode);// 右子节点nextNode->right = tar->right;tar->right->parent = nextNode;// 左子节点nextNode->left = tar->left;tar->left->parent = nextNode;parentRP = nextNode->parent;//1}// 如果替代节点存在，更新其颜色为删除节点的颜色if (nextNode != nullptr) {nextNode->color = tar->color;}// 如果替代节点不存在，将删除节点的颜色赋给origCol变量else {oriColor = tar->color;}}if (oriColor == Color::Black) {if (adjust == nullptr)removeFix(adjust);// Nil节点是黑色： Nil节点默认是黑色的，这是红黑树的基本性质之一。所有的空节点（叶子节点的左右孩子）都被视为黑色节点// 根据红黑树的定义，在删除节点时，如果替换的子节点是Nil，它依然保持黑色，从而不破坏黑色节点的数量，也就不会破坏红黑树的性质// 为了能顺利插入虚拟Nil叶子结点，所以 需要时刻保持记录 替代节点的父节点else {Nil->parent = parentRP;// 如果替代节点的父节点存在，设置其对应的孩子指针为Nil节点if (parentRP != nullptr) {if (parentRP->left == nullptr) {parentRP->left = Nil;}else {parentRP->right = Nil;}}// 进行修复操作removeFix(Nil);// 断开Nil节点与树的连接，因为在红黑树中Nil节点通常是单独存在的disconnectNil();}}// 删除节点delete tar;
}

2、删除修正
x 总是指向一个具有双重黑色的非根结点。（一旦黑红直接涂黑色就完事了）要判断 x 是其父结点 x.p 的左孩子还是右孩子。保持指针 w 指向 x 的兄弟。由于结点 x 是双重黑色的，故 w 不可能是 T.nil，因为否则，从 x.p 至（单黑色）叶子 w 的简单路径上的黑结点个数就会小于从 x.p 到 x 的简单路径上的黑结点数

以 x 为 adjust（需要调整的结点，被删除结点的子节点），w 为其兄弟节点
需要修正的就是双重黑节点的多一重的黑色（代替红色的结点总是合法的）
当w是红色结点时，5个节点的颜色只有一种可能性（图中标白的表示红黑都有可能）

情况1和2是穷尽了兄弟的孩子结点均为黑色的情况，情况3和4加在一起穷尽了兄弟结点的子节点含有红色结点的情况

情况3和情况4是同一种情况（3会转成4），兄弟结点的子节点存在红色结点就可以使两个子树成功出现高度差了，双重黑色自然就解决了

情况1，3，4都是借助兄弟子树的红色结点消除双重黑色结点，情况1转成下面的2，3，4，情况2 / 4 都是最终情况，2是把x上移了，到根结点就结束了；4是直接完成了
在这里插入图片描述

// 删除修正，需要哨兵Nil
// 删除修正四种情况的核心是：兄弟结点的子节点有没有红色结点（有红节点转到父结点的位置上就OK了，如果到根结点还是没有也OK了）？之后是兄弟节点有没有红色节点 /  兄弟结点子节点的红色节点在哪
void removeFix(Node* cur) { // cur就是xwhile (cur != root && getColor(cur) == Color::Black) // 一旦碰到红的就结束了{// 先处理图中所示的左边的情况，右边是对称的if (cur->parent->left == cur) {if (getColor(cur->parent->right) == Color::Red) { // (a)转(b)/(c)/(d)setColor(cur->parent, Color::Red);setColor(cur->parent->right, Color::Black);leftRotate(cur->parent);}else if (getColor(cur->parent->right->left) == Color::Black && getColor(cur->parent->right->right) == Color::Black) {setColor(cur->parent->right, Color::Red);cur = cur->parent;}else if (getColor(cur->parent->right->left) == Color::Red && getColor(cur->parent->right->right) == Color::Black) {setColor(cur->parent->right, Color::Red);setColor(cur->parent->right->left, Color::Black);rightRotate(cur->parent->right);}else {setColor(cur->parent->right, getColor(cur->parent));setColor(cur->parent, Color::Black);setColor(cur->parent->right->right, Color::Black);leftRotate(cur->parent);}}else {Node* bro = cur->parent->left;if (getColor(bro) == Color::Red) { // (a)转(b)/(c)/(d)setColor(cur->parent, Color::Red);setColor(bro, Color::Black);rightRotate(cur->parent);}else if (getColor(bro->left) == Color::Black && getColor(bro->right) == Color::Black) {setColor(bro, Color::Red);cur = cur->parent;}else if (getColor(bro->left) == Color::Red && getColor(bro->right) == Color::Black) {setColor(bro, Color::Red);setColor(bro->left, Color::Black);rightRotate(bro);}else {setColor(bro, getColor(cur->parent));setColor(cur->parent, Color::Black);setColor(bro->right, Color::Black);rightRotate(cur->parent);}}}setColor(cur, Color::Black);
}

红黑树不是完全平衡的二叉树
完全平衡的二叉树（如 AVL 树）要求二叉树的每个节点的左右子树高度差最多为一

3、与标准库的差异

性能和优化
异常处理
模板特化和配置： C++ STL的容器是可配置和可特化的，允许用户提供自定义的比较器、分配器等
迭代器和算法： C++ STL中的容器通常配有迭代器，方便使用STL算法
内存管理： C++ STL标准库中的实现通常使用高效的内存管理技术

RedBlackTree<int> mySet;
// 插入元素
mySet.insert(42);
mySet.insert(63);
mySet.insert(10);
mySet.insert(4);
mySet.insert(30);
mySet.insert(36);

内容在此基础上整理补充：
算法导论总结索引 | 第三部分第十三章：红黑树
https://kamacoder.com/ 手写简单版本STL