寻找存在的路径
题目描述
给定一个包含 n 个节点的无向图中,节点编号从 1 到 n (含 1 和 n )。
你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。
输入描述
第一行包含两个正整数 N 和 M,N 代表节点的个数,M 代表边的个数。
后续 M 行,每行两个正整数 s 和 t,代表从节点 s 与节点 t 之间有一条边。
最后一行包含两个正整数,代表起始节点 source 和目标节点 destination。
输出描述
输出一个整数,代表是否存在从节点 source 到节点 destination 的路径。如果存在,输出 1;否则,输出 0。
输入示例
5 4 1 2 1 3 2 4 3 4 1 4
输出示例
1
提示信息
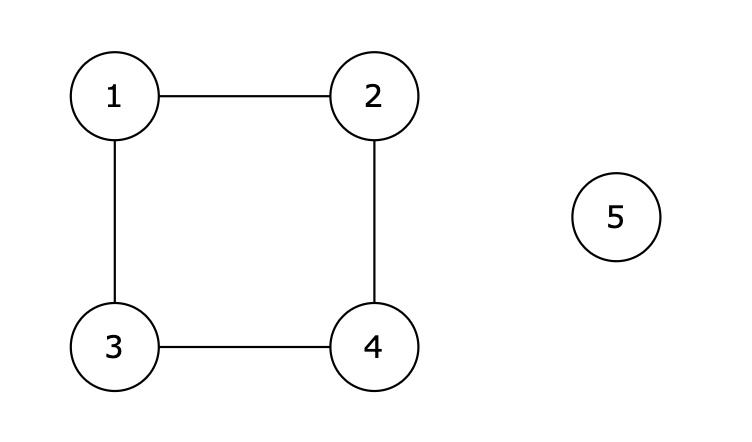
数据范围:
1 <= M, N <= 100。
思路:这道题涉及到了并查集的概念。
那么什么是并查集呢,简单来说并查集的功能就是能够判断两个节点是否在同一个集合里面,并且还能够将两个节点加入同一个集合里面。
实现的方式呢就是使用一个parent数组来保存节点之间的联系,就好像一棵二叉树一样,结点之间是有联系的。
所以一般模板涉及到四个函数,init函数负责初始化每个结点的根节点为自身;find函数负责找到每个结点的根,这里涉及到了路径压缩,也就是可能某个结点距离它的根很远,但是在最后递归找到后,直接将根的值返回,保存在了该结点的parent里面,这样就将路径压缩短了;isSame函数则是判断两个结点的根是否相等;join函数则是将两个结点加入同一个并查集中。
正是因为有了路径压缩,所以一般来说,并查集的时间复杂度是O(logn)到O(1)之间的,刚开始可能是O(logn),但是随着规模越来越大,路径不断被压缩,最终查找的效率就会趋近于O(1)。
所以说回到这道题本身,判断是否有从source到destination的可达路径,那么就将所有边join后,判断source与destination是否具有相同的根即可。如果是,说明是存在这样的一条可达路径;如果不是,则不存在这样一条可达的路径
#include<iostream>
#include<vector>
using namespace std;int n, m;
vector<int> parent(101);
void init(){for(int i = 1; i <= n; i ++){parent[i] = i;//初始化}
}
//找寻根节点
int find(int u){return u == parent[u] ? u : parent[u] = find(parent[u]);//压缩路径
}
//判断两个节点的根节点是否相等
bool isSame(int u, int v){u = find(u);v = find(v);return u == v;
}//存在v->u这样一条边
//将边的两个节点加入并查集
void join(int u, int v){u = find(u);v = find(v);if(u == v) return;parent[v] = u;
}int main(){while(cin >> n >> m){init();int node1, node2, source, destination;for(int i = 0; i < m; i ++){cin >> node1 >> node2;join(node1, node2);}cin >> source >> destination;if(isSame(source, destination)) cout << 1 << endl;else cout << 0 << endl;}
}感谢你的阅读,希望我的文章能够给你帮助,如果有帮助,麻烦点赞加收藏,或者点点关注,非常感谢。
如果有什么问题欢迎评论区讨论!