引言

Mathematica提供了多种工具和函数来实现线性优化,这些工具可以处理从简单的线性规划问题到复杂的多变量优化问题,最近运筹学作业要熟悉线性优化的编程方法,我们就使用mathematica进行:所有运行代码都在文章上面的资源中,免费下载
线性优化问题被定义为目标函数和约束条件都是线性的问题。
如果想快速入门mathematica,那么可以看之前写的博客:
【Mathematica14.0】快速从下载安装到使用-CSDN博客
目录
引言
1.Maximize函数最大值优化
2.Minimize函数最小值优化
3.使用NMinimize/NMaximize进行机器精度优化
4.优化问题主要函数--LinearOptimization
选项选择:
(1)Method
(2)Tolerance
(3)其他
5.内点法/单纯形法/修正单纯形法的区别与使用
(1)线性优化x+y<=1问题
6.对偶
7.处理内点法中的不可行性和无界性
编辑 8."InteriorPoint" 的方法选项
9.线性优化问题应用-L1-范数最小化
10.单纯形法和修正单纯形法算法原理
11.内点法算法原理
1.Maximize函数最大值优化
Maximize函数求解方程的最大值,可以用于线性优化,我们通过函数的说明第三点可以看到,我们加入线性约束,即可对目标函数进行优化求解。

我们对于以下例子进行最大值线性优化求解:

在mathematica中,我们尽量避免使用x1、x2这样的,使用不同字母会好看不少:
转换为mathematica代码如下:

解出最大值为14,x1=4,x2=2,与课本的解一致。
2.Minimize函数最小值优化
我们对目标函数的进行最小值优化可以使用Minimize函数:语法和Maxmize一样


使用mathematica求解得到:

这是mathematica的一个特点,对于小数运算直接返回精确的分数,至于如何直接在计算的步骤中得到小数,在之前的教程中有写:
【Mathematical14.0最新进阶教学】-1-基础计算拓展_mathematica14.0-CSDN博客
3.使用NMinimize/NMaximize进行机器精度优化
那么有的函数可以直接进行小数优化,也就是在最大值最小值优化函数前加上N:
在mathematica中使用效果如下:

4.优化问题主要函数--LinearOptimization
实际上我们在使用线性优化的时候,使用的更多的是LinearOptimization函数。

这个函数返回最小值对应的变量取值。


LinearOptimization函数提供选项:

选项选择:
(1)Method
Method 选项用来指定求解线性优化问题所使用的算法. 可能的值包括 Automatic、"Simplex"、"RevisedSimplex" 、"InteriorPoint"、 "CLP"、"MOSEK" 和 "Gurobi". 默认值是 Automatic,可以根据问题的大小和精度需要从其他方法中自动选择合适的算法:
-
Automatic:这是默认选项,Mathematica 会根据问题的特性自动选择一个合适的算法。这通常是最方便的选择,因为它不需要用户深入了解不同算法的优缺点。
-
"Simplex":单纯形法是一种经典的线性规划算法,由 George Dantzig 在 1947 年提出。它通过迭代的方式沿着可行域的边界移动,逐步改进目标函数的值,直到找到最优解。单纯形法适用于小型到中型规模的问题。
-
"RevisedSimplex":修正单纯形法是对标准单纯形法的一种改进,它使用矩阵分解技术来减少计算量。这种方法在处理大型稀疏线性规划问题时更为高效。
-
"InteriorPoint":内点法是一种现代的线性规划算法,它通过在可行域内部寻找路径来逼近最优解。内点法特别适合解决大规模线性规划问题,因为它们通常具有更好的计算复杂度。
-
"CLP":CLP 是 COIN-OR Linear Programming 的缩写,是一个开源的线性规划求解器。它使用修正单纯形法和内点法来求解线性规划问题。
-
"MOSEK":MOSEK 是一个商业优化软件包,提供了高效的算法来解决线性和二次规划问题,以及混合整数和圆锥优化问题。它支持多种算法,包括内点法和修正单纯形法。
-
"Gurobi":Gurobi 是另一个商业优化软件包,专门用于解决大规模的数学规划问题,包括线性规划、二次规划和混合整数规划问题。它提供了多种算法,包括内点法和分支定界法。
(2)Tolerance
Tolerance 选项可以用来指定收敛容差的大小.
在优化算法中,Tolerance 选项是用来控制算法收敛过程中的容差水平,即决定何时认为算法已经找到了足够接近最优解的解,从而停止迭代。
这个选项对于确定算法的停止准则至关重要。
具体来说,Tolerance 选项的含义是:
【1】数值稳定性:在数值计算中,由于浮点数的表示和运算误差,完全精确的解往往是不可能达到的。因此,需要设定一个容差值,当算法的迭代结果变化小于这个容差时,可以认为已经达到了足够的精度。
【2】收敛判定:在迭代过程中,算法会不断更新解向量。Tolerance 设定了一个阈值,当连续几次迭代之间的解的差异小于这个阈值时,算法将认为已经收敛到一个解,并停止进一步的迭代。
【3】性能权衡:较小的 Tolerance 值意味着算法会追求更高的精度,但这可能会导致计算时间的增加。相反,较大的 Tolerance 值会让算法更快地停止迭代,但得到的解可能不是非常精确。因此,Tolerance 选项提供了一种在计算时间和解的精度之间进行权衡的手段。
在实际应用中,选择合适的 Tolerance 值取决于具体问题的要求。对于某些问题,可能需要非常高精度的解,这时应设置较小的 Tolerance 值;而对于其他问题,如果解的轻微不精确不会对结果产生显著影响,那么可以设置较大的 Tolerance 值以节省计算资源。
(3)其他
当设置为 WorkingPrecision->Automatic 时,精度是从输入参数的精度自动获取的,除非指定的方法仅适用于机器精度,在这种情况下使用机器精度.
可通过LinearOptimization获取解的属性:

5.内点法/单纯形法/修正单纯形法的区别与使用
单纯形法和修正单纯形法通过以下方法解决线性优化问题:
沿着约束条件所定义的多面体边缘移动,从一个顶点到达另一个顶点,以使得目标函数值逐渐减小,直至达到最小值.
Wolfram 语言通过稠密线性代数实现单纯形法和修正单纯形法. 这种实现方法的独特之处在于它有可能解决精确/扩展精度问题. 因此,这些方法对于需要非机器精度结果的小规模问题或者当我们期待得到一个在顶点上的解时更为适用.
笼统地说,线性优化的内点算法是从约束条件定义的多面体的内部依次迭代的. 它们可以非常快地接近问题的解,但是与单纯形法/修正单纯形法不同的是,他们不能精确地找到解.
Wolfram 语言利用机器精度稀疏线性代数执行内点法. 因此,对于大规模机器精度线性优化问题,内点法更为有效,更为适用.
(1)线性优化x+y<=1问题
这个简单的优化问题可以直观得到内点法和单纯形法的不同

首先是内点法的求解:记得一定要在运行前清除变量,不然会报错
LinearOptimization函数默认优化最小值问题,所以我们优化最大值问题可以直接使用对偶形式:也就是取负函数:

内点算法给我们提供了一个位于解集中点的一个解
接下来是改善的单纯形方法:

给出一个边界点,但是两种方法得到的最优化值是一样的
但是在求解大量线性优化问题上,内点法更快:
对于下面的具有 200 个变量的随机稀疏线性优化问题,内点法要快的多,并且产生差不多相同的最优值:

6.对偶


当这两个问题都是可行的时候,(P) 和 (D) 的最优值是相同的,并且下面的补充条件对于原始问题的解x和对偶问题的解λ、v是成立的。
以下面的优化问题为例:

我们首先构建拉格朗日函数,将约束条件融入到目标函数中:

其中, λi≥0 是关联到不等式约束的拉格朗日乘数, νj 是关联到等式约束的拉格朗日乘数。
对偶函数定义为拉格朗日函数的最小值:

最后,构建对偶问题,目标是最大化这个对偶函数:

可通过解的 "DualMaximizer" 属性从 LinearOptimization 获取对偶最大值点
我们求解原问题:

其对偶问题是:

我们使用mathematica求解原问题,并求解对偶问题:

单独运行对偶问题形式验证:
 结果是一样的
结果是一样的

事实证明原始问题和对偶问题给出了相同的目标函数值
用解的属性直接确认原始和对偶目标函数值:

约束条件
![]()
的对偶是
![]()
,这意味着如果约束条件右侧增加一个单位,目标函数将增加两个单位. 这可以通过对约束条件的右侧添加 0.001 的扰动来确认:

用 "ConstraintSensitivity" 属性来查看扰动
![]()
对约束条件
![]()
的影响:

7.处理内点法中的不可行性和无界性
原始-对偶内点法是为可行问题而设计的;对于不可行/无界问题,它是发散的,而在目前的执行过程中,我们很难查明发散是由于不可行性,还是由于无界性.
一种启发式的方法捕捉到了不可行/无界问题,并且发布一个适当的信息:

有时候,该启发式的方法不能肯定地告诉我们一个问题是否是不可行的或者无界的:

使用提示中所建议的 Simplex 单纯形法表明,该问题是无界的:
 8."InteriorPoint" 的方法选项
8."InteriorPoint" 的方法选项
"TreatDenseColumn" 是 "InteriorPoint" 的一个方法选项,它决定对稠密列是否要分别处理. 稠密列指的是具有许多非零元素的约束矩阵的列. 在默认情况下,该方法选项的值为 Automatic,此时分别处理稠密列是分别处理的.
包含稠密列的大型问题通常受益于对稠密列的处理.

9.线性优化问题应用-L1-范数最小化
求解L1最小化问题是可能的:

方法是把系统转换成线性优化问题

定义输入和输出点:

拟合数据:


与用 LeastSquares 获取的拟合相比较:

10.单纯形法和修正单纯形法算法原理
单纯形法和修正单纯形法通过以下方法求解线性优化问题:先在约束条件所定义的多面体的一个顶点构造一个可行解,然后沿着该多面体边,从一个顶点移动到另一个顶点,以使得我们的目标函数值逐渐减小,直至达到最小值.
虽然单纯形法和修正单纯形法的稀疏实现方法在实践上很有效,并且能够保证找到全局最优解,该算法有一个很差的最坏情况下的行为表现:即有可能会建立这样一个线性优化模型,使得单纯形法和修正单纯形法的步骤数目与问题大小呈指数关系.
Wolfram 语言通过稠密线性代数实现单纯形法和修正单纯形法. 这种实现方法的独特之处在于它有可能可以解决精确/扩展精度问题. 因此,这些方法对于需要非机器精度结果的小规模问题更为适用.
这里我们建立一个具有 20 个约束条件和 200 个变量的随机线性优化问题:

下面求解该问题. 通常情况下,如果线性优化问题的变量数目远多于约束数目,修正单纯形法的速度比较快. 反过来,如果约束条件的数目比变量数目多的话,则单纯形法比较快


如果我们只希望得到机器精度的结果,那么问题应该转化成机器精度数字,而且应该使用内点法:

11.内点法算法原理
虽然单纯形法和修正单纯形法平均上看可以非常有效,可是它们最差情况下的行为却很糟糕. 我们有可能会建立一个线性优化模型,其中单纯形法和修正单纯形法的步骤数目随问题大小呈指数增长. 而内点算法收敛所需的步骤数目已经被证明随问题大小呈多项式变化.
此外,Wolfram 语言的单纯形法和修正单纯形法的实现利用稠密线性代数,而它的内点法的实现利用机器精度的稀疏线性代数. 因此对于大规模,机器精度线性优化问题,其内点法更为有效并且更应该使用.
![]()
![]()
、
![]()
、
![]()
. 这个问题可以通过使用障碍函数方法来处理正值约束来求解.
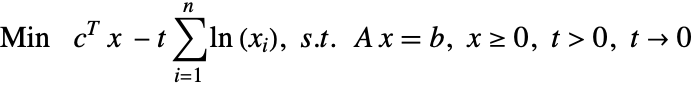
![]()
.

















![onload_tcpdump命令抓包报错Onload stack [7,] already has tcpdump process](https://i-blog.csdnimg.cn/direct/cd3207d121a84c47908d15072a949b01.png)


