文章目录
- week58 FE-GNN
- 摘要
- Abstract
- 一、大数据相关
- 1. 完全分布式zookeeper
- 2. 污水处理过程
- 2.1 污水处理的基本方法
- 2.2 污水处理基本工艺流程
- 二、文献阅读
- 1. 题目
- 2. Abstract
- 3. 文献解读
- 3.1 Introduce
- 3.2 创新点
- 4. 网络框架
- 4.1 特征子空间平坦化
- 4.2 结构化主成分
- 4.3 结论
- 5. 实验过程
- 6.结论
week58 FE-GNN
摘要
本周阅读了题为Feature Expansion for Graph Neural Networks的论文。这项研究讨论了图神经网络(GNN)在图结构数据表示学习中的特征空间问题,特别是在节点分类中。尽管已有方法从优化目标和谱图理论角度探讨了GNN,但其核心特征空间未被充分研究。文章通过分析空间与光谱模型,揭示由于重复聚合导致的线性相关性限制了性能。为此,提出特征子空间扁平化和结构主成分两种策略以扩展特征空间,并根据策略提出了并提出了FE-GNN特征扩展图神经网络。实验表明,新方法有效提升了表现,并保持高效收敛速度和推理时间。
Abstract
This week’s weekly newspaper decodes the paper entitled Feature Expansion for Graph Neural Networks. This study discusses the feature space problem of Graph Neural Networks (GNNs) in learning representations of graph-structured data, particularly in node classification. While existing methods have explored GNNs from the perspectives of optimization objectives and spectral graph theory, the core feature space has not been thoroughly investigated. The paper reveals, through the analysis of spatial and spectral models, that the performance is limited by linear dependencies caused by repeated aggregation. To address this, two strategies are proposed: feature subspace flattening and structural principal components, to expand the feature space. Based on these strategies, a Feature-Expanded GNN (FE-GNN) is introduced. Experiments show that the new method effectively improves performance while maintaining efficient convergence speed and inference time.
一、大数据相关
1. 完全分布式zookeeper
建议按照顺序1、2、3等命名服务器
-
将
/usr/local下所有文件通过xsync传输入slave1和slave2- 若上述方法出现权限相关问题,则在slave1和slave2上重复之前步骤
- 或者将文件压缩之后发送,然后在相应文件夹下解压即可
-
在zkdata创建myid
- 根据zoo.cfg中的server编号赋值
-
按照上述内容配置环境变量
-
创建集群启动脚本,并授权
-
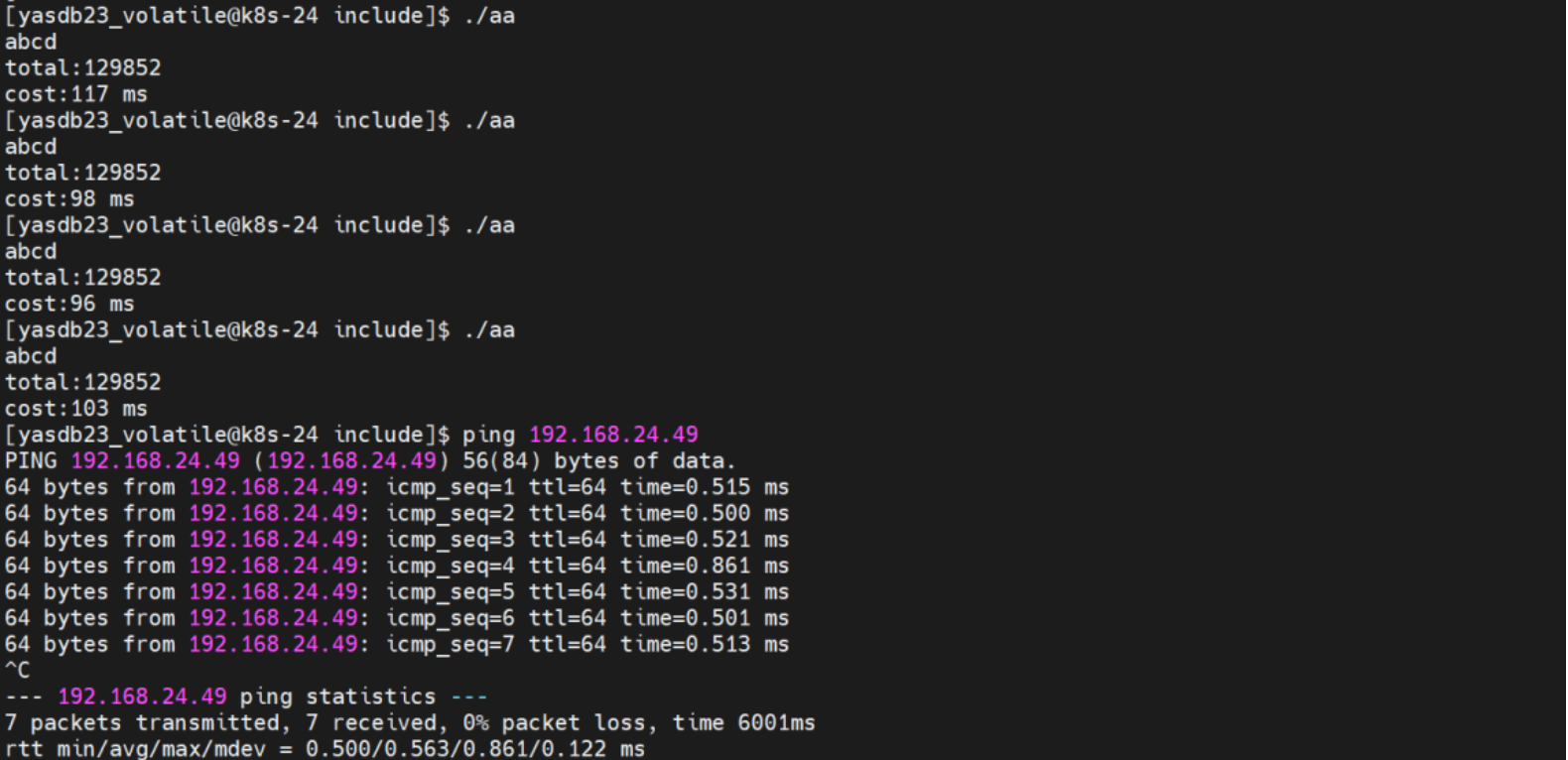
touch zkStart.sh touch zkStop.sh touch zkStatus.sh -
chmod +x zkStart.sh chmod +x zkStop.sh chmod +x zkStatus.sh -
zkStart.sh内容如下 -
#!/bin/bash echo "zookeeper start 11,12,13..." # 更新配置文件,然后启动,配置文件路径按照自身配置填写,以下同理 ssh node11 "source /etc/profile;zkServer.sh start" ssh node12 "source /etc/profile;zkServer.sh start" ssh node13 "source /etc/profile;zkServer.sh start" -
zkStatus.sh内容如下 -
#!/bin/bash echo "zookeeper start 11,12,13..."ssh node11 "source /etc/profile;zkServer.sh status" ssh node12 "source /etc/profile;zkServer.sh status" ssh node13 "source /etc/profile;zkServer.sh status" -
zkStop.sh内容如下 -
#!/bin/bash echo "zookeeper start 11,12,13..."ssh node11 "source /etc/profile;zkServer.sh stop" ssh node12 "source /etc/profile;zkServer.sh stop" ssh node13 "source /etc/profile;zkServer.sh stop"
-
-
最后测试
-
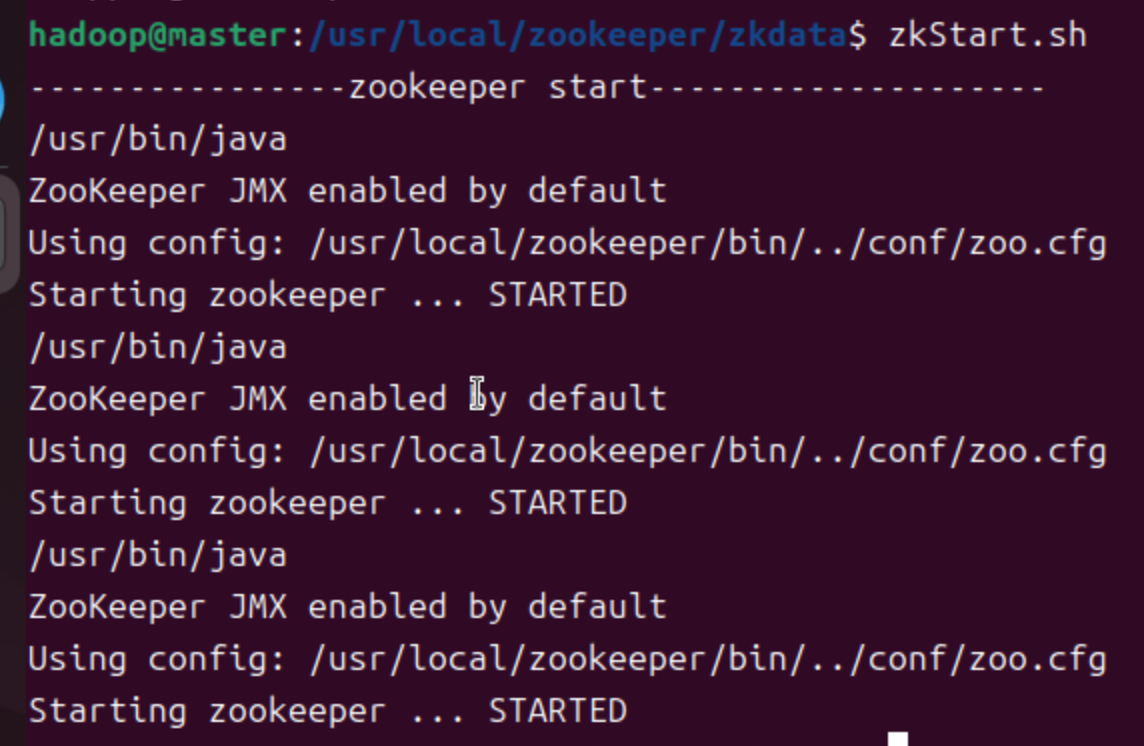
启动
-
查看状态
- tip:注意每个服务器最后一行应当是follower或者leader,若未显示,则检查当前用户是否拥有zookeeper安装目录管理权限,查看
zoo.cfg是否设置监听,IP映射名称是否与ID匹配 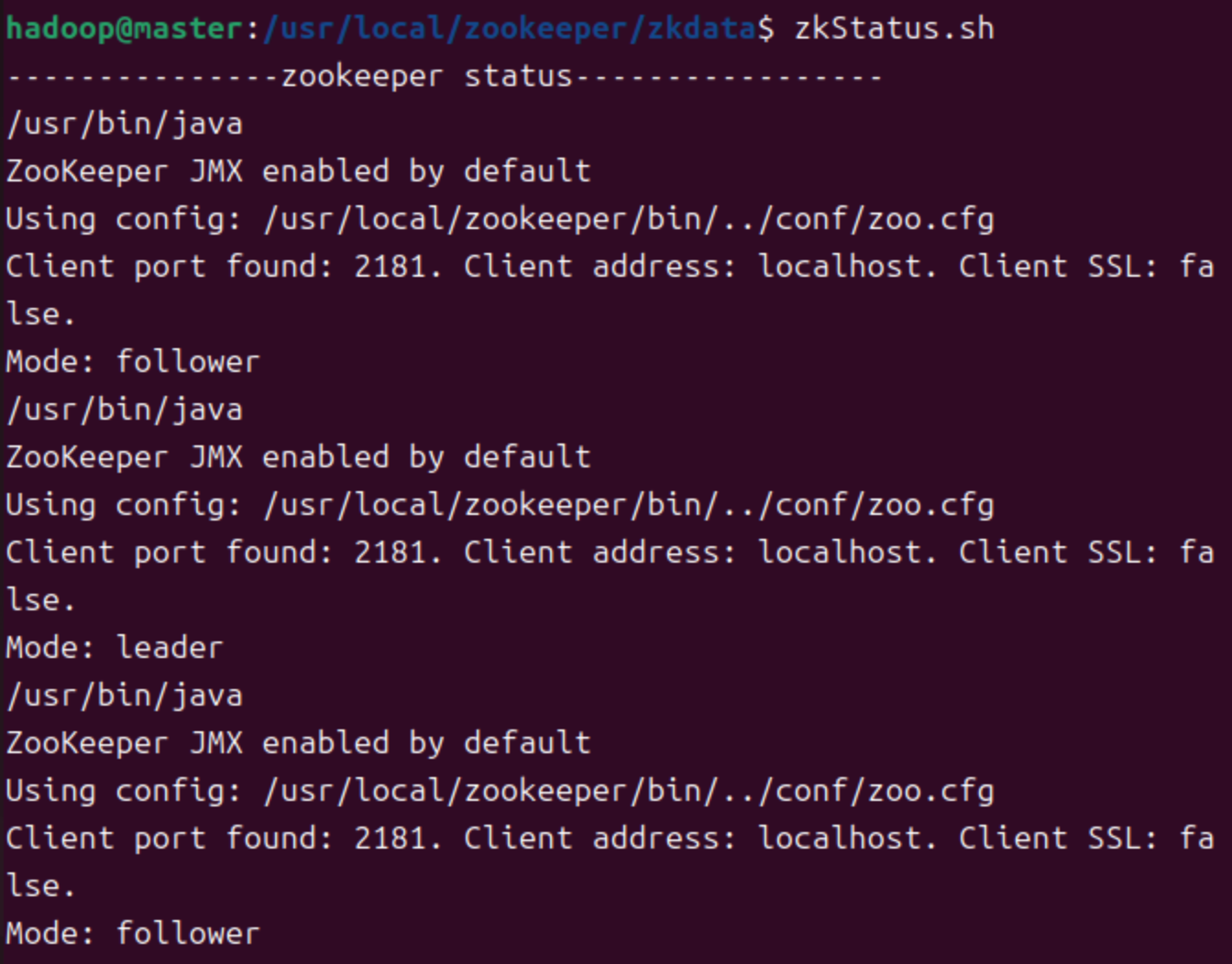
- tip:注意每个服务器最后一行应当是follower或者leader,若未显示,则检查当前用户是否拥有zookeeper安装目录管理权限,查看
-
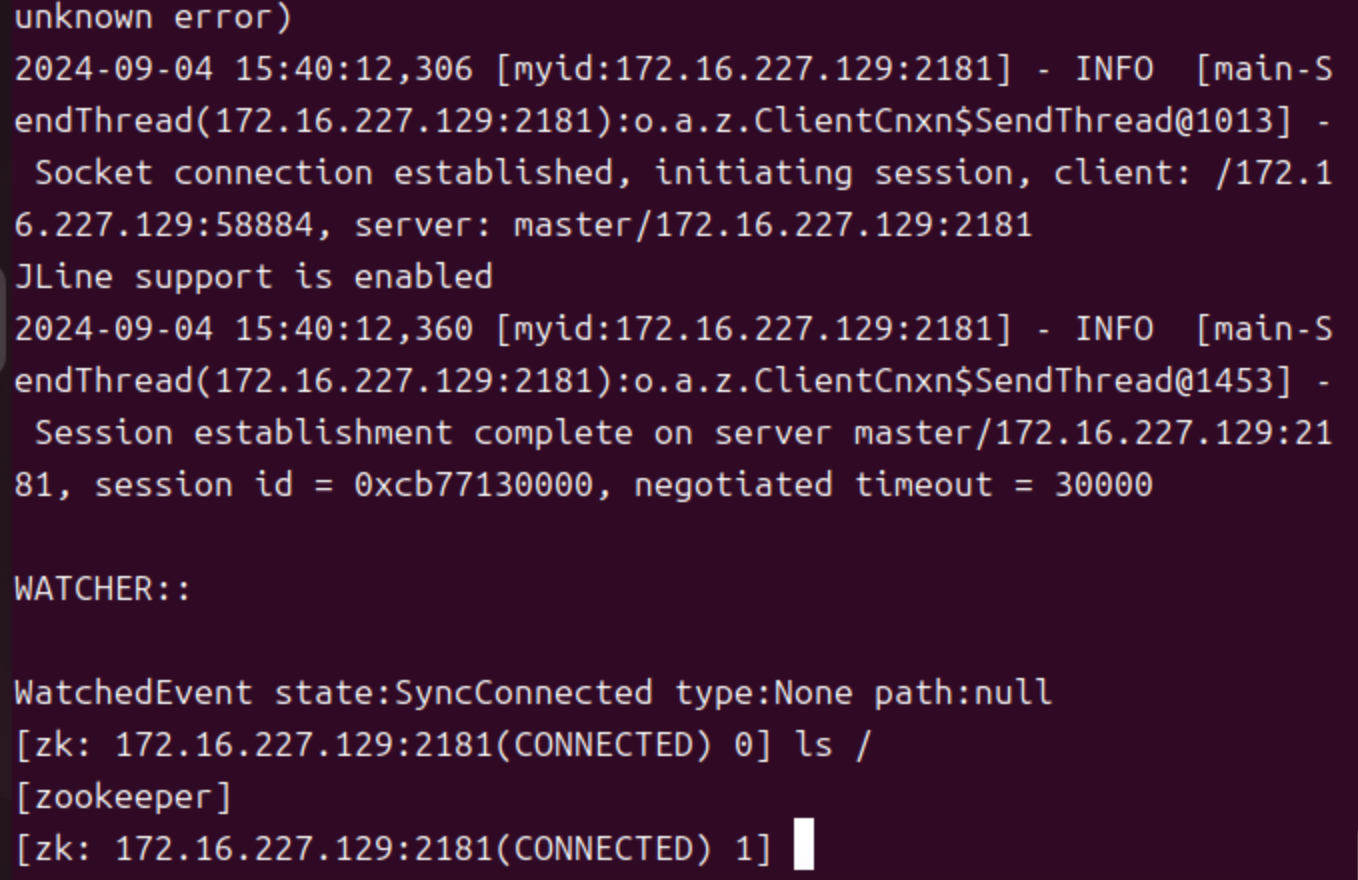
启动客户端
-
2. 污水处理过程
2.1 污水处理的基本方法
- 按处理方法的性质分
物理法:沉淀法、过滤、隔油、气浮、离心分离、磁力分离
化学法:混凝沉淀法、中和法、氧化还原法、化学沉淀法
物理化学法:吸附法、离子交换法、萃取法、吹脱、汽提
生物法:活性污泥法、生物膜法、厌氧工艺、生物脱氮除磷工艺
- 按照水质状况及处理后水的去向分
一级处理:机械处理(预处理阶段)
- 粗格栅及细格栅、沉砂池、初沉池、气浮池、调节池
二级处理:主体工艺为生化处理(主体)
- 活性污泥法、CASS工艺、A2/O工艺、A/O工艺、SBR、氧化沟、水解酸化池。
三级处理:控制富营养化和重新回用
- 高级催化氧化、曝气生物滤池、纤维滤池、活性砂过滤、反渗透、膜处理
中水回用一般都有消毒池:紫外线臭氧消毒池、 二氧化氯消毒池
2.2 污水处理基本工艺流程

- 污水的一级处理
一级处理:机械处理(预处理阶段)
调节池、粗格栅及细格栅、沉砂池、初沉池、气浮池、水解酸化池
- 污水的二级处理
活性污泥法:活性污泥对有机物的降解主要在曝气阶段进行,可分为两个阶段,吸附阶段和稳定阶段。
SBR法:称为序批式活性污泥法是连续式活性污泥法的一种改型,它的反应机制以及污染物质的去除机制和传统活性污泥法基本相同,仅运行操作不一样。
CASS工艺:称为循环活性污泥工艺。在序批式活性污泥法(SBR)的基础上,反应池沿池长方向设计为两部分,前部为生物选择区也称预反应区,后部为主反应区,其主反应区后部安装了可升降的自动撇水装置。整个工艺的曝气、沉淀、排水等过程在同一池子内周期循环运行,省去了常规活性污泥法的二沉池和污泥回流系统;同时可连续进水,间断排水。
A/O工艺:使污水经过厌氧、好氧两个生物处理过程(简称A/O)),达到同时去除BOD、氮和磷的目的。
A 2 ^2 2/O污水处理系统:使污水经过厌氧、缺氧及好氧三个生物处理过程(简称A2/O)),达到同时去除BOD、氮和磷的目的。
氧化沟:是一种改良的活性污泥法,其曝气池呈封闭的沟渠形,污水和活性污泥混合液在其中循环流动,因此被称为“氧化沟”,又称‘‘环形曝气池”。
AB工艺:污水由排水系统经格栅和沉砂池直接进入A 段,该段为吸附段,负荷较高,泥龄短, 水力停留时间很短, 约为30min, 有利于增殖速度较快的微生物生长繁殖。污水从A段流出后进入B段,B段为生物氧化段,属于传统活性污泥法,一般在较低负荷下运行,停留时间约为2~6h,泥龄较长,为15~20d。
- 污水的三级处理
经二级生物处理后,其出水一般含有:BOD30mg/L左右,COD60mg/L左右,NH315-25mg/L,P3-8mg/L,SS30mg/L左右,以及细菌、重金属等,必须经过处理,否则易导致水体富营养化,并对鱼类,农作物、淡水水质及处理成本等带来影响。
三级处理的方法包括:砂滤、混凝、微滤、反渗透、电渗析、离子交换、消毒、活性炭吸附、脱氮除磷等。

二、文献阅读
1. 题目
标题:Feature Expansion for Graph Neural Networks
作者:Jiaqi Sun, Lin Zhang, Guangyi Chen, Peng Xu, Kun Zhang, Yujiu Yang
发布:ICML2023
链接:https://dl.acm.org/doi/10.5555/3618408.3619785
代码连接:https://github.com/sajqavril/Feature-Extension-Graph-Neural-Networks.git
2. Abstract
图神经网络旨在学习图结构数据的表示,并表现出令人印象深刻的性能,特别是在节点分类方面。近年来,许多方法从优化目标和谱图理论的角度研究了gnn的表示。然而,在图神经网络中,主导表征学习的特征空间尚未得到系统的研究。在本文中,建议通过分析空间和光谱模型的特征空间来填补这一空白。将图神经网络分解为确定的特征空间和可训练的权值,为利用矩阵空间分析明确地研究特征空间提供了方便。特别是,从理论上发现,由于重复聚集,特征空间倾向于线性相关。在这种情况下,特征空间受到现有模型中共享权值表示不佳或节点属性维数有限的限制,导致性能不佳。基于这些发现,提出1)特征子空间扁平化和2)结构主成分来扩展特征空间。大量的实验验证了提出的更全面的特征空间的有效性,与基线的推理时间相当,并证明了其高效的收敛能力。
本文研究图神经网络(GNN)在学习图结构数据表示中的特征空间问题,尤其是在节点分类任务中表现出色的背景下。尽管已有不少方法从优化目标和谱图理论角度探讨了GNN的表现,但其核心特征空间的研究仍不充分。为此,文章提出通过分析空间与光谱模型来探索这一领域,并将GNN分解为确定性特征空间及可训练权重两部分,便于采用矩阵空间方法深入研究。研究揭示,由于重复聚合操作,特征空间易呈现线性相关性,进而因共享权重或有限维度属性导致性能受限。基于此发现,作者提出了特征子空间扁平化和结构主成分两种策略以扩展特征空间。实验结果表明,所提方案不仅有效提升了表现,还保持了高效的收敛速度与推理时间,证明了新方法的有效性和实用性。
3. 文献解读
3.1 Introduce
首先抽象出gnn的线性近似。然后,在线性逼近中分解带参数和不带参数的GNN分量,其中带参数的GNN分量被认为是由节点属性和图结构(如邻接矩阵或拉普拉斯矩阵)构建的特征空间,带参数的GNN分量表示可学习的参数,用于对特征进行重加权。
利用分解的便捷性,对当前模型的特征空间进行检测。由于gnn被期望拟合任意目标,更全面的特征空间反映了更好的可表征性,而无需对数据分布进行任何假设。然而,从理论上发现,当前gnn的特征子空间受到权重共享机制和节点属性维数的限制。为了缓解上述限制并扩展特征空间,分别提出了1)特征子空间平坦化和2)结构主成分。具体而言,前者独立地重新加权所有特征子空间以获得完全表达的表示。后者将图结构矩阵的主成分作为原始特征空间的“补充”。需要强调的是,方案没有对图和目标做任何假设,具有很好的通用性。在同性和异性数据集上进行了广泛的实验,以证明该建议的优越性。
3.2 创新点
主要贡献如下
- 从表示学习开始,首次对图结构数据中形成的特征空间进行了研究。基于这一观点,研究了典型的空间gnn和频谱gnn,并识别了现有gnn由于有界特征空间而存在的两个问题。
- 提出两种改进方法:
- 特征子空间扁平化
- 结构主成分扩展整个特征空间。
- 在亲同性和亲异性数据集上进行了大量的实验,建议取得了显著的改进,例如在亲异性图上平均准确率提高了32%。
4. 网络框架
4.1 特征子空间平坦化
对于第一个问题,鼓励每个特征子空间在模型中相互独立地表示,并分别对它们进行加权。在给出支持证据之前,在图2中提供了这个修改的说明。这个建议的好处如下。
T h e o r e m 4.1 假定 Φ a , Φ b ∈ R n × d 为两个线性相关的特征子空间, 例如有 W a ∈ R d × d 使得 Φ a W a = Φ b ,且矩阵 B ∈ R d × c , c < < d 。 若 B 可由 Φ a 表示,如 Φ a W B = B ,则使用两个独立的子空间 Φ a 和 Φ b , 即 Φ a W a + Φ b W b = B ,该最优化方式比参数共享更容易 \begin{aligned} &\mathbf {Theorem 4.1}\quad 假定\Phi_a,\Phi_b\in \mathbf R^{n\times d}为两个线性相关的特征子空间,\\ &例如有W_a\in\mathbf R^{d\times d}使得\Phi_aW_a=\Phi_b,且矩阵B\in \mathsf{R}^{d\times c},c<<d。\\ &若B可由\Phi_a表示,如\Phi_aW_B=B,则使用两个独立的子空间\Phi_a和\Phi_b,\\ &即\Phi_aW_a+\Phi_bW_b=B,该最优化方式比参数共享更容易 \end{aligned} Theorem4.1假定Φa,Φb∈Rn×d为两个线性相关的特征子空间,例如有Wa∈Rd×d使得ΦaWa=Φb,且矩阵B∈Rd×c,c<<d。若B可由Φa表示,如ΦaWB=B,则使用两个独立的子空间Φa和Φb,即ΦaWa+ΦbWb=B,该最优化方式比参数共享更容易
由该定理可知,当特征子空间趋于线性相关时,特征子空间平坦化比权值共享方法更有效。
4.2 结构化主成分
考虑第二个问题,即节点属性的维度是有限的。建议通过引入其他特征子空间来扩展整个特征空间。
考虑了两个标准。
- 引入的特征子空间应该与已有的特征子空间高度不相关,否则根据上一节的分析,在这种情况下,它可能与之前提出的修改不一样。
- 引入的子空间维数不能太大,否则可能包含噪声,也会增加计算量。

因此,对于图结构数据,有两种数据矩阵,即节点属性和图结构矩阵,在大多数GNN模型中,节点属性已经被明确地利用为特征子空间之一,如表1所示。相反,结构矩阵只能与节点属性结合使用。在这些条件下,提出利用结构矩阵的截断SVD,称为结构主成分作为修正2来构造扩展子空间。它自然地提供了正交的子空间,截断的形式限制了矩阵的维数。因此,满足两个条件。具体来说,提取图结构的低维信息,得到图结构的主成分:
S = Q ~ V ~ , A ^ = Q V R T (10) S=\tilde Q\tilde V,\hat A=QVR^T\tag{10} S=Q~V~,A^=QVRT(10)
T h e o r e m 4.2 设节点属性的维数远小于节点数,即 d < < n , X ∈ R n × d , 且有一个由 z 截断的 L 的 S V D ,满足 ∣ ∣ U z S Z − L ∣ ∣ 2 < ϵ , 其中 ϵ 时一个足够小的常数。 则线性系统 ( Φ k , U z S z ) W B ′ 比线性系统 Φ k W B = B 更能达到一个更小的误差 \begin{aligned} &\mathbf {Theorem\ 4.2}\quad 设节点属性的维数远小于节点数,即d<<n,X\in\mathbb R^{n\times d},\\ &且有一个由z截断的L的SVD,满足||U_zS_Z-L||_2<\epsilon,其中\epsilon时一个足够小的常数。\\ &则线性系统(\Phi_k,U_zS_z)W'_B比线性系统\Phi_kW_B=B更能达到一个更小的误差 \end{aligned} Theorem 4.2设节点属性的维数远小于节点数,即d<<n,X∈Rn×d,且有一个由z截断的L的SVD,满足∣∣UzSZ−L∣∣2<ϵ,其中ϵ时一个足够小的常数。则线性系统(Φk,UzSz)WB′比线性系统ΦkWB=B更能达到一个更小的误差
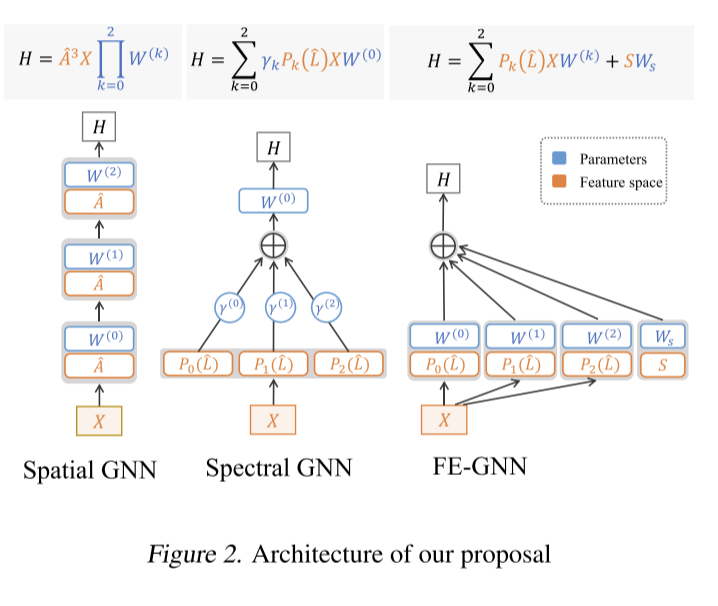
到目前为止,已经引入了两个修改,它们共同贡献了一个新的GNN模型,称为特征扩展图神经网络(FE-GNN)。如图2所示,公式如下:
H = ∑ k = 0 K P k ( L ^ ) X W ( k ) + S W s (11) H=\sum^K_{k=0}P_k(\hat L)XW^{(k)}+SW_s\tag{11} H=k=0∑KPk(L^)XW(k)+SWs(11)
它通过两种方式构造特征空间。第一部分继承了基于多项式的gnn,利用结构矩阵Pk(L)与节点属性x的多项式相乘,利用结构矩阵的主成分形成另一个特征子空间s。此外,FE-GNN使用独立的参数矩阵W(k)和W对每个特征子空间进行重权,提供灵活的重权。
它通过两种方式构造特征空间。第一部分继承了基于多项式的gnn,利用结构矩阵Pk(L)与节点属性x的多项式相乘,利用结构矩阵的主成分形成另一个特征子空间s。此外,FE-GNN使用独立的参数矩阵W(k)和W对每个特征子空间进行重权,提供灵活的重权。
特别是, Φ k \Phi_k Φk和S特征空间可能具有不平衡的尺度,导致重加权效果不佳。因此,增加了一种逐列归一化,以确保每个特征子空间的每一列对整个特征空间的贡献相等。最后,为了更好地验证特征空间视图的重要性,实现是纯线性的,除了交叉熵损失之外,没有任何深层的技巧,如激活函数或dropout,而服从基线的原始实现,并且保留了它们的非线性。
4.3 结论
分析和建议对节点属性的分布,图结构,甚至它们之间的关系做了很少的假设。由于特征空间的观点并不是专门针对图结构数据或gnn提出的分析方法,因此研究更加一般化,跳出了其他观点的限制。例如,图去噪和谱图理论视图都忽略了节点属性的性质,这是第二个建议的关键,而是关注结构矩阵的变换。
在提出的方法中,第一种修改是使特征子空间平坦化,提高了每个特征子空间的有效性,但由于没有共享的参数矩阵,因此参数的数量必须更高。在实验中,惊讶地发现与基线相比,训练时间成本相对较低。此外,第二种修改可以被误解为结构信息的任意添加。考虑到这一点,将使用其他信息提取方法进行额外的实验。此外,在方法中,可以将聚合过程抽象为预处理,进一步加快训练过程。把这个作为未来的工作;在实验中,为了公平的比较,在每次训练期间计算聚合。
最后,值得注意的是,对于非线性GNN采用线性近似的原因如下:1)它允许更深入地观察GNN模型,2)线性化在一般机器学习和深度学习分析的理论分析中是一种相当正常的设置,因为非线性很难提供严格的论证, 3)提出的模型完全符合线性的分析观点。
5. 实验过程
数据集:
在亲同性数据集上进行实验,即Cora、CiteSeer、PubMed、Computers和Photo (Yang et al., 2016;Shchur等人,2018),以及het-erophilic Chameleon, Squirrel, and Actor(Rozemberczki等人,2021;Pei et al., 2020)。其中Chameleon和Squirrel是两个案例,它们都有问题2,即节点属性维度有限,没有同族假设可以使用。
基线:
比较了一系列最先进的GNN方法。对于空间gnn,有GCN (Kipf & Welling, 2017)、GAT (Velickovic等人,2018)、GraphSAGE (Hamilton等人,2017)、GCNII (Chen等人,2020)和APPNP (Klicpera等人,2019),其中MLP是一个特例。对于谱域方法,采用ChebyNet (Defferrard等人,2016)、GPRGNN (Chien等人,2021)和BernNet (He等人,2021)。还介绍了最近的统一模型ada - ugn (Ma等人,2021)和GNN-LF/HF (Zhu等人,2021)。FE-GNN使用Chebyshev多项式或单多项式来构建特征空间,将相应的版本分别称为FEGNN ©和FE-GNN (M)。
节点分类:
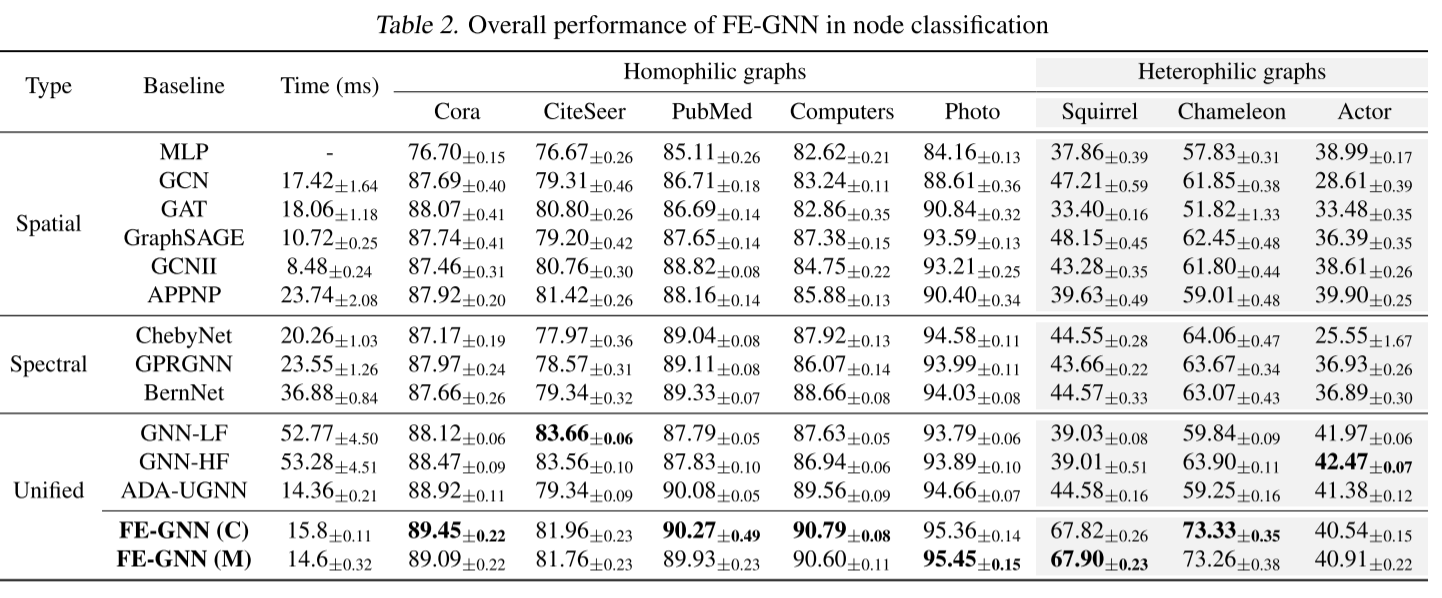
以随机的60%/20%/20%分割对节点分类任务进行测试,并在表2中总结了100次运行的结果,报告了95%置信区间的平均准确率。观察到FE-GNN在同亲图上几乎具有最好的性能。特别是,与目前统一空间和光谱域目标的SoTA方法ada - ugn (Ma et al., 2021)相比,FE-GNN在5个同态图数据集上平均提高了1.1%的精度。将Citeseer上GNN-LF/HF的优越性能归因于其复杂的超参数调谐,其中可以找到更细粒度的参数约束(未来工作),此外,FE-GNN在三个异亲图数据集上的平均性能比GCN基线提高了32.0%。值得强调的是,FE-GNN在两个数据集上的巨大优势,它们完全符合对第二种修改的假设,即节点属性的异亲性和有限维度。消融研究的结果也与此一致。
消融实验:
Q:特征扁平化是否有效?
A:是的。
在表3中,将提议与保留主成分的权重共享(WS)实例进行比较。结果表明,随着特征子空间数量的增加,平坦化特征子空间的性能总是更好
Q:什么时候结构主成分起作用?
A:关于有限节点属性和异亲情况。
在5个数据集上评估了FE-GNN在3种不同特征空间结构下的性能: w / o S , w / o P k ( L ^ ) X k = 0 , a n d w / o P k ( L ^ ) X k > 0 w/o\ S,w/o\ P_k(\hat L)X_{k=0},and\ w/o\ P_k(\hat L)X_{k>0} w/o S,w/o Pk(L^)Xk=0,and w/o Pk(L^)Xk>0,这3种不同的特征空间结构分别表示无图结构、无注释属性和无两者结合的特征空间结构。在表5的消融结果中,发现w/o S在同亲图上表现良好,但在异亲图(节点属性维数有限)上表现不佳,而其他两种方法表现相反。同时,w/ S极大地改善了有界情况,这些结果证实了提出结构主成分的初衷。此外,在附录B.3中提供了其他变体,其中包括结构信息,作为在第4.3节中讨论的扩展,并在附录A.8中提供了逐行规范化,其中建议相对有效。
有效性检验:
最后,检验了建议的效率,包括训练时间成本和截断的奇异值分解时间。在表2中,收集了每种方法的每个epoch的训练时间(ms),这表明FE-GNN的行为与其他基线的时间成本相当,尽管它从独立的特征表达式中承担了更多的计算成本。请注意,报告的时间包括图传播以进行公平比较,尽管FE-GNN可以通过以预处理方式构建特征空间来进一步减少它。在图5中,比较了所有方法的收敛时间,可以看到FE-GNN消耗的训练epoch数最少,而准确率最高,这正好揭示了定理4.1中更容易优化的结论。在表4中,给出了训练时间和SVD时间(作为预处理),从中发现SVD时间占总训练时间的比例小于10%,证实了其适用性。
6.结论
在本文中,提供了特征空间视图来分析gnn,将特征空间与参数分离。同时,对gnn现有的特征空间进行了理论分析,并总结了两个问题。针对这些问题,提出了1)特征子空间平坦化和2)结构主成分。大量的实验结果验证了其优越性。
非线性的情况不包括在我们的工作中,将在未来的工作中考虑。此外,子空间之间的相关性应在线性相关性质之外进行更仔细的研究;从某种意义上说,通过引入合理的约束,可以进一步减小参数。最后,需要为今后的工作发现更多的特征空间构建方法。