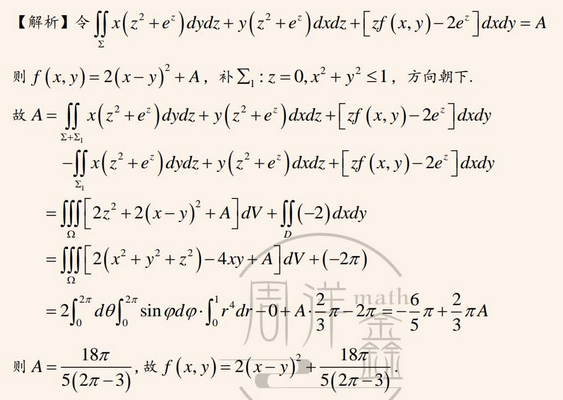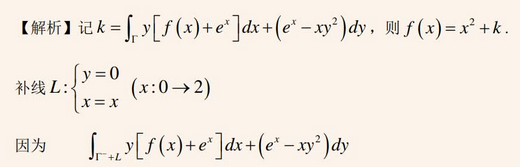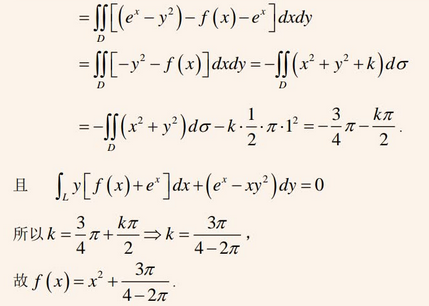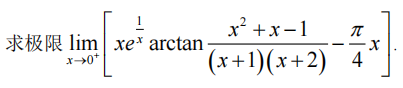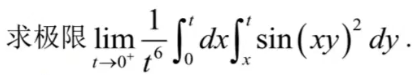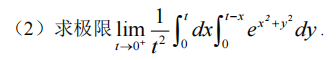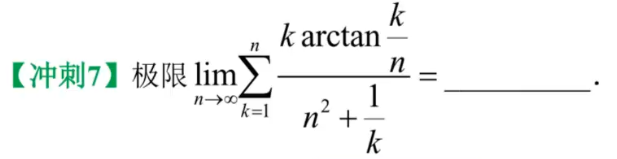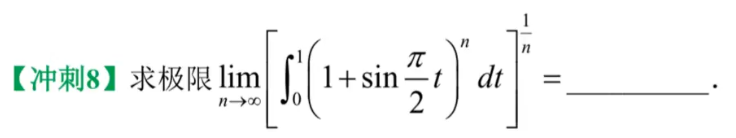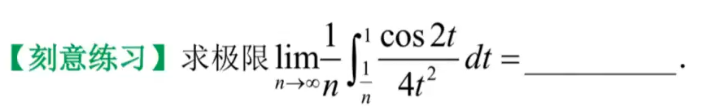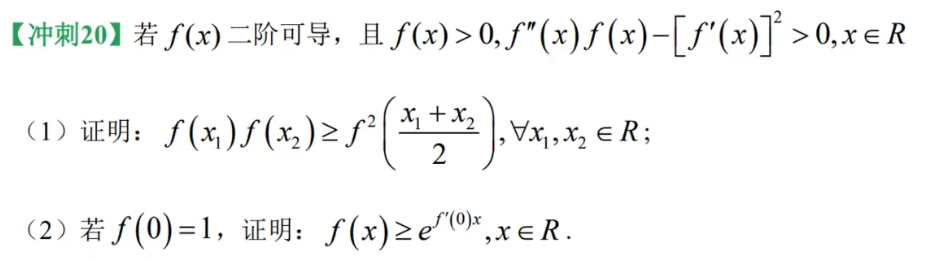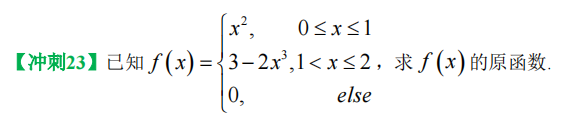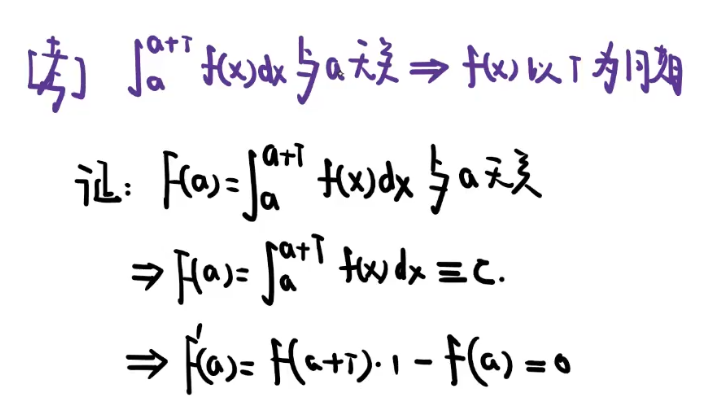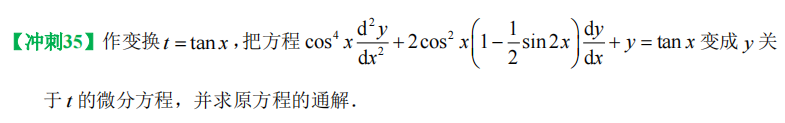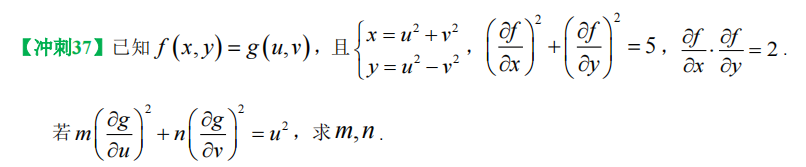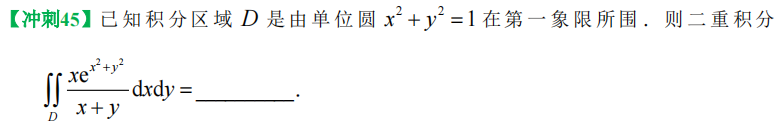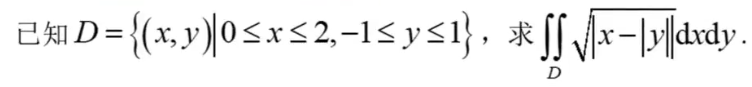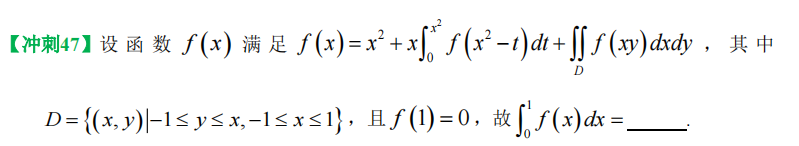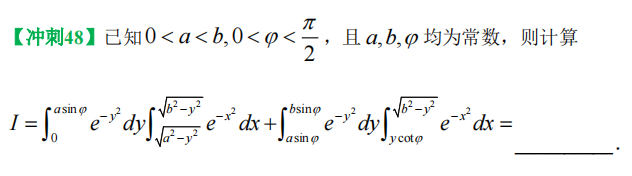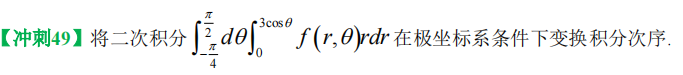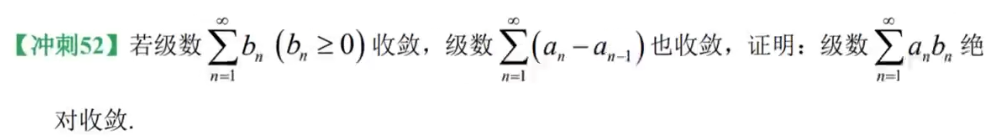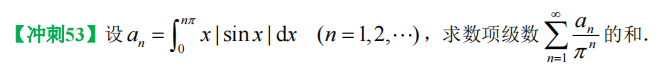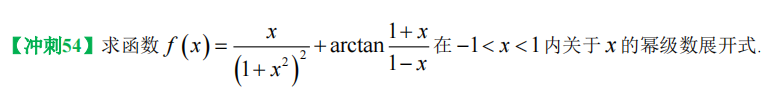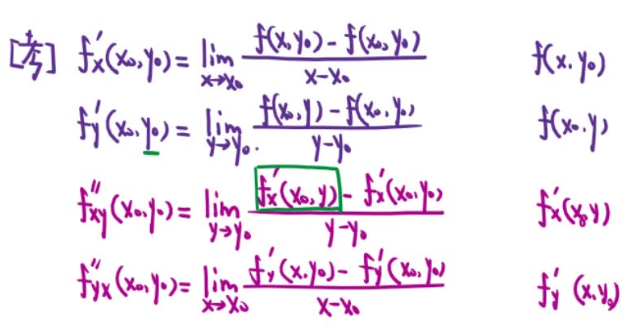自用笔记整理复习。
内容来自2023周洋鑫冲刺班。
加油ヾ(◍°∇°◍)ノ゙
1、函数极限计算
【加项减项】

☆ 二次积分求极限


【分母与面积同阶】—— 走二重积分中值定理
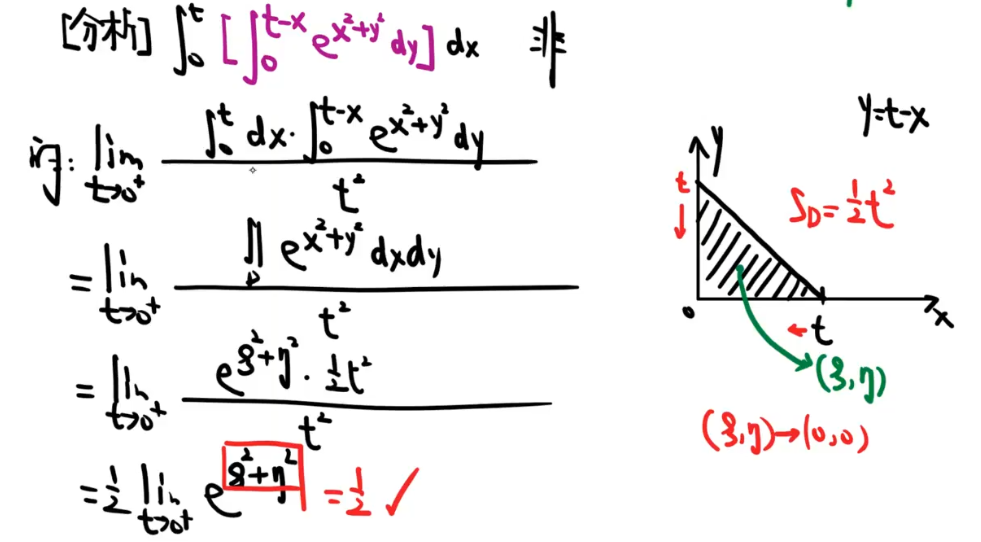
☆ 中值点的包装
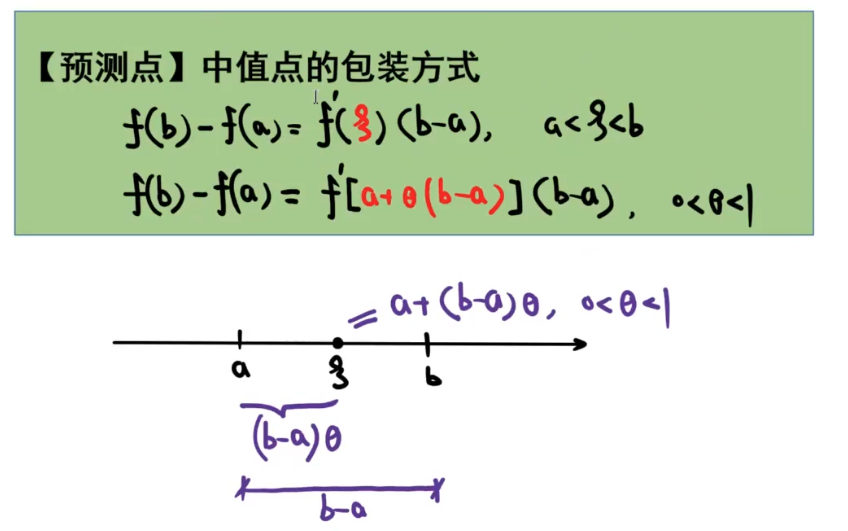

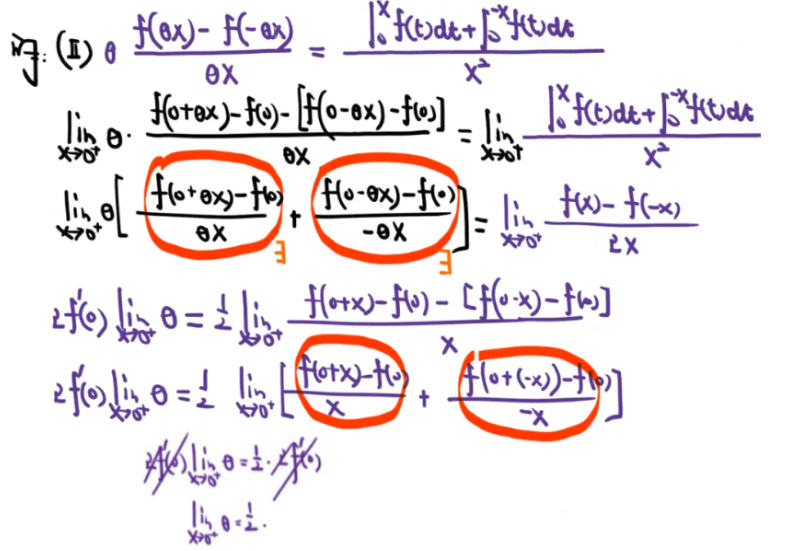

学思想 —— 别忘了可以洛必达

2、数列极限

【压缩映射原理】
高数 | 【数列】递推型数列 与 极限_西皮呦的博客-CSDN博客

【注意 凑不成可爱因子 考虑放缩】
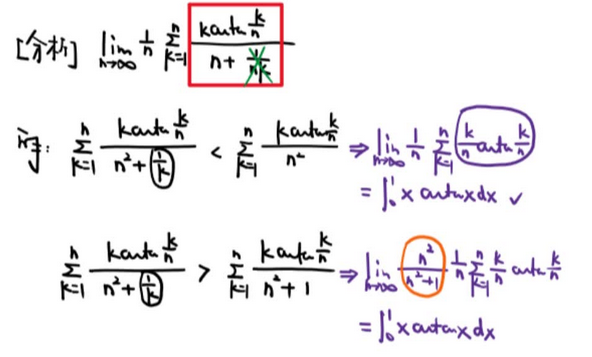
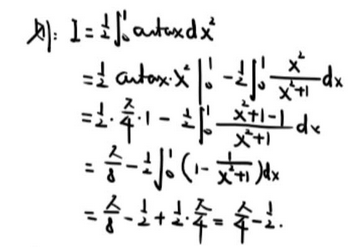
学思想 —— 【连续不行 定积分不行 单调有界不行 只剩夹逼 学 放缩】
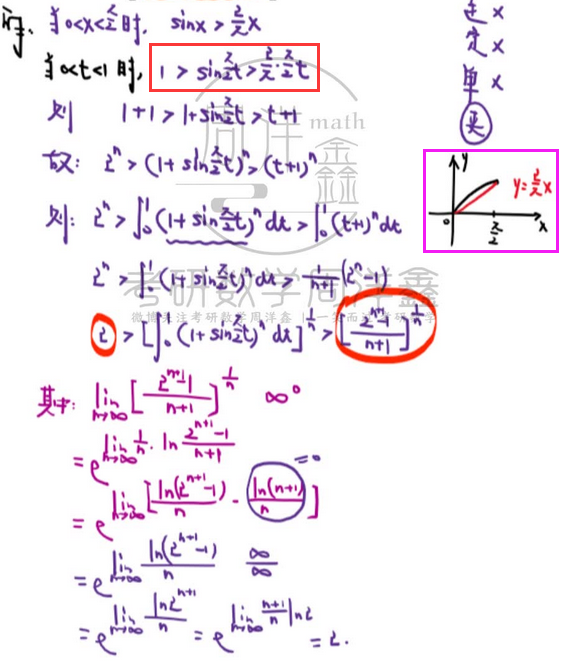
【数列积分极限、利用 泰勒公式 —— 放缩】

【比较简单】
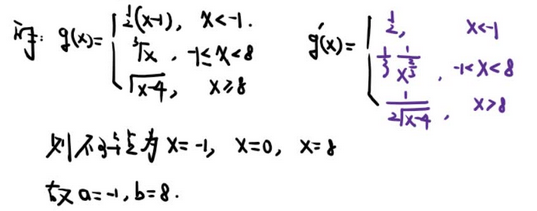
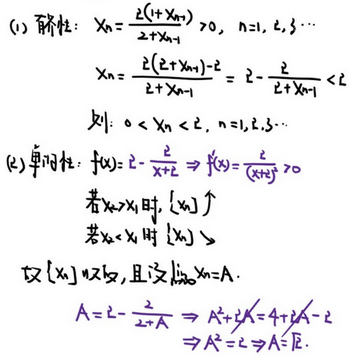
【2016 数一 数列极限】



3、连续与间断

【分母不为0、无定义点、分段函数分段点】
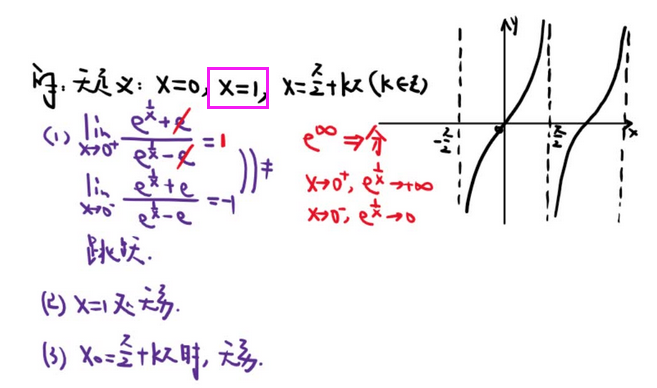
4、导数定义及计算
☆ 回顾 参数方程反函数二阶导公式

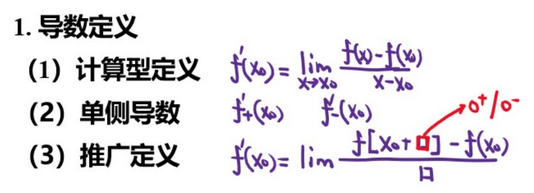

☆ 分段函数分段点导数

高数 | 导数极限定理、分段点求导能不能用公式?导数和导数的极限?_西皮呦的博客-CSDN博客_导数极限定理
【抽象函数极限】

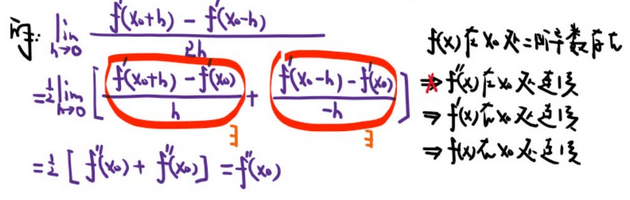
☆ 不在零点处的泰勒公式展开 —— 高阶导


5、极值点、拐点

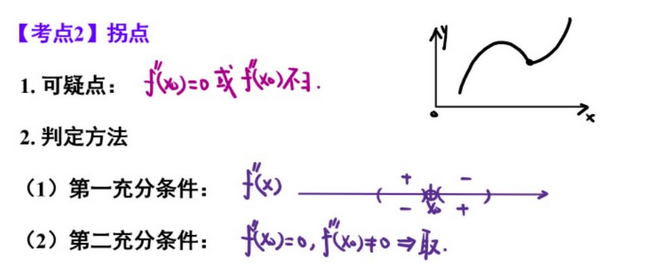
【注!二阶导不知道是否连续,不能推出 该点二阶导为0】
【解析】B —— 不取拐点 二阶导不知道是否连续,不能推出 该点二阶导为0
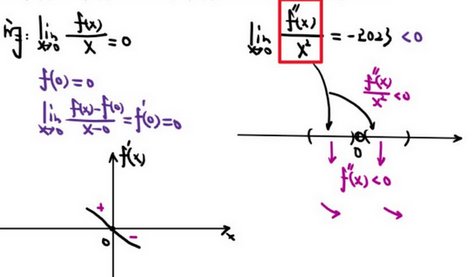
6、方程根、函数零点问题

【再看一下思路就行 感觉很简单。】
7、不等式证明

【思维方式 —— 注意取对数的使用】
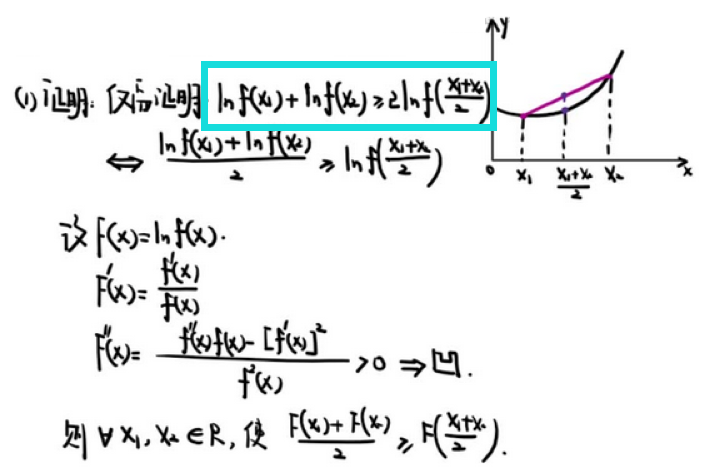
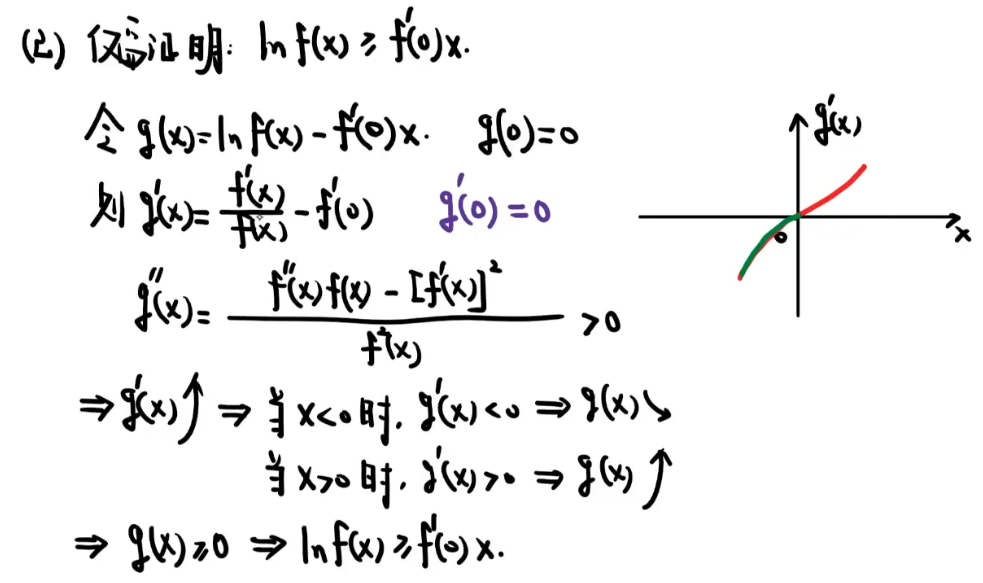
8、中值定理
泰勒公式:
第一种形式:皮亚诺余项 —— 展开到几阶,几阶存在
第二种形式:拉格朗日余项 —— n阶导数,在区间内有定义
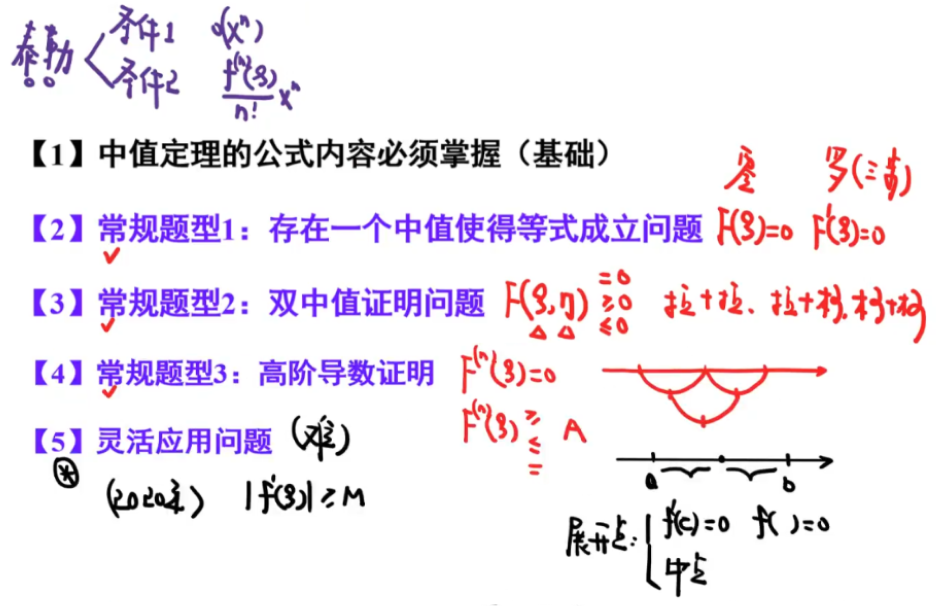
【构造函数 一阶线性】
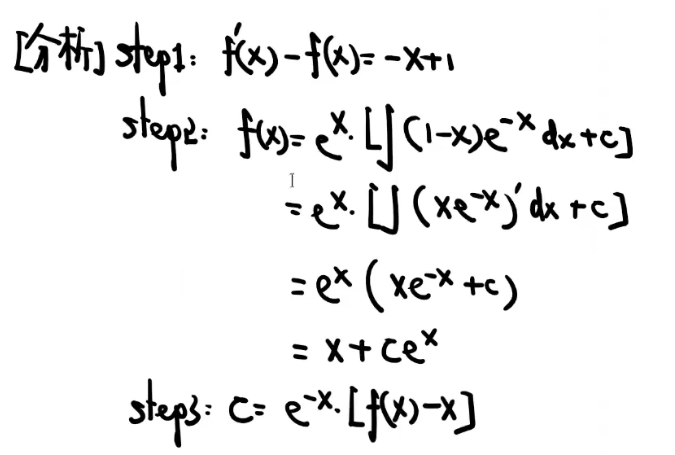
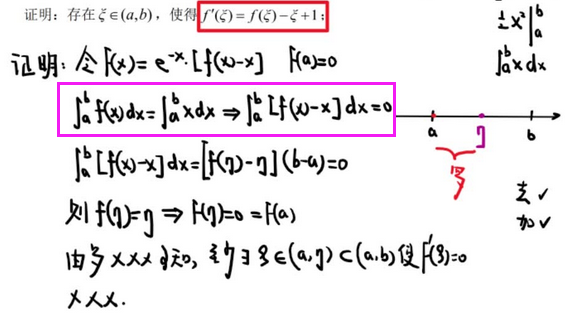
【泰勒 泰勒 泰勒】
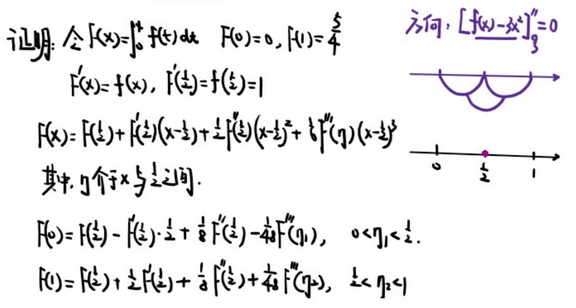

9、积分学定义、性质

【分段函数不定积分 注意连续调整常数 注意 f 为0 处 分段】
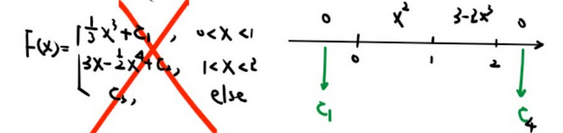
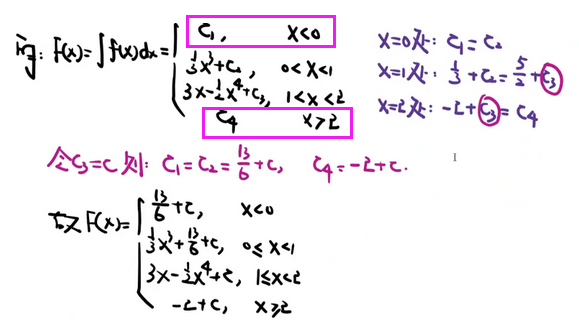
【积不出来 用 牛犇爸】
☆ 含有变限函数的等式
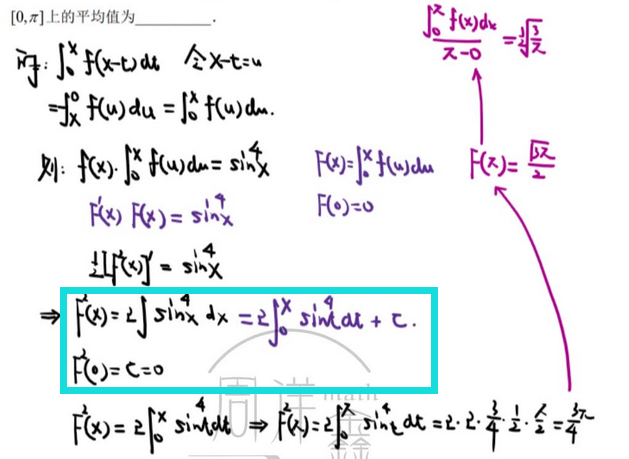

☆ 积分限带a的积分 与 a 无关
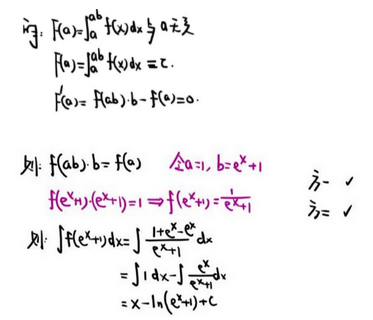
☆ 10、反常积分


判敛方法总结(不会方法的先看这个)_哔哩哔哩_bilibili
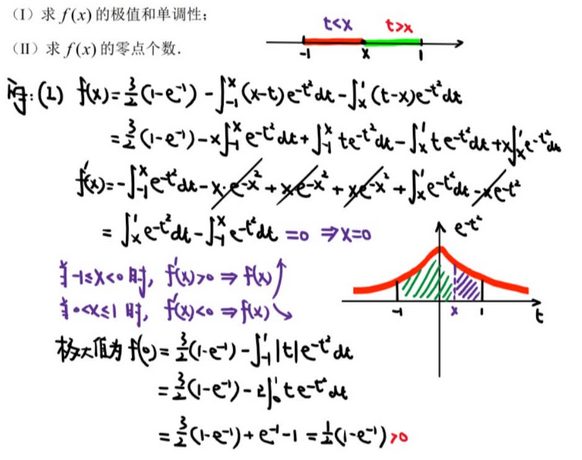
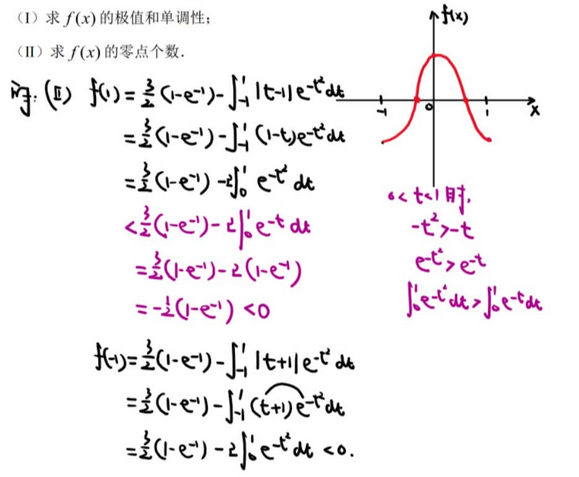
11、定积分几何应用

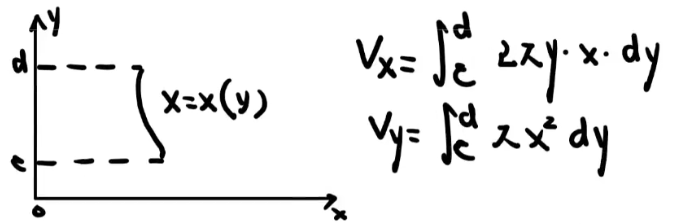

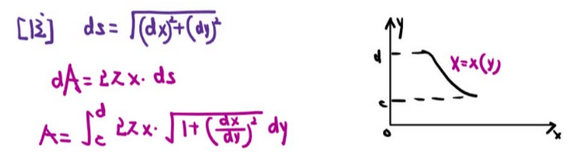
【转化变量 构建微分方程 再看一下思路 感觉挺简单的】

【第二问】变限函数积分 ① 调换积分次序 ②分部积分

12、定积分物理应用


13、微分方程

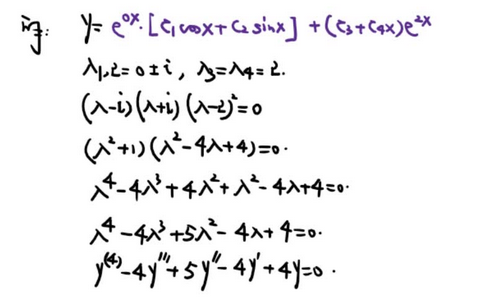
14、微分方程综合题
-- 给微分方程,求函数积分
当delta<0时,若是要求 解 有界,则 α小于等于 0,若要求 解 趋向于 0 ,则α <0


15、微分方程变换
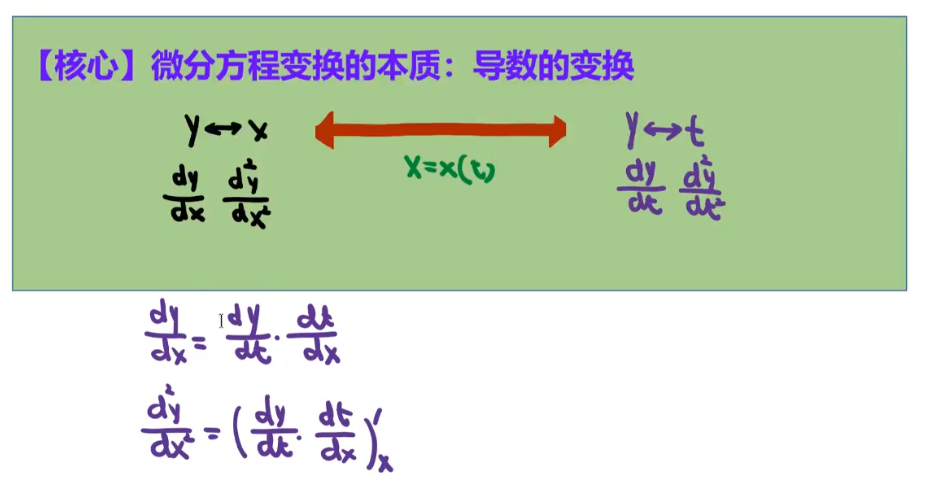

【回顾】2005年数二 真题 —— 与本题手法不同
~ 16、二元函数连续、可导、可微

17、多元复合函数偏导数计算

【已知复合 注意中间变量】

---- 多元函数变量代换
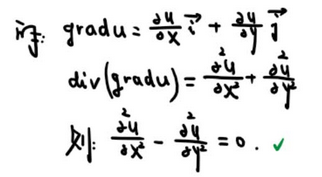
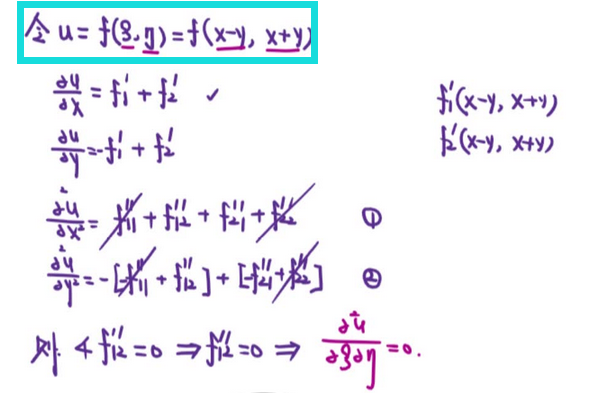


18、二元隐函数偏导数计算
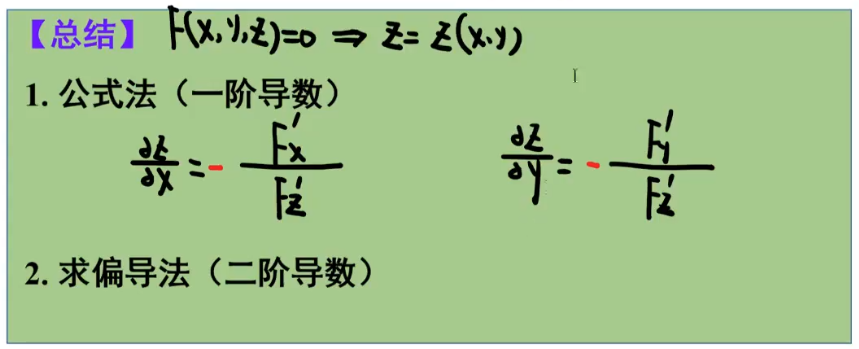
☆ 19、全微分(偏导数)反问题
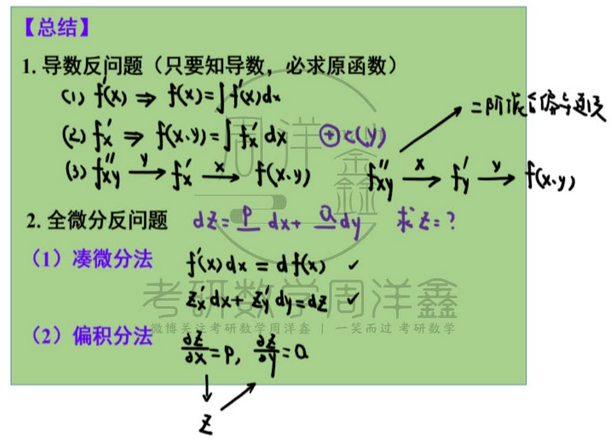
☆ 全微分方程
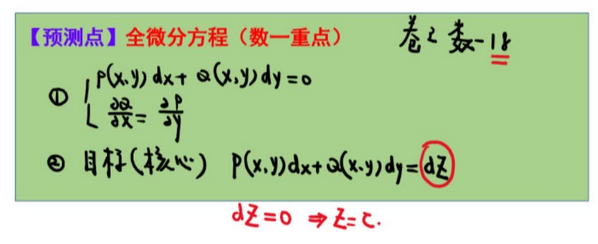

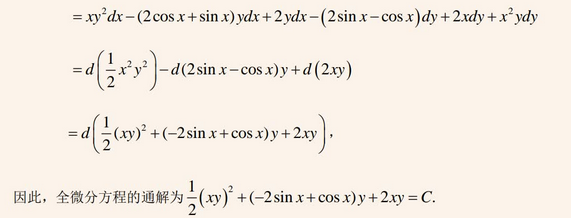

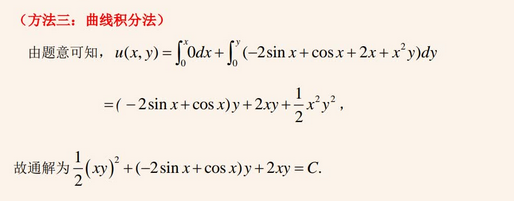
【再看一下思路】

20、多元函数极值、最值

- 多元函数同样可以用无穷小
【怎么解】

【再看一下思路】
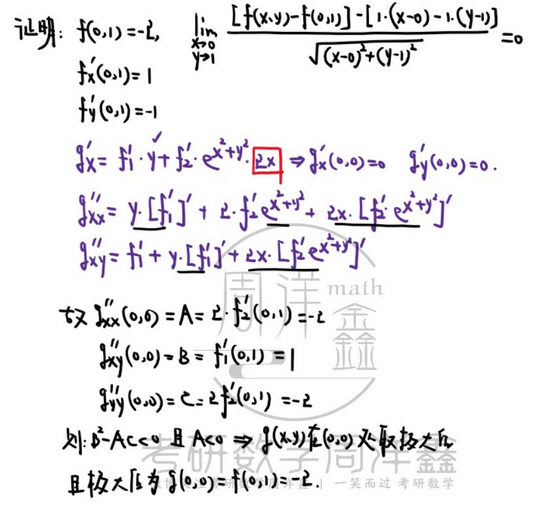
21、二重积分计算
【曲顶柱体的体积】
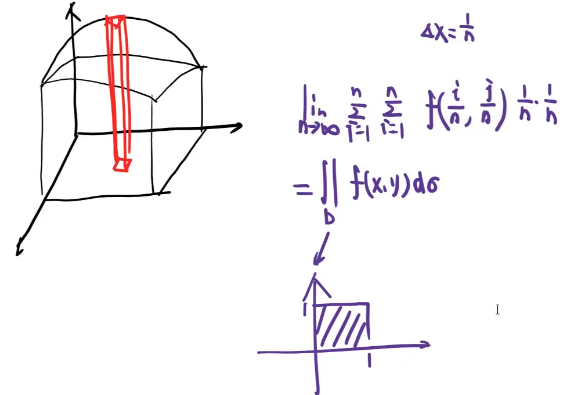

【可别忘了 轮换!】
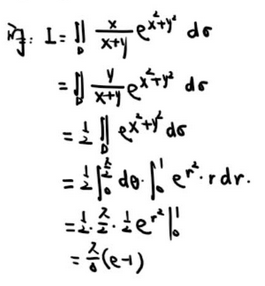

【积分不能代入x!不是一个x!】
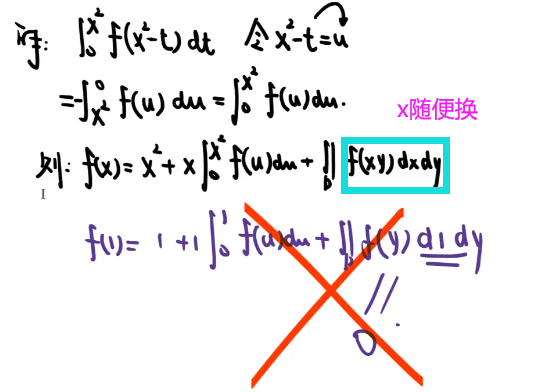

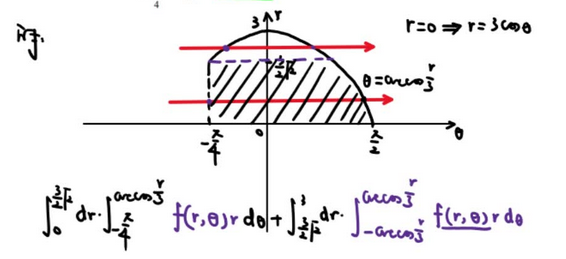
~ 22、二重积分换序

【这怎么画图 自己看】
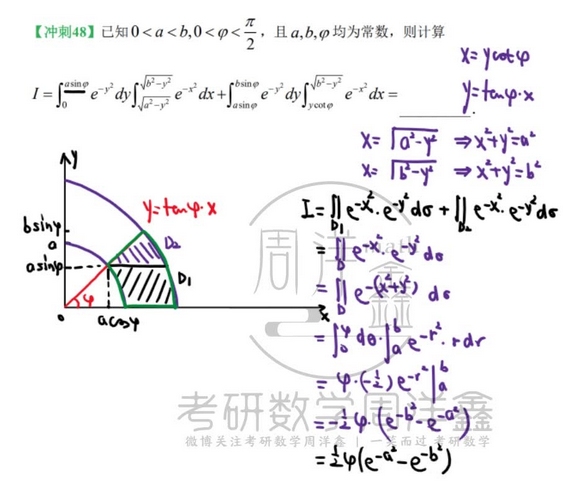
【极坐标极坐标互换!看成直角直接换】
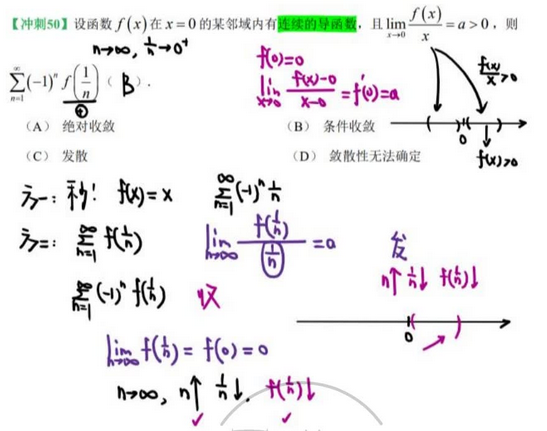
难 23、常数项级数审敛

相邻作差级数 只需通项极限存在
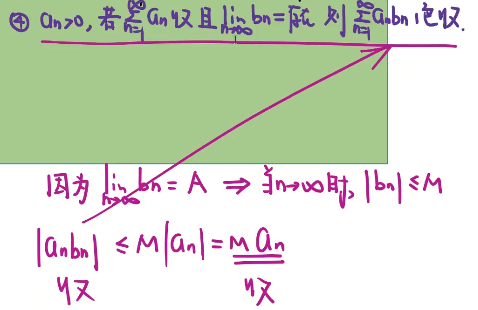

1、判断正项级数 —— 保号性 2、比值审敛法 3、极限为0,看单调性



24、幂级数求和

区间再现


25、幂级数展开


最后冲刺回顾:
-- 原函数写成变上限积分 + C


---- 泰勒公式的θ


--------------------------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------------------------
---- 拉格朗日ξ 的 另一种形式


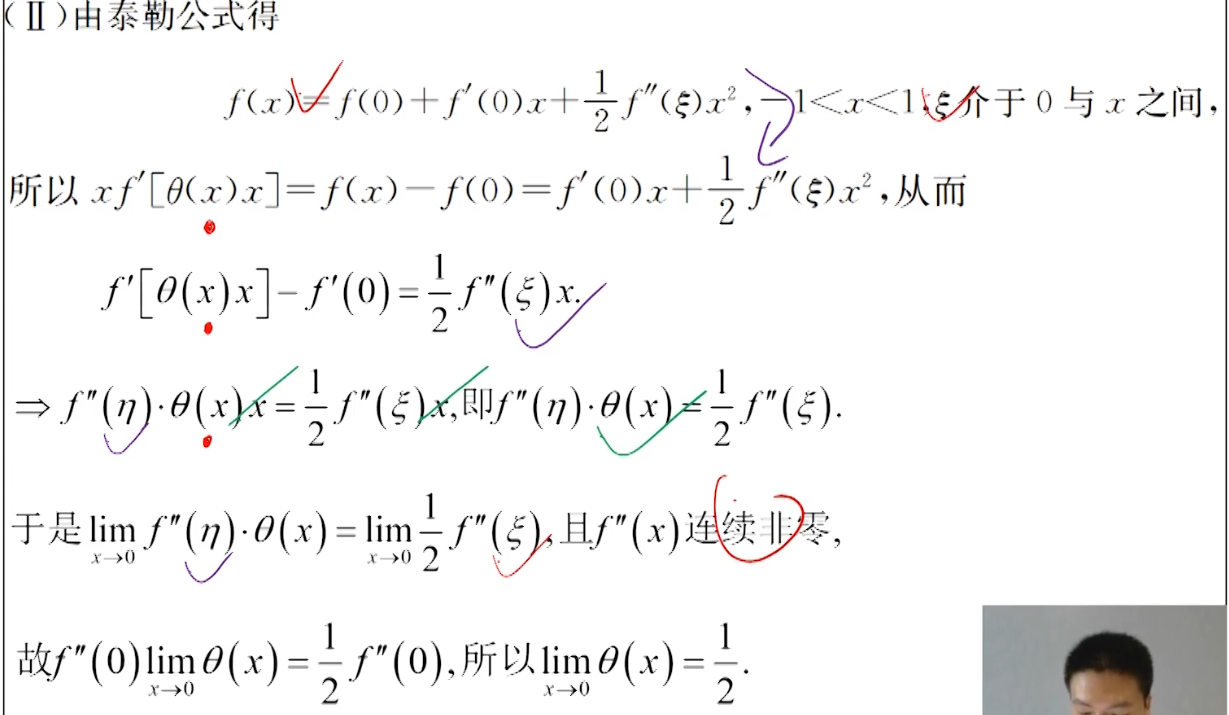
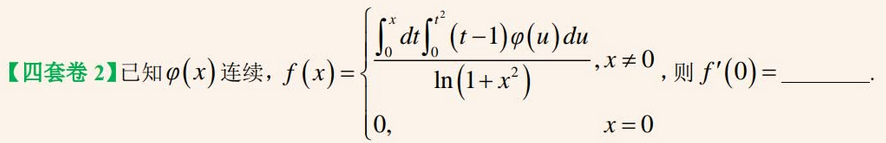

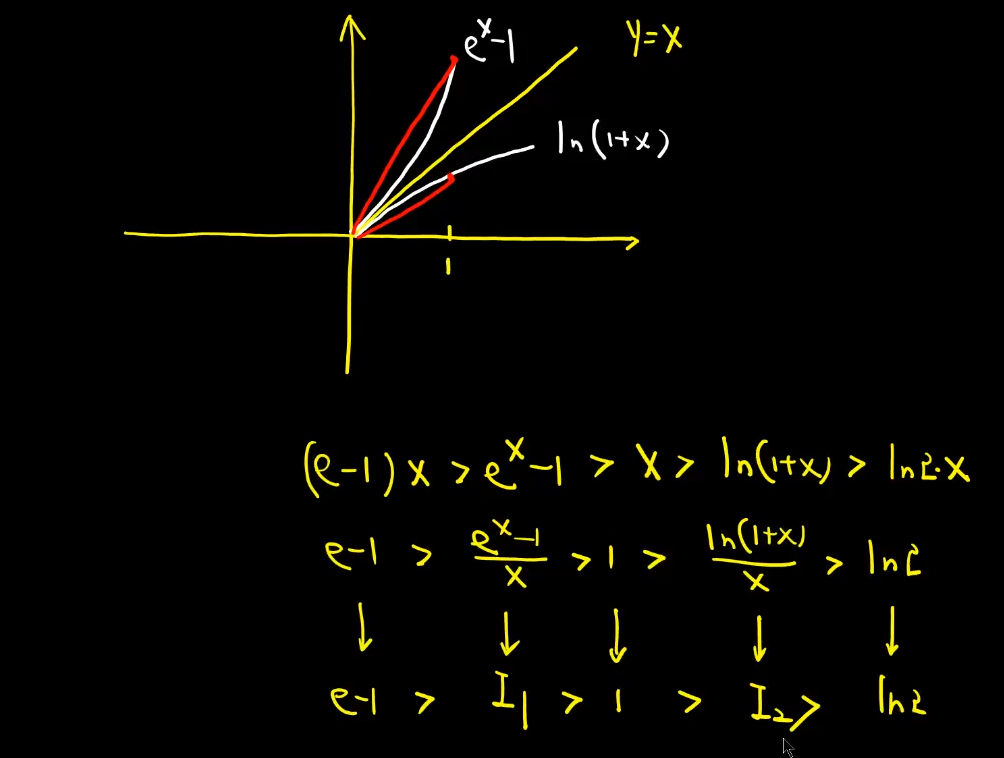
-- 特殊不等式
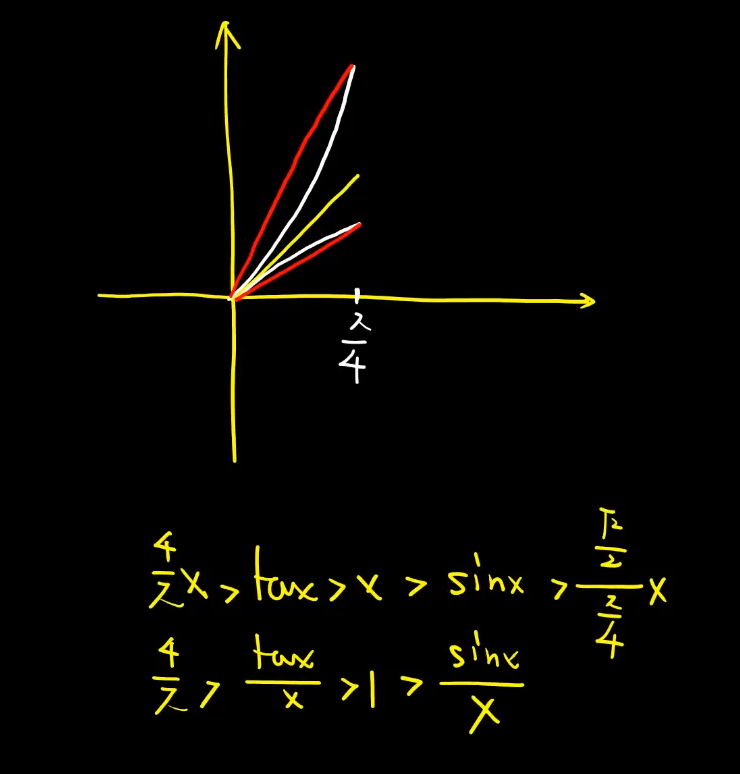
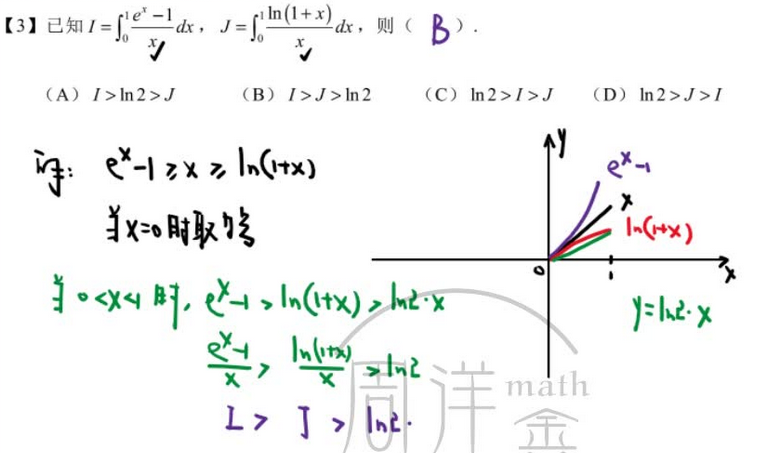
-- 求偏导,代入法
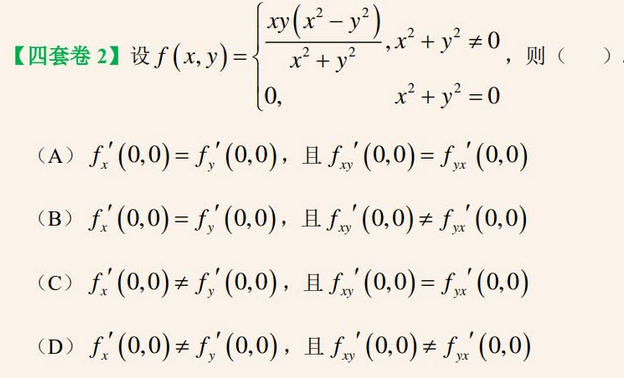

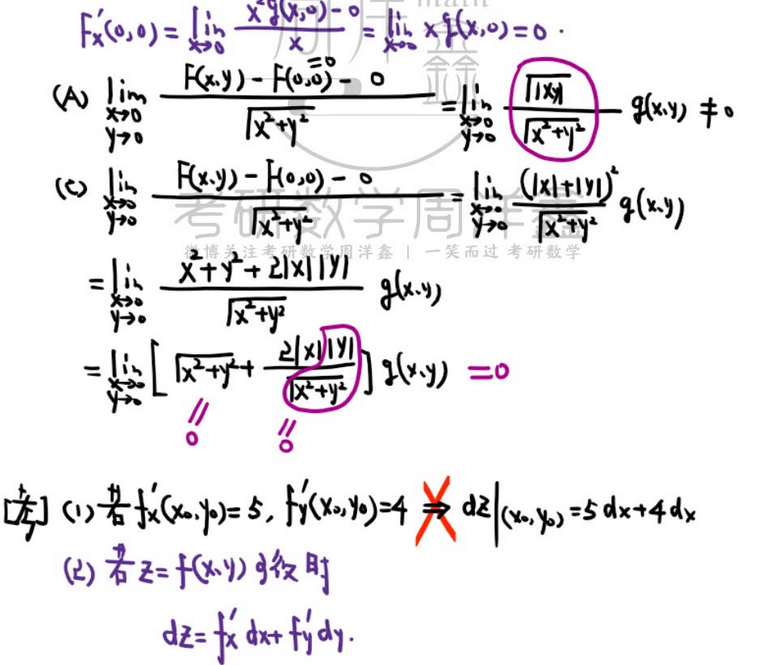
-- 偏导 d


--- 最后的级数
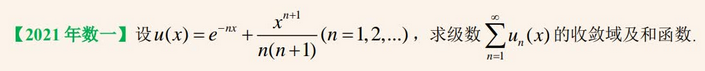




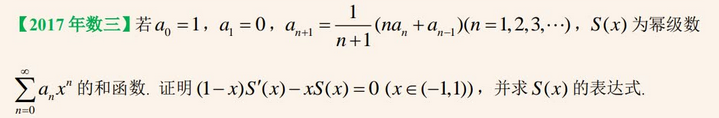


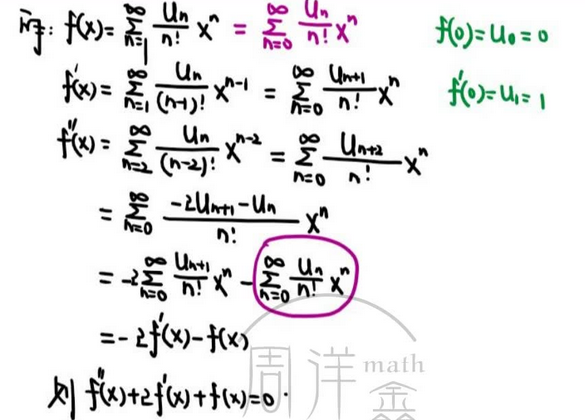

--- 最后的线面积分