263.丑数1

https://leetcode.cn/problems/ugly-number/description/

简单题，丑数只包含质因子2、3、5。所以直接使用 n 循环 除 2 3 5最后判断结果是否等于1即可。
代码：

class Solution {public boolean isUgly(int n) {if (n <= 0) return false;while (n % 2 == 0) n /= 2;while (n % 3 == 0) n /= 3;while (n % 5 == 0) n /= 5;return n == 1;}
}

264.丑数2

https://leetcode.cn/problems/ugly-number-ii/description/

上一题的进阶版本：需要我们找出第n个丑数，我们首先需要明确的是，对于一个具体的丑数 m 来说，他可能对应的下面三个丑数分别为 2 * m，3 * m，5 * m。

• 基于这个假设，我们创建一个数组 arr[n + 1] 其中arr[i] 表示的是第 i 个丑数。
• 同时为了计算出下一个丑数，我们需要保存三个指针，twoIdx，threeIdx，fiveIdx分别代表的含义为，丑数序列中与2 3 5 分别想乘的丑数对应的arr 数组的下标。
• 初始时，arr[1] = 1，表示第1个丑数为1。 twoIdx = 1，threeIdx = 1， fiveIdx = 1。此时为了计算第2 个丑数。我们可以如下计算：
  arr[2] = Math.min(arr[twoIdx] * 2, Math.min(arr[threeIdx] * 3, arr[fiveIdx] * 5))，计算出下一个最小的素数。同时计算完毕后，我们需要拿arr[2] 分别和 arr[twoIdx] * 2 、arr[threeIdx] * 3 、arr[fiveIdx] * 5对比，如果相等就更新下标，将对应下标 + 1，表示下一次质因子对应下一个质数。

具体参考代码示例：

class Solution {public int nthUglyNumber(int n) {int[] arr = new int[n + 1];arr[1] = 1;int twoIdx = 1, threeIdx = 1, fiveIdx = 1;for(int i = 2; i <= n; i++){int num = Math.min(arr[twoIdx] * 2, Math.min(arr[threeIdx] * 3, arr[fiveIdx] * 5));if(num == arr[twoIdx] * 2) ++twoIdx;if(num == arr[threeIdx] * 3)    ++threeIdx;if(num == arr[fiveIdx] * 5) ++fiveIdx;arr[i] = num;}return arr[n];}
}

1201.丑数3

https://leetcode.cn/problems/ugly-number-iii/

这个题目相当于是又一次升级版本，仍然是找出第n个丑数，但相对于上一题数据范围更大，我第一次仍然采用上一题思路，求解，最终通过了 43/53个测试用例。

参考题解解决：求解第n个质数，第n个质数一定包含n个质因子（与上面2道题目不同的地方是本题 1 不是质数）。所以我们需要做的就是求解一个数n，同时计算出他的质因子个数是否为n，如果是：说明我们找到了，如果不是需要采用二分的思路缩小搜索范围。
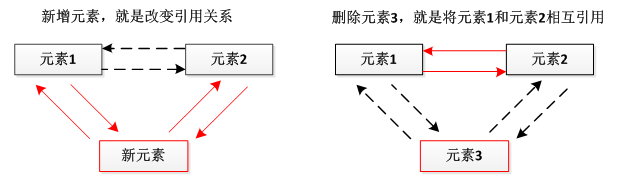
这个涉及到一个重复求解质因子的问题：互容原理：
参考：https://leetcode.cn/problems/ugly-number-iii/solutions/2003797/javac-rong-chi-yuan-li-er-fen-cha-zhao-b-bf69/
假设班里有10个学生喜欢数学， 15个学生喜欢语文， 21个学生喜欢编程，班里至少喜欢一门学科的有多少个学生呢？是10 + 15 + 21个吗？不是的，因为有些学生可能同时喜欢数学和语文，或者语文和编程，甚至还有可能三者都喜欢.

我们定义喜欢数学的学生为A集合，喜欢数学的学生为B集合，喜欢编程的为C集合。那么学生总数为∣A∪B∪C∣,如果直接将三个集合的个数相加即∣A∣+∣B∣+∣C∣会有重复个数，因此需要扣掉一些元素即∣A∩B∣,∣A∩C∣,∣B∩C∣,但是这时候我们发现∣A∩B∩C∣这部分又会被多扣一次，所以最后再加上这一部分。
∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣A∩C∣−∣B∩C∣+∣A∩B∩C∣

那么[1,i]中能够被a或b或c整除的数个数是否=i/a+i/b+i/c？,显然不等于，因为其中有些数即能被a，b和c整除。因此，我们要考虑如何去除重复计算的数。利用容斥原理，[1,i]中能被a或b或c整除的数的个数=i/a−i/b−i/c−i/ab−i/bc−i/ac+i/abc。其中i/ab代表能被a和b整除的数，其他同理。
如何利用以上信息计算答案呢?
题目需要返回第n个丑数，由于n很大，直接暴力求解显然不行。但是其实明白了上面的信息后，很容易就可以想到二分法来求解答案。
可以将题目转化为：在[1,i]中求解能被a或b或c整除的数个数之和大于等于n的最小的i即是我们的答案。
显然对于答案x来说，[1,x−1]必然是不满足要求，而[x,INF]都能够满足要求。那么就可以使用二分法来寻找这个问题的边界,左边界为1，右边界为无穷大。

代码参考：

class Solution {public int nthUglyNumber(int n, int a, int b, int c) {if(a == 1 || b == 1 || c == 1){return n;}long lcmab = lcm(a, b);long lcmac = lcm(a, c);long lcmbc = lcm(b, c);long lcmabc = lcm(lcmab, c);int min = Math.min(a, Math.min(b, c));long l = min, r = (long)Math.pow(min, n);while(l < r){long mid = l + (r - l) / 2;long count = mid / a + mid / b + mid / c - mid /lcmab - mid / lcmac - mid / lcmbc + mid / lcmabc;System.out.println("count:" + count + "mid :" + mid);if(n <= count){// 比如示例2:[6,8]区间有个数7此时7并不是质数r = mid;}else if(n > count){l = mid + 1;}}    return (int)(r);}// 最小公倍数public long lcm(long a, long b){return a * b / gcd(a, b);}// 最大公因数public long gcd(long a, long b){if(a == 0){return b;   }return gcd(b % a, a);}
}