作者：毛克彪1，2，3* ，张晨阳4，施建成5，王旭明2，郭中华2，李春树2，董立新6， 吴门新7，孙瑞静6，武胜利6，姬大彬3，蒋玲梅8，赵天杰3，邱玉宝3， 杜永明3，徐同仁8 （1. 中国农业科学院农业资源与农业区划研究所 北方干旱半干旱耕地高效利用全国重点实验室，北京 100081；2. 宁 夏大学 物理与电子电气工程学院，宁夏银川 750021；3. 中国科学院空天信息创新研究院 遥感科学国家重点实验 室，北京 100094；4. 北京大学 环境科学与工程学院，北京 100871；5. 中国科学院国家空间科学中心，北京 100190； 6. 国家卫星气象中心，北京 100081；7. 国家气象中心，北京 100081；8. 北京师范大学 地理科学部，北京 100875）

摘 要：人工智能 （Artificial Intelligence） 技术已在学术领域和工程应用掀起了研究高潮，在地球物理参数和农业 气象遥感参数反演方面也表现出了强大的应用潜力。目前大部分人工智能技术在地学和农学的应用还是“黑箱”， 应用没有物理意义或缺乏可解释性及通用性。本研究提出基于人工智能耦合物理和统计方法的地球物理参数反演 范式理论，即先基于物理能量平衡方程进行物理逻辑推理，从理论上构造反演方程组，然后基于物理推导构建泛 化的统计方法。通过物理模型模拟获得物理方法的代表性解以及利用多源数据获得统计方法代表性的解作为深度 学习的训练和测试数据库，最后利用深度学习进行优化求解。判定形成具有通用性和物理可解释的范式条件包括： （1） 输入与输出变量 （参数） 之间必须存在因果关系；（2） 输入和输出变量 （参数） 之间理论上可以构建闭合的 方程组 （未知数个数少于或等于方程组个数），也就是说输出参数可以被输入参数唯一确定。如果输入参数 （变 量） 和输出参数 （变量） 之间存在很强的因果关系，则可以直接使用深度学习进行反演。如果输入参数和输出参 数之间存在弱相关性，则需要添加先验知识来提高输出参数的反演精度。此外，本研究以农业遥感中的关键参数 地表温度、发射率、近地表空气温度和大气水汽含量联合反演作为案例对理论进行了证明，分析结果表明本理论 是可行的，并且可以辅助优化设计卫星传感器波段组合。本理论和判定条件的提出在地球物理参数反演史上具有 里程碑意义。

关键词：人工智能；深度学习；反演范式；物理逻辑推导；可解释；ChatGPT

引用格式：毛克彪, 张晨阳, 施建成, 王旭明, 郭中华, 李春树, 董立新, 吴门新, 孙瑞静, 武胜利, 姬大彬, 蒋玲梅, 赵天 杰, 邱玉宝, 杜永明, 徐同仁. 基于人工智能的地球物理参数反演范式理论及判定条件[J]. 智慧农业(中英文), 2023, 5 (2): 1-11. DOI：10.12133/j.smartag.SA202304013 MAO Kebiao, ZHANG Chenyang, SHI Jiancheng, WANG Xuming, GUO Zhonghua, LI Chunshu, DONG Lixin, WU Menxin, SUN Ruijing, WU Shengli, JI Dabin, JIANG Lingmei, ZHAO Tianjie, QIU Yubao, DU Yongming, XU Tongren. The Paradigm Theory and Judgment Conditions of Geophysical Parameter Retrieval Based on Artificial Intelligence[J]. Smart Agriculture, 2023, 5(2): 1-11. DOI：10.12133/j.smartag.SA202304013 (in Chinese with English abstract)

1 引 言

        ChatGPT的出现和升级使得人工智能进一步受到人们的广泛关注，人工智能成为新一轮产业变革的核心驱动力，将进一步释放科技创新的巨大能量，并创造新的强大引擎。人工智能与具体的行业结合将催生新技术和新产品，深刻改变人类思维和生产模式，实现社会和行业生产力的整体跃迁。深度学习是目前人工智能领域最重要的技术之一，在学术领域和工程应用掀起了研究高潮，并在自然语言生成模型、计算机视觉、语音识别等多个领域取得了显著的研究成果。鉴于深度学习在地学和农学领域的应用潜力和重要性，为促进人工智能在地学和农业领域的应用，必须加快人工智能与遥感技术的深度融合，为气象预报、农情监测和农业灾害预报等提供关键技术支撑［1-5］，为全球灾害监测和国家粮食安全服务。

        根据2022年《国家统计年鉴》，中国年均农业气象灾害受灾面积达1207.16万公顷，仅2022年气象灾害造成的直接经济损失就高达2386亿人民币。因此，快速准确获取农业气象关键参数信息对于科学指导农业气象防灾减灾、作物估产确保国家粮食安全等具有重要意义［6-8］。美国、日本和欧盟等相继研发气象卫星关键参数反演系统，中国自20世纪90年代开始研究气象卫星参数反演技术，虽然都已经取得了很大的进展，但仍然遇到一些瓶颈，如未知数多于方程的个数、相对入射角变化和混合像元等问题［9］。近年来，在计算机硬件技术和人工智能技术迅速发展相互辅助下，人工智能显示出了强大的优势［10］。因此研究如何将人工智能技术与地学，特别是与农业气象遥感参数传统反演物理和统计方法结合，发展具有物理意义和可解释的人工智能算法对提升遥感参数反演精度和对完善地球物理参数反演范式理论具有重要意义，同时为智慧农业和智慧地球提供关键的监测参数［11-14］。

2 地球物理参数反演范式理论与判定条件

        建立学科体系知识一般遵循三个步骤：首先从物理角度观察现象，其次用数学方法描述物理现象，最后从工程的角度去解决数学问题。“人工智能地球物理参数反演范式理论”可以表述为：如果目标信息（问题）在理论或物理逻辑上可以用数学方程描述（即可以在空间中可以形成唯一的解曲线），那么人工智能方法可以通过大数据学习和优化计算耦合物理方法和统计方法求解方程解。这使得耦合方法不但具有物理方法和统计方法各自的优势，同时充分利用了深度学习的优化计算能力，最大限度地提高了地球物理参数的反演精度。这样保证了反演范式不仅具有通用性，而且具有物理意义和可解释性。具体地，本研究提出的地球物理参数反演范式理论是使深度学习的输入参数（变量）和输出参数（变量）之间可以构建一套完整的闭合方程组。如果输入参数（变量）和输出参数（变量）之间存在强因果关系，则可以直接使用深度学习进行反演并获得高精度的反演结果。如果输入参数和输出参数之间存在弱相关性，则需要添加强相关性的先验知识和交叉迭代来提高输出参数的反演精度。可以通过物理模型模拟得到物理方法的大量代表性解，然后使用深度学习通过训练获得解的曲线函数。因此通过大数据模式的深度学习可以重复该物理方法。同时很多物理方法不能描述所有情况，为了克服物理方法的不足，基于物理逻辑推理，进一步构建泛化的统计方法，并通过多源数据获得统计方法的解来弥补物理方法的不足。其实从信息流传递的角度来说，深度学习网络更能符合现实情况，物理方法和统计方法是其中的部分表现形式。这些方法本质上一致，均是人们用来认识世界的一种手段，在不同认知程度上解读和解决现实问题。

        判定基于深度学习的地球物理参数反演形成是否具有通用性和物理可解释范式的条件有两个：

（1）深度学习的输入与输出变量（参数）之间必须存在因果关系，即在其他条件不变的情况下，改变任何一个输入变量，输出变量会发生变化。设深度学习输入变量为xi，输出变量为yj，则因果关系表示为公式（1）。

（2）深度学习的输入和输出变量（参数）之间理论上可以构建闭合的方程组（未知数个数少于或等于方程组个数），也就是说输出参数可以被输入参数唯一确定，用数学方程可以表示为公式（2）。

         为了使输出参数可以被输入参数唯一确定，需要满足k≥m这个条件。为论证深度学习的使用具有物理意义，在研究时必须进行物理逻辑推理。输入变量和输出变量之间存在因果关系且理论上也能构造足够的方程组时，如果输入变量和输出变量之间存在强相关性，则可以进行直接反演计算且可以保持高精度；但如果输入变量和输出变量之间是弱关系，要保证获得较高精度则需要利用强相关性变量作为先验知识。深度学习的应用不能脱离具体的问题或对象，如图1所示，本研究在解决某个应用问题时，首先要对问题对象进行物理逻辑推理，从理论上构造方程，确定输入变量和输出变量之间的因果关系；其次从方程里面的未知数个数确定方程组的个数，也就是确定几个输入参数能唯一确定输出变量；再次通过分析确定利用物理模型是否可以模拟得到所有代表性的解，如果得不到，则构建基于物理逻辑推理的泛化的统计方法［10,12］，利用多源数据补充代表性的解；然后利用大数据技术和深度学习优化求解物理和统计方法解的空间曲线函数；最后进行验证和反复迭代，达到精度后停止优化计算［12,13,15］。如果应用深度学习时，没有证明或不能证明存在上述两个条件，则一般认定深度学习的应用为“黑箱”［16,17］。如果能证明输入和输出参数之间肯定不存在闭合的关系（未知数个数大于方程组个数），那么这样的应用只适合于局部区域，不能通用和很难具备移植性，因此不能称为范式。

3 地球物理参数反演范式理论案例分析论证

3.1 物理逻辑推理　

        农业气象遥感关键参数是地球物理参数的重要组成部分，本研究以农业气象遥感关键参数为例对地球物理参数反演范式理论进行论证。

        首先进行物理逻辑推理。地表热辐射在通过大气达到卫星传感器的过程中，主要受地表类型和土壤水分（SoilMositure，SM）、地表温度（LandSurfaceTemperature，LST）、近地表空气温度（NearSurfaceAirTemperature，NSAT）和大气水汽含量（WaterVaporContent，WVC）等的影响。地表温度和土壤水分反演是基于地表热辐射传导及其通过大气到达传感器的传送物理过程，其反演方程通常可以用公式（3）描述，如图2所示。

        公式（3）中，Bλ（Tλ）（已知数）为卫星接收的星上辐射，(1-τλ(θ))(1+(1-ελ)τλ(θ))Bλ(Ta)为大气辐射贡献，Bλ(Ts)τλ(θ)ελ为地表辐射。其中，τλ(θ)为大气透过率（未知数），Ts为地表温度（未知数），Ta为近地表空气温度（未知数），ελ为地表发射率（未知数），即一个方程至少有4个未知数。需要说明的是观测角度其实也是一个未知数，每个像元中不同地物的组合导致相对入射角变化很大，很难准确地确定。由于地球物理参数之间存在内在的制约关系，可以利用卫星参数之间的相互制约关系减少一个未知数［18-21］。从图2可以看出，不同的参数之间是相互影响和纠缠的。氮磷钾溶解在土壤水分里面，土壤水分的变化影响介电常数变化，从而改变发射率，发射率变化影响地表的辐射效率，而地表温度变化决定土壤水分的蒸发速度，从而影响与近地表空气的能量交换和改变近地表空气温度以及大气剖面温度。理论上讲，土壤水分的变化也会影响热红外波段发射率的变化，但传统算法中没有考虑到这一点，一般认为热红外波段的发射率是相对不变的，其实也随土壤和植被含水量的变化而变化。因此在降雨比较多的地方，热红外遥感传统方法反演地表温度的精度波动相对较大，但人工智能方法可以克服这个困难。近地表空气温度的变化影响大气剖面，从而影响大气平均作用温度。在地表热辐射经过大气时，被大气水汽吸收，然后达到卫星传感器。因此，从物理逻辑推理可知［9,10,12,14］，单个方程中有4个未知数。如果没有先验知识，必须至少有4个热红外窗口波段从理论上构建反演方程；如果有大气水汽作为先验知识，也可以只需要3个热红外波段。以往大部分研究主要是针对单个参数进行反演，由于不同参数之间相互纠缠，利用人工智能方法进行联合反演和交叉迭代可以提高反演精度［9,10］。在进行物理逻辑推理后确定物理方法的理论构建后，在实际应用研究中发现，只利用物理模型建立的方法精度不是十分可靠，因为物理模型对真实世界进行了简化，而且很多地学模型也只适合部分情况［1-5］。因此，为了尽可能地满足更多的情况，还要基于物理逻辑推理进一步建立泛化的统计方法，这样才能保证方法的完整性和精度的可靠性［7-13］。MODIS卫星传感器是目前热红外波段数量和质量最好的传感器之一，本研究将针对MODIS的热红外波段进行模拟和论证分析。选定MODIS波段27/28/29/31/32/33（6.5~13.5μm），其中MODIS波段27、28和29在是热红外波段的水汽吸收区，波段31和32在热红外波段的窗口区，33波段在热红外波段窗口区的边缘上。将利用JPL（http：//speclib.jpl.nasa.gov）测量的地物波普曲线在MO‐DIS波段27/28/29/31/32/33的发射率作为MOD‐TRAN4的输入参数，地表温度变化范围为273~325K和近地表空气温度变化范围为273~320K。大气水汽含量变化范围0.1~4.0g/cm2，模拟观测角为0~45°。当角度过大时，由于斜路径上的水汽过大导致透过率过低，因此对这部分模拟数据进行了去除。将模拟数据随机分成两部分：训练数据45,650组，测试数据16,550组。根据传感器上获得不同参数信息量的多少，将不同的参数反演划分成三组，分别对地球物理参数理论和判别条件进行论证分析。第一组反演地表温度和发射率，主要分析和论证输入变量和输出变量之间的方程组个数和因果关系对反演精度影响；第二组反演近地表空气温度，主要分析和论证利用输入和输出变量之间强相关性变量作为先验知识，提高弱关系反演变量的精度；第三组反演大气水汽含量，主要分析论证当输入和输出变量之间存在强相关性时，添加先验知识可以提高反演稳定性，但对精度提高不明显。

 3.2 地表温度和发射率反演

        在3.1节的物理逻辑推理中可知，反演地表温度至少需要4个热红外波段组成辐射传输方程组，意味着当输入热红外波段少于4个时，反演精度不高。表1是波段29、31和32组合在给定条件下的理论反演精度。从表1中可以看出，当隐含层是9层且每层隐含节点都为700时，平均理论精度最高为1.13K，标准差为1.17K，相关系数为0.988。

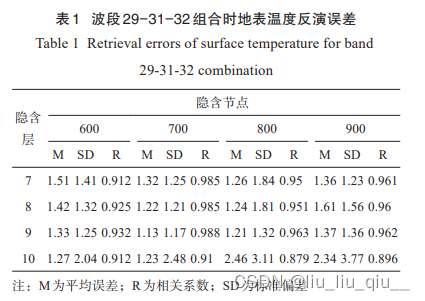
        表2是波段28-29-31-32组合反演的误差信息表。从表2中可以看出，当隐含层是9并且每层节点为800时反演精度最高。最高平均精度为0.45K，标准差为0.53K和相关系数为0.998。从表1和表2可以看出，当用4个热红外波段时，平均精度提高了0.68K。MODIS波段28是水汽吸收波段，增加热红外水汽吸收波段可以提高反演精度。当只用两个热红外波段（波段31和32）反演时，反演误差接近2K，因此传统劈窗算法必须获得大气水汽和地表发射率作为先验知识。而反演精度要达到1K以内，至少需要4个热红外波段，或者2个热红外波段加高精度的地表发射率和水汽作为先验知识，也就证明了基于人工智能的热红外遥感地表温度高精度反演需要理论上满足方程闭合的条件。

         表3是MODIS波段27-28-29-31-32波段组合时反演的地表温度误差信息表，从表3中可以看出当隐含层数9、每层隐含节点是900时，反演精度最高。平均最高精度是0.44K，标准差是0.52，相关系数是0.999。MODIS27波段也是水汽波段，增加水汽吸收波段能够提高水汽的精度，理论上可以提高整体反演精度。这里精度提高不明显，主要原因是波段27的地面辐射几乎很难穿透达到传感器，也就说透过率非常低，星上亮温主要包含的是高空大气水汽信息，因此对地表温度反演精度贡献不是非常大，但增加了反演的稳定性。

         表4是MODIS波段27-28-29-31-32-33作为输入参数时的反演误差信息表，当隐含层是8并且每层隐含节点为900时精度最高。平均精度最高为0.51K，标准差为0.55K，相关系数是0.997。从表3和4可以看出，当有汽波段时，添加波段33时并没有提高反演精度。主要原因是热红外波段33受CO2的影响比较大，不是非常适合于反演地表温度，因此增加热红外波段不一定会增加反演精度，有时反而会降低反演精度。表3分析说明当增加的波段与输出参数之间存在强相关性时，可以提高精度；表4说明当增加的波段与输出参数之间是弱关系或者是增加了噪声时，会降低反演精度。

         同时也可以将发射率反演计算出来，这里主要列出了波段27-28-29-31-32组合时波段31和32的发射率误差，如表5和表6所示，反演误差都在0.01以下。发射率在热红外波段相对被动微波受土壤水分变化的影响较小，能够用来表征地表类型。在微波波段，发射率受土壤水分的变化影响很大，地表温度和土壤水分通过发射率纠缠在一起［10］。

3.3 近地表空气温度反演　

        近地表空气温度是天气预报和农业干旱等模型的关键参数，以往主要是通过气象站点插值获取。也有一些研究通过统计方法或者神经网络从遥感数据中反演近地表空气温度，但通常缺乏可解释和物理意义，而且精度有限［9,15］。本研究采用深度学习和基于物理逻辑推理反演近地表空气温度，其推理和分析过程请参考文献［9］和［15］。在热红外遥感窗口波段，热红外传感器获取的主要信息来自地表，近地表空气温度的信息量相对较少，因此反演精度受限。表7是MODIS波段27-28-29-31-32组合时直接反演近地表空气温度的误差信息表，当隐含层是10和每层隐含节点是700时精度最高。理论平均精度最高为1.42K，标准差为1.46K，相关系数0.975。

        表8是波段27-28-29-31-32+LST+LSE31+LSE32组合时近地表空气温度的反演误差（其中，LSE31为波段31发射率，LSE32为波段32发射率），最高精度是在隐含层为10和每层隐含节点为800时，最高平均精度为0.81K，标准偏差为0.91K，相关系数为0.984。当利用地表温度和发射率作为先验知识时，近地表空气温度的精度明显得到提高，而且反演精度更加稳定。这主要是因为利用地表温度作为先验知识放大了近地表空气温度的信号，而且发射率提供了地表类型，因此反演精度大幅提高，并且算法更具移植性［9］。因此对于输入变量与输出变量之间是弱相关的参数反演，加入强相关性的变量作为先验知识可以提高弱相关参数的反演精度。

3.4 大气水汽含量反演　

        大气水汽含量是天气预报和农业干旱监测等模型的重要参数，在上面分析的基础上，表9是波段27-28-29-31-32组合时的大气水汽含量反演误差。最高精度是在隐含层数为9和每层隐含节点为800时，最高平均精度为0.09g/cm2，标准偏差为0.11g/cm2，相关系数为0.989。

        表10是波段27-28-29-31-32+LST+LSE组合时的大气水汽含量反演误差，最高精度是在隐含层为9和每层隐含节点为900时，最高平均精度为0.08g/cm2，标准偏差为0.09g/cm2，相关系数为0.992。对比表9和表10，当使用LST和LSE作为先验知识时，精度略有提高和误差相对比较稳定。如果当先验知识LST和LSE具有一定误差时，可能精度不会有太大的改善。因此，当输入参数中有2个输入波段对输出参数水汽比较敏感时，可以不加入先验知识。

4 讨 论

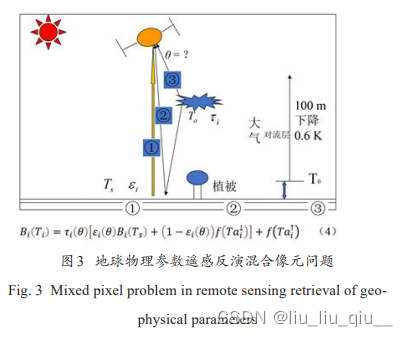
        人类认识世界通过观察（取样），然后基于观察和思考用大脑抽象构造模式，最大程度地形成知识以达到快速认识世界或者目标的目的，本质上可以归结为定义规则认识世界。目标只有一个——最大程度地提高识别（认知）精度，因此不必过于考虑具体方法的形式（统计方法或物理方法或人工智能方法），这些都是认知的手段。根据作者团队多年的研究经验，统计方法、物理方法和机器学习方法本质上是一致的，是人们根据不同的情况定义的认识事物规律的一种方法或手段，特别是目前用得比较多的深度学习神经网络算法其实是一种更高级的统计优化计算方法，这种方法的精度和普适范围取决于构建样本库（训练和测试数据的代表性和精度）时遵循的规则是否更符合真实情况。传统遥感地球物理参数反演方法主要适合于地势平坦，地表类型单一的纯净像元。如图3所示，对于地球物理遥感参数反演，传统的物理方法无法解决像元相对入射角问题，也很难解决混合像元问题，从而导致传统方法反演精度具有瓶颈，公式（4）中参数的物理意义具体请参考文献［9,15］。人工智能方法可以将混合像元当成一个新的等效地物类型，在解决复杂像元反演问题上具有比传统物理方法非常强的优势。从能量信息流传播的角度看，深度学习神经网络通过神经元控制传递能量的方式比统计和物理方法更接近真实情况，甚至更具有物理意义，这需要人们提高或改变认知思维，并从信息传播的角度解读［1,10］。因此只要深度学习耦合物理和统计方法的模式满足范式条件，理论上可以无限逼近真实情况。

        另外，从某个角度上讲，人工智能是一种高级的优化计算方法，与物理方法和统计方法在本质上是一样的，都是识别目标的手段。只不过机器学习方法在硬件技术高速发展的辅助下，显示出更加强大的识别目标的迭代优化计算能力，深度学习理论上可以将很多组不同物理方法和统计方法耦合在一起。在满足反演范式条件下，深度学习的反演和适应范围理论上远远胜过一个或者几个物理和统计传统方法的组合。作者团队在2006年和2007年将深度学习（动态学习神经网络）应用于地表温度和发射率反演［19-21］，但当时由于计算机内存不够，隐含层一般只设置了3层，而现在算法的隐含层和内存翻到了几倍甚至几十倍上百倍［1，12］，对计算机要求更高。由于计算机技术的进步，目前地球物理参数遥感反演的精度也大幅提升。在满足范式条件下，基于人工智能的深度学习耦合物理和统计方法范式是目前利用遥感数据反演地球物理参数特别是农业气象遥感关键参数的最佳方法。本文主要讨论的是地球物理参数反演范式理论和判定条件，其对于遥感分类或者目标识别也同样适用［22,23］。目前卷积神经网络（ConvolutionalNeu‐ralNetwork，CNN）被认为是较好的分类和目标识别方法之一，其实CNN是在传统神经网络的基础上进一步利用不同的卷积核从不同的尺度上提取目标的信息，目的就是通过不同维度的信息来唯一确定目标，从而达到提高分类（目标识别）的精度［24］。理论上讲，如果这些从不同维度（不同卷积核）上提取的信息也可以构建数学方程唯一确定输出参数，也可以形成范式，否则同样也存在不确定性。

 5 结 论

         最近几年，人工智能在许多领域的突破催生了很多新技术、新产品和新产业，将深刻影响和改变人类生产生活方式和思维模式，实现生产力的整体跃升。为了促进人工智能在地学和农学的应用和培养交叉学科的人才，本研究提出了基于人工智能地球物理参数反演范式理论及判定条件，即通过物理逻辑推理，目标信息（问题）在理论或物理逻辑上可以用数学表达式进行描述，同时可以用物理模型模拟获得物理方法的解。为了克服物理方法的缺陷，基于物理逻辑推理构建泛化的统计方法，并且通过多源数据获得统计方法的解。在此基础上，物理方法和统计方法的解构成深度学习的训练和测试数据，从而达到深度学习耦合物理和统计方法的目的。深度学习通过大数据学习和优化计算将物理方法和统计方法相结合，从而保证了提出的范式不仅有物理意义和可解释性，而且还具备通用性。

        人工智能方法反演地球物理参数是否形成范式，即形成具有物理机理和可解释的深度学习范式基本条件有两个：（1）输入与输出变量（参数）之间必须存在因果关系；（2）输入和输出变量（参数）之间理论上可以构建闭合的方程组（未知数个数少于或等于方程组个数），也就是说输出参数可以被输入变量唯一确定。如果使用深度学习没有证明或不能证明存在上述两个条件，我们一般认定为“黑箱”。如果能证明：输入和输出参数之间肯定不存在闭合的关系（未知数大于方程组个数），那么这样的应用可能主要适合于局部区域，不能通用，很难具备移植性，不能称为范式。

        人工智能方法的应用不能脱离具体的问题，我们在解决某个应用问题时，要先对问题对象进行物理逻辑推理，从理论上构造方程，确定是输入变量和输出变量之间的因果关系；然后从方程里面的未知数个数确定方程组的个数，也就是确定几个输入参数，最后使用深度学习进行优化求解。本文首先进行物理逻辑推理是使得深度学习具有物理意义和可解释的关键。利用MODIS遥感数据反演地表温度、发射率、近地表空气温度和大气水汽含量对范式理论进行了论证：当输出参数（LST和LSE）与输入变量（BT）i之间具有强相关性时，利用深度学习耦合物理和统计方法可以获得非常高的精度；当输出参数（NSAT）与输入变量（BT）i之间是弱相关性时，加入先验知识（LST和LSE）可以提高输出参数（NSAT）反演精度和稳定性；部分强相关性时（WVC与BT），i加入先验知识（LST和LSE）虽然能稍微提高精度和稳定性，但先验知识（LST和LSE）的误差可能带来不确定性，因此也可以不加入先验知识。通过对MODIS传感器热红外波段地球物理参数反演分析可知，波段27、28、29、31更适合于反演大气水汽含量，波段28、29、31和32更适合于反演地表温度和发射率及近地表空气温度。如果要获得4个参数的最高精度，则建议仪器设计5个波段（27、28、29、31、32）最合适。如果只设计4个热红波段，可以优先考虑27、28、31、32。本研究分析结果表明地球物理参数反演范式理论和判定条件可靠，该理论和判定条件的提出对利用人工智能方法反演地表物理参数具有重大意义。

        地球物理参数反演范式理论和判定条件也适用于遥感分类等目标识别，只是需要换一个角度解读，比如不同卷积核提取的特征信息要能唯一确定目标。在满足范式条件下，基于人工智能反演地球物理参数是最佳选择，因此建议科技部和国家自然基金委给予支持，打造中国基于人工智能的地球物理参数反演范式的“ChatGPT”。

 利益冲突声明：本研究不存在研究者以及与公开研究成果有关的利益冲突。

参考文献：[1 ] 毛克彪. 基于热红外和微波数据的地表温度和土壤水分 反演算法研究[M]. 北京: 中国农业科学技术出版社, 2007. MAO K B. The study of algorithm for retrieving land sur‐ face temperature and soil moisture from thermal and microwave data[M]. Beijing: China Agricultural Science and Technology Press, 2007.

[ 2 ] 毛克彪, 施建成, 覃志豪, 等. 一个针对ASTER数据同时 反演地表温度和比辐射率的四通道算法[J]. 遥感学报, 2006, 10(4): 593-599. MAO K B, SHI J C, QIN Z H, et al. A four-channel algo‐ rithm for retrieving land surface temperature and emissivi‐ ty from ASTER data[J]. Journal of remote sensing, 2006, 10(4): 593-599.

[ 3 ] 毛克彪, 王道龙, 李滋睿, 等 . 利用 AMSR-E被动微波数 据反演地表温度的神经网络算法[J]. 高技术通讯, 2009, 19(11): 1195-1200. MAO K B, WANG D L, LI Z R, et al. A neural network method for retrieving land-surface temperature from AM‐ SR-E data[J]. Chinese high technology letters, 2009, 19 (11): 1195-1200.

[ 4 ] MAO K B, SHEN X Y, ZUO Z Y, et al. An advanced radi‐ ative transfer and neural network scheme and evaluation for estimating water vapor content from MODIS data[J]. Atmosphere, 2017, 8(8): ID 139.

[ 5 ] MAO K B, MA Y, XIA L, et al. A neural network method for monitoring snowstorm: A case study in Southern China[J]. Chinese geographical science, 2014, 24(5): 599-606.

[ 6 ] HAN J Q, MAO K B, XU T R, et al. A soil moisture esti‐ mation framework based on the CART algorithm and its application in China[J]. Journal of hydrology, 2018, 563: 65-75.

[ 7 ] TAN J C, NOURELDEEN N, MAO K B, et al. Deep learning convolutional neural network for the retrieval of land surface temperature from AMSR2 data in China[J]. Sensors, 2019, 19(13): ID 2987.

[ 8 ] MAO K B, ZUO Z Y, SHEN X Y, et al. Retrieval of landsurface temperature from AMSR2 data using a deep dy‐ namic learning neural network[J]. Chinese geographical science, 2018, 28(1): 1-11.

[ 9 ] DU B Y, MAO K B, BATENI S M, et al. A novel fully coupled physical–statistical–deep learning method for retrieving near-surface air temperature from multisource data[J]. Remote sensing, 2022, 14(22): ID 5812.

[10] MAO K B, WANG H, SHI J C, et al. A general paradigm for retrieving soil moisture and surface temperature from passive microwave remote sensing data based on artificial intelligence[J]. Remote sensing, 2023, 15(7): ID 1793.

[11] MAO K B, LI S M, WANG D L, et al. Retrieval of land surface temperature and emissivity from ASTER1B data using a dynamic learning neural network[J]. International journal of remote sensing, 2011, 32(19): 5413-5423.

[12] MAO K B, SHI J C, LI Z L, et al. An RM-NN algorithm for retrieving land surface temperature and emissivity from EOS/MODIS data[J]. Journal of geophysical re‐ search: Atmospheres, 2007, 112(D21): ID D21102.

[13] WANG H, MAO K B, YUAN Z J, et al. A method for land surface temperature retrieval based on model-dataknowledge-driven and deep learning[J]. Remote sensing of environment, 2021, 265: ID 112665.

[14] 毛克彪, 杨军, 韩秀珍, 等 . 基于深度动态学习神经网络 和辐射传输模型地表温度反演算法研究[J]. 中国农业信 息, 2018, 30(5): 47-57. MAO K B, YANG J, HAN X Z, et al. Retrieving land sur‐ face temperature based on deep dynamic learning NN al‐ gorithm and radiation transmission model[J]. China agri‐ cultural informatics, 2018, 30(5): 47-57.

[15] MAO K B, TANG H J, WANG X F, et al. Near-surface air temperature estimation from ASTER data based on neural network algorithm[J]. International journal of remote sens‐ ing, 2008, 29(20): 6021-6028.

[16] MAO K B, MA Y, SHEN X Y, et al. Estimation of broad‐ band emissivity (8-12um) from ASTER data by using RMNN[J]. Optics express, 2012, 20(18): 20096-20101.

[17] MAO K B, LI H T, HU D Y, et al. Estimation of water va‐ por content in near-infrared bands around 1 μm from MO‐ DIS data by using RM-NN[J]. Optics express, 2010, 18 (9): 9542-9554.

[18] MAO K B, SHI J C, TANG H J, et al. A neural network technique for separating land surface emissivity and tem‐ perature from ASTER imagery[J]. IEEE transactions on geoscience and remote sensing, 2008, 46(1): 200-208.

[19] MAO K, SHI J, LI Z, et al. A multiple-band algorithm for separating land surface emissivity and temperature from ASTER imagery[C]//2006 IEEE International Symposium on Geoscience and Remote Sensing. Piscataway, NJ, USA: IEEE, 2007: 1358-1361.

[20] 毛克彪, 唐华俊, 李丽英, 等. 一个从MODIS数据同时反 演地表温度和发射率的神经网络算法[J]. 遥感信息, 2007, 22(4): 9-15, 8. MAO K B, TANG H J, LI L Y, et al. An NN algorithm for retrieving land surface temperature and emissivity from MODIS data[J]. Remote sensing information, 2007, 22 (4): 9-15, 8.

[21] 毛克彪, 唐华俊, 陈仲新, 等 . 一个用神经网络优化的针 对 ASTER 数据反演地表温度和发射率的多波段算法 [J]. 国土资源遥感, 2007, 19(3): 18-22. MAO K B, TANG H J, CHEN Z X, et al. An optimizaed multiple-band algorithm by using neural network for sepa‐ rating land surface emissivity and temperature from aster imagery[J]. Remote sensing for land & resources, 2007, 19 (3): 18-22.

[22] 毛克彪, 覃志豪, 张万昌. 针对ETM基于BP网络像元分 解模型分类研究[J]. 遥感信息, 2004, 19(2): 27-30. MAO K B, QIN Z H, ZHANG W C. The research of un‐ mixing landsat ETM data based on BP ANN[J]. Remote sensing information, 2004, 19(2): 27-30.

[23] 毛克彪, 覃志豪, 张万昌. 一个基于SOFM网络模型的遥 感 图 像 分 类 方 法 [J]. 遥 感 技 术 与 应 用 , 2003, 18(6): 399-403. MAO K B, QIN Z H, ZHANG W C. A method of classifi‐ cation of remote sensing based on SOFM model[J]. Re‐ mote sensing technology and application, 2003, 18(6): 399-403.

[24] 付秀丽, 黎玲萍, 毛克彪, 等 . 基于卷积神经网络模型的 遥感图像分类[J]. 高技术通讯, 2017, 27(3): 203-212. FU X L, LI L P, MAO K B, et al. Remote sensing image classification based on CNN model[J]. Chinese high tech‐ nology letters, 2017, 27(3): 203-212.