洛谷P5648

这题花了很长时间，是在线段树题单里找到的（）。有线段树做法，但是我感觉可能比倍增做法更难看懂。以后有空再看看吧。感觉线段树现在只会板子题，绿稍微难点可能就不会。

花了很久时间之后，就觉得自己有必要去发一篇博客来纪念一下，毕竟花了这么久的时间。中午看的时候，突然发现线段树我不知道怎么弄……然后只能看题解了，感觉看着都很麻烦的，我真的感觉自己很难看懂题解，有主席树和线段树做法，但是我有点不太懂，倍增也有点不懂。

然后晚上，让 chat 给我解释了一下，就看得差不多了。其实大佬写的题解很好，只是我有些变量其实没看懂干啥用的，没仔细看吧，但是幸好现在已经解决了。后来交的时候一直 RE , WA ，改了几个东西之后过了，现在也想明白原因了。

题目大意

给你一个数组 $a$ , 给出 $q$ 次询问，每次给出 $l, r$ ，求下列式子的和。
$\sum_{i=l}^{r} \max_{l\le j\le i}a_j$

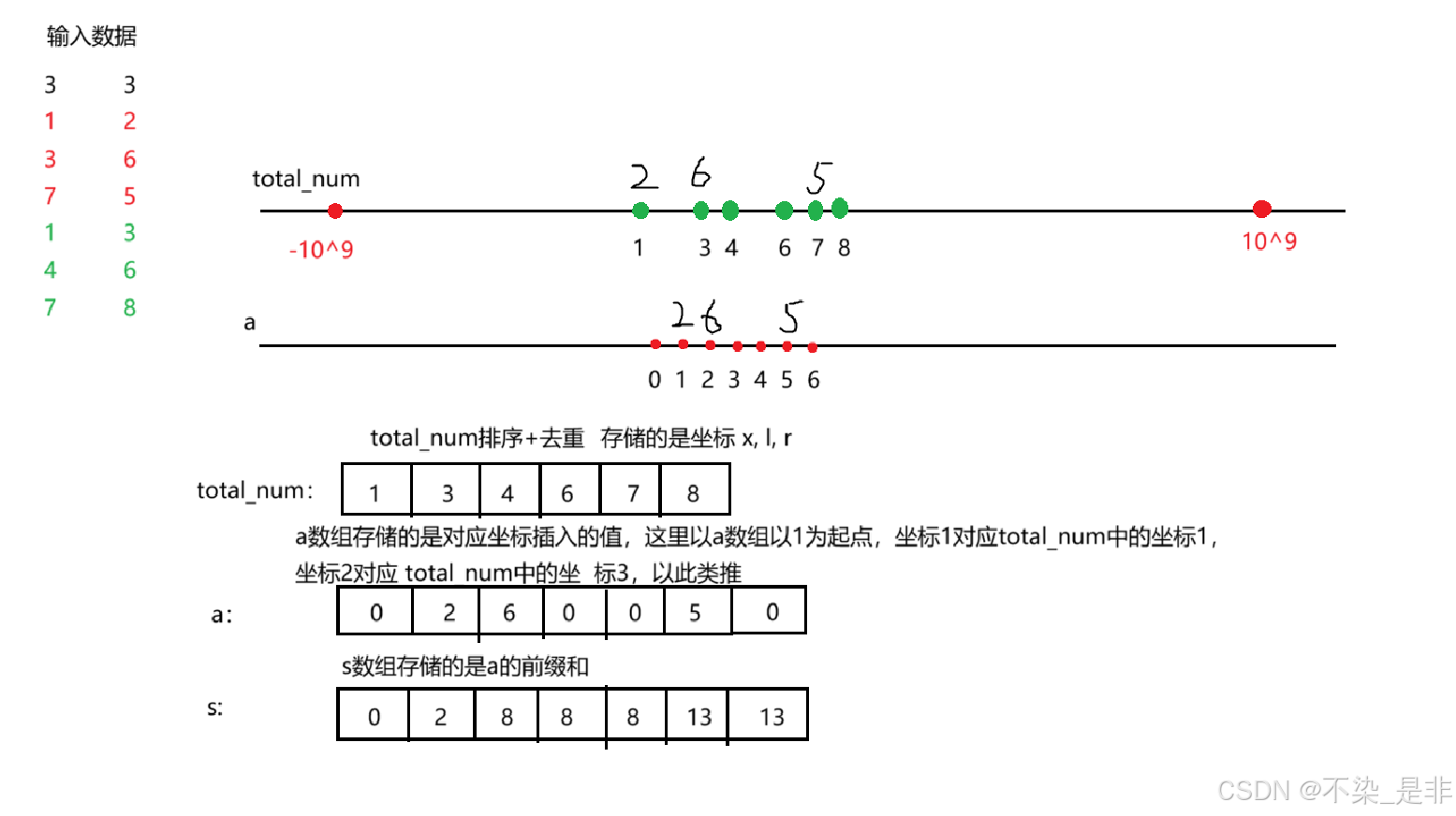
如果 $l$ 确定，那么 $a_l$ 一定会被一直加直到下一个最大值出现或者 $i > r$ ，所以相当于我们一个数字在它和它的下一个最大值出现之前，一直会被加。所以我们可以预处理出每一个 $a_i$ 的下一个比它大的数字，这样做只能拿 $90$ 分看讨论区说。如果遇到一直递增的数据，复杂度就很高。

可以使用倍增， $nxt_{i,j}$ 表示从第 $i$ 个点跳转到的下一个点，这里跳转指的其实就是它后面的第多少个新的最大值。用 $f_{i,j}$ 表示 $i$ 跳转 $2^j$ 个点的答案。

然后就有

$nxt_{i,j}=nxt_{nxt_{i,j-1},j-1}$

$f_{i,j}=f_{i,j-1}+f_{nxt_{i,j-1},j-1}$

第一个式子是显然的，但第二个式子我想了很久，虽然确实很简单，当时我没太理解 $n x t$ 数组吧，其实就是只会跳转到比它大的数字，所以后面那部分的答案就不用再考虑前面的部分。线段树做法貌似也是这样的思路，以后看看。

//created: 2024-10-08 20:27:01
// #define SKADI
#if defined(YUANSHEN)
#include<D:/Tovi/template/my_template.hpp>
#else
#include<bits/stdc++.h>
using namespace std;
#endif
#ifndef SKADI
#define dbg(...) 42
#endif
template <typename T1, typename T2> void cmin(T1 &x, const T2 &y) {
x = x < y ? x : y;
}
template <typename T1, typename T2> void cmax(T1 &x, const T2 &y) {
x = x > y ? x : y;
}
using ll = long long;
using ull = unsigned long long;
using pii = pair<int,int>;
using pll = pair<ll,ll>;
#define fixset(x) fixed<<setprecision(x)
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(),(x).end()
#define ALL(x) (x).begin()+1,(x).end()
const int INF = 1000000000;
const ll LNF = 1000000000000000000;const int N = 5e5+10;
ll f[N][22];
int n,a[N],nxt[N][22];void init()
{vector<int>stk;//nxt[i][0]找到的是右边第一个比a[i]大的数字的下标，用单调栈就行for(int i=1;i<=n;i++){while(!stk.empty()&&a[stk.back()]<a[i]){nxt[stk.back()][0]=i;stk.pop_back();}stk.push_back(i);}while(!stk.empty()){nxt[stk.back()][0]=n+1;stk.pop_back();}//剩下的说明没有数字比它大 所以就弄成n+1，而且能确保所有点都被初始化nxt[n+1][0]=n+1;//这个一定要，后面会用到的for(int i=1;i<=n;i++){f[i][0]=1LL*a[i]*(nxt[i][0]-i);}//很显然，这一部分的和就等于a[i]直接乘以a[i]是最大值的区间长度for(int i=1;i<=21;i++){for(int j=1;j<=n+1;j++)//边界一定要n+1nxt[j][i]=n+1;for(int j=1;j+(1<<i)<=n+1;j++){//因为这里更新的话，如果你前面这个nxt已经是最大的话，那么这里nxt[n+1][]会没有，如果不初始化nxt[j][i]=nxt[nxt[j][i-1]][i-1];f[j][i]=f[j][i-1]+f[nxt[j][i-1]][i-1];}}
}
void solve()
{int q;cin>>n>>q;for(int i=1;i<=n;i++)cin>>a[i];init();ll lst=0;//这里也开 ll ，有可能超的，而且小心异或边负数了while(q--){ll l,r;//注意开ll ， 看讨论区有人说可能爆int cin>>l>>r;l=1+(l^lst)%n;r=(r^(lst+1))%(n-l+1)+l;ll cur=0,pos=l;for(int i=21;i>=0;i--){if(nxt[pos][i]>r) continue;cur+=f[pos][i];pos=nxt[pos][i];}cur+=1LL*a[pos]*(r-pos+1);//注意别爆了lst=cur;cout<<lst<<'\n';}
}int main()
{
#ifndef SKADIios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#endifint T=1;// cin>>T;while(T--)solve();return 0;
}

感觉这题对我真挺有难度的，感谢各位大佬的题解。我本来半天没找到自己哪写错了，刚开始一直 $RE$ ，然后 $W A$ ，都是样例能过但分数 $0$ ，等等，为啥 $RE$ 来着，好像又想不明白了来着。

$O K$ ，找到了， $RE$ 是因为没开 $ll$ 然后异或成负数了然后下标为负了就寄了吧，这数据挺好的哈，全部 $RE$ 。洛谷的讨论区真是个好东西，感谢各位大佬。然后 $W A$ 是因为初始话没有初始化 $nxt_{n+1,i}$ 导致很多 $n x t$ 变成 $0$ 了。这个很久很久才看出来，还是我突然才想起来得对拍一下才发现的。