513. 找树左下角的值
题目
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
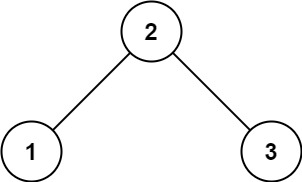
输入: root = [2,1,3] 输出: 1
题目解析---迭代法
层序遍历,然后只需要记录最后一行第一个节点的数值就可以了。
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*>que;if(root!=NULL)que.push(root);int result=0;while(!que.empty()){int size=que.size();for(int i=0;i<size;i++){TreeNode*node=que.front();que.pop();if(i==0)result=node->val;if(node->left)que.push(node->left);if(node->right)que.push(node->right);}}return result;}
};112. 路径总和
题目
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
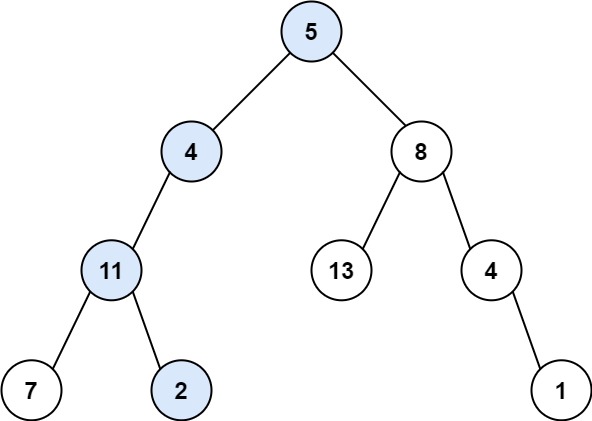
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
题目解析---递归法
这里使用深度优先遍历数组
递归三步走
确定参数和返回值
参数:需要二叉树的根节点,以及记录路径的数组path,以及传递target
确定终止条件
访问到叶子节点就终止,并且在此时进行比较,如果记录的路径和等于target,则返回true
确定单层递归的逻辑
因为终止条件是判断叶子节点,所以递归的过程中就不要让空节点进入递归了。
递归函数是有返回值的,如果左右只要有一个递归函数返回true,最后都返回true
class Solution {
public:bool tranversal(TreeNode*root,vector<int>&path,int targetSum){path.push_back(root->val);if(root->left==NULL&&root->right==NULL){int sum=0;for(int i=0;i<path.size();i++){sum+=path[i];}if(sum==targetSum)return true;}bool leftbool=false,rightbool=false;if(root->left){leftbool=tranversal(root->left,path,targetSum);path.pop_back();}if(root->right){rightbool=tranversal(root->right,path,targetSum);path.pop_back();}return (leftbool||rightbool);}bool hasPathSum(TreeNode* root, int targetSum) {vector<int>path;if(root==NULL)return false;return tranversal(root,path,targetSum);}
};106. 从中序与后序遍历序列构造二叉树
题目
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
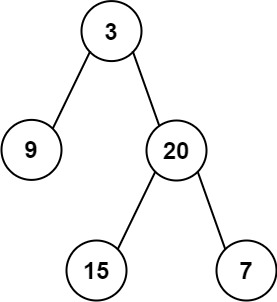
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
题目解析
后序遍历的二叉树数组会有一个特点,所有根节点会在数组的最后,而中序遍历是先遍历左子树再根节点最后右子树。
所以这道题的解题思路就是首先从后序遍历数组取最后一个元素,然后找中序数组中该元素的位置,切割中序数组,此时该元素左边的所有元素值为根节点左子树的值,右边的元素为根节点右子树上的元素。后面不断递归,直到二叉树被构建好。
思路是这么个思路,然后代码实现里还有许多细节需要注意。下面就来说一说:
post_idx:从后向前遍历后序遍历数组
idx_map:<元素值,下标> 方便直接找到后序遍历中的元素值对应在中序遍历数组中的下标
在主函数里将这些定义好后就可以开始递归了
首先看看递归传的参数
一个左,一个右,然后还有两个vector。左右是用来确定子树的范围的,比如所给案例里,root结点的左子树的范围就是0,右子树是2-4。
终止条件
如果子树的范围被压缩得没有了,那么说明此时得这个节点是一个叶子结点,直接返回空就可以
单次递归逻辑
从后序数组里取出对应post_idx位置的元素,在中序数组里找到对应index,然后切割中序数组,左子树的根节点在左边找,右子树的根节点在右边找,然后返回当前节点。
C++代码:
class Solution {int post_idx;unordered_map<int,int>idx_map;
public:TreeNode*helper(int leftindex,int rightindex,vector<int>& inorder, vector<int>& postorder){if (leftindex > rightindex) {return nullptr;}int root_val = postorder[post_idx];TreeNode* root = new TreeNode(root_val);int index=idx_map[root->val];post_idx--;root->right=helper(index+1,rightindex,inorder,postorder);root->left=helper(leftindex,index-1,inorder,postorder);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {post_idx=inorder.size()-1;int idx=0;for(auto&val:inorder){idx_map[val]=idx++;}return helper(0,inorder.size()-1,inorder,postorder);}
};