题目描述：

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

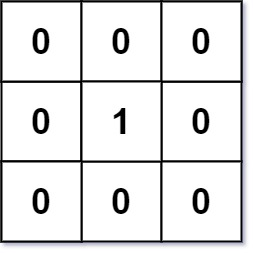
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0 

题目链接：

. - 力扣（LeetCode）

解题主要思路：

这道题明显是bfs的一种，但是跟之前刷到的 "最短路径" 类题目又不太一样。准确的来说，之前刷到的 "最短路径" 类题目是端到端的bfs，而这道题是多个端到一个端的bfs，即多源bfs。如果按照之前的 "最短路径" 的方式来硬解的话，遍历原数组的时间复杂度是On，遍历原数组的时候进行bfs，时间复杂度是On2，这样下来时间复杂度来到了惊人的On的立方。

其实，我们可以换个思路，既然是多个端到一个端，那我们就反着来，从一个端一层一层往外扩到多个端。就以这题为例，多个端指的是1，一个端指的是0，我们就反着来，从0的位置一层一层往外扩。

解题代码：

class Solution {
public:int dx[4]{0, 0, 1, -1};int dy[4]{1, -1, 0, 0};vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int m = mat.size(), n = mat[0].size();vector<vector<int>> ret(m, vector<int>(n, -1));queue<pair<int, int>> que;// 将0的坐标加入到队列中for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) if (mat[i][j] == 0) {que.push(make_pair(i, j));ret[i][j] = 0;}// ret[x][y] == -1 原数组该下标元素为1且未遍历（外扩到）// ret[x][y] != -1 原数组该下标元素为0 or 该位置为1且已遍历// 一层一层往外扩while (que.size()) {auto [a, b] = que.front(); que.pop();for (int i = 0; i < 4; ++i) {int x = a + dx[i], y = b + dy[i];if (x >= 0 && x < m && y >= 0 && y < n && ret[x][y] == -1) {ret[x][y] = ret[a][b] + 1;que.push(make_pair(x, y));}}}return ret;}};