【leetcode练习·二叉树】用「遍历」思维解题 III

本文参考labuladong算法笔记[【强化练习】用「遍历」思维解题 III | labuladong 的算法笔记]

437. 路径总和 III | 力扣 | LeetCode |

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

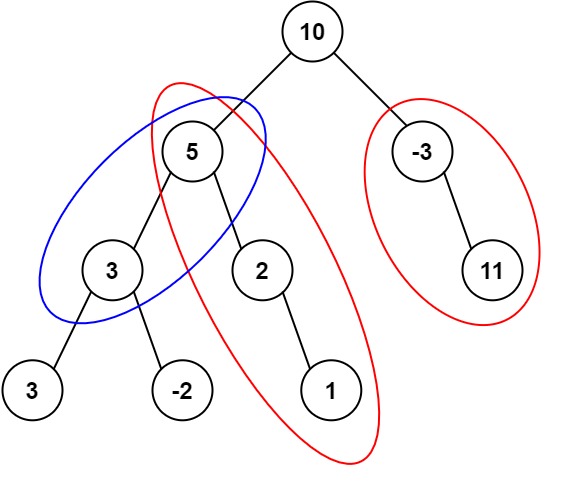
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109
-1000 <= targetSum <= 1000

这题及要求你准确理解二叉树的前序后序遍历，还要熟悉前缀和技巧，把前缀和技巧用到二叉树上。

你可以先看前文前缀和技巧，然后做一下 560. 和为K的子数组，应该能够理解这道题的思路了。

你把二叉树看做是数组，利用前后序遍历来维护前缀和，看下图就能理解解法中几个关键变量的关系了：

class Solution:# 记录前缀和# 定义：从二叉树的根节点开始，路径和为 pathSum 的路径有 preSumCount.get(pathSum) 个def __init__(self):self.preSumCount = {}self.path_sum = 0self.target_sum = 0self.res = 0def pathSum(self, root: TreeNode, targetSum: int) -> int:if root is None:return 0self.path_sum = 0self.target_sum = targetSumself.preSumCount[0] = 1self.traverse(root)return self.resdef traverse(self, root: TreeNode):if root is None:return# 前序遍历位置self.path_sum += root.val# 从二叉树的根节点开始，路径和为 pathSum - targetSum 的路径条数# 就是路径和为 targetSum 的路径条数self.res += self.preSumCount.get(self.path_sum - self.target_sum, 0)# 记录从二叉树的根节点开始，路径和为 pathSum 的路径条数self.preSumCount[self.path_sum] = self.preSumCount.get(self.path_sum, 0) + 1self.traverse(root.left)self.traverse(root.right)# 后序遍历位置self.preSumCount[self.path_sum] = self.preSumCount.get(self.path_sum) - 1self.path_sum -= root.val

513. 找树左下角的值 | 力扣 | LeetCode |

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

输入: root = [2,1,3]
输出: 1

示例 2:

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

二叉树的节点个数的范围是 [1,104]
-231 <= Node.val <= 231 - 1

二叉树递归框架代码是先递归左子树，后递归右子树，所以到最大深度时第一次遇到的节点就是左下角的节点。

class Solution:def __init__(self):# 记录二叉树的最大深度self.maxDepth = 0# 记录 traverse 递归遍历到的深度self.depth = 0self.res = Nonedef findBottomLeftValue(self, root: TreeNode) -> int:self.traverse(root)return self.res.valdef traverse(self, root: TreeNode):if root is None:return# 前序遍历位置self.depth += 1if self.depth > self.maxDepth:# 到最大深度时第一次遇到的节点就是左下角的节点self.maxDepth = self.depthself.res = rootself.traverse(root.left)self.traverse(root.right)# 后序遍历位置self.depth -= 1

1261. 在受污染的二叉树中查找元素 | 力扣 | LeetCode |

给出一个满足下述规则的二叉树：

root.val == 0
如果 treeNode.val == x 且 treeNode.left != null，那么 treeNode.left.val == 2 * x + 1
如果 treeNode.val == x 且 treeNode.right != null，那么 treeNode.right.val == 2 * x + 2

现在这个二叉树受到「污染」，所有的 treeNode.val 都变成了 -1。

请你先还原二叉树，然后实现 FindElements 类：

FindElements(TreeNode* root) 用受污染的二叉树初始化对象，你需要先把它还原。
bool find(int target) 判断目标值 target 是否存在于还原后的二叉树中并返回结果。

示例 1：

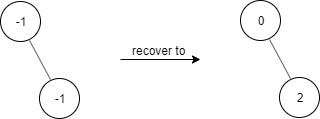
输入：
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
输出：
[null,false,true]
解释：
FindElements findElements = new FindElements([-1,null,-1]); 
findElements.find(1); // return False 
findElements.find(2); // return True

示例 2：

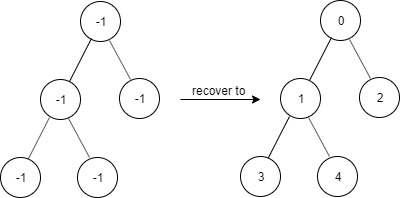
输入：
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
输出：
[null,true,true,false]
解释：
FindElements findElements = new FindElements([-1,-1,-1,-1,-1]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False

示例 3：

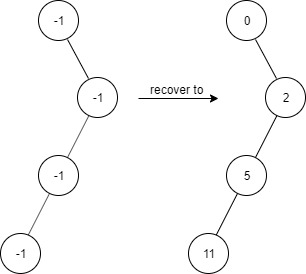
输入：
["FindElements","find","find","find","find"]
[[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]]
输出：
[null,true,false,false,true]
解释：
FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True

提示：

TreeNode.val == -1
二叉树的高度不超过 20
节点的总数在 [1, 10^4] 之间
调用 find() 的总次数在 [1, 10^4] 之间
0 <= target <= 10^6

还原二叉树的时候只需要遍历所有节点，通过函数参数传递每个节点的值；由于节点的个数规模不算大，所以可以直接用一个 HashSet 缓存所有节点值，实现 find 函数的功能。

当然，题目给的这种二叉树节点的取值规律非常像用数组存储完全二叉树的场景，所以你应该可以通过 target 推算出来它在第几层的什么位置，不过我这里就不实现了，类似的题目你可以参考 1104. 二叉树寻路和 662. 二叉树最大宽度。

class FindElements:# 帮助 find 函数快速判断def __init__(self, root):# 还原二叉树中的值self.values = set()self.traverse(root, 0)# 二叉树遍历函数def traverse(self, root, val):if root is None:returnroot.val = valself.values.add(val)self.traverse(root.left, 2 * val + 1)self.traverse(root.right, 2 * val + 2)def find(self, target):return target in self.values

386. 字典序排数 | 力扣 | LeetCode |

给你一个整数 n ，按字典序返回范围 [1, n] 内所有整数。

你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。

示例 1：

输入：n = 13
输出：[1,10,11,12,13,2,3,4,5,6,7,8,9]

示例 2：

输入：n = 2
输出：[1,2]

提示：

1 <= n <= 5 * 104

这个题还挺有意思，要不是它把这道题放在 DFS 的题目分类里面，可能还不太好发现这是一个 DFS 的题目。

它的递归树大概是这样生长的：

首先看 1 这个节点，1 可以生出二位数 10, 11, 12...

其中 10 又可以生出 100, 101, 102...，11 又可以生出 110, 111, 112...

这棵多叉树是不是就出来了？每个节点最多可以生出 10 个节点，这就是一个十叉树。

class Solution:def __init__(self):self.res = []def lexicalOrder(self, n: int) -> List[int]:# 总共有 9 棵多叉树，从 1 开始for i in range(1, 10):self.traverse(i, n)return self.res# 多叉树遍历框架，前序位置收集所有小于 n 的节点def traverse(self, root: int, n: int) -> None:if root > n:returnself.res.append(root)for child in range(root * 10, root * 10 + 10):if child > n:breakself.traverse(child, n)

1104. 二叉树寻路 | 力扣 | LeetCode |

在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点逐行依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

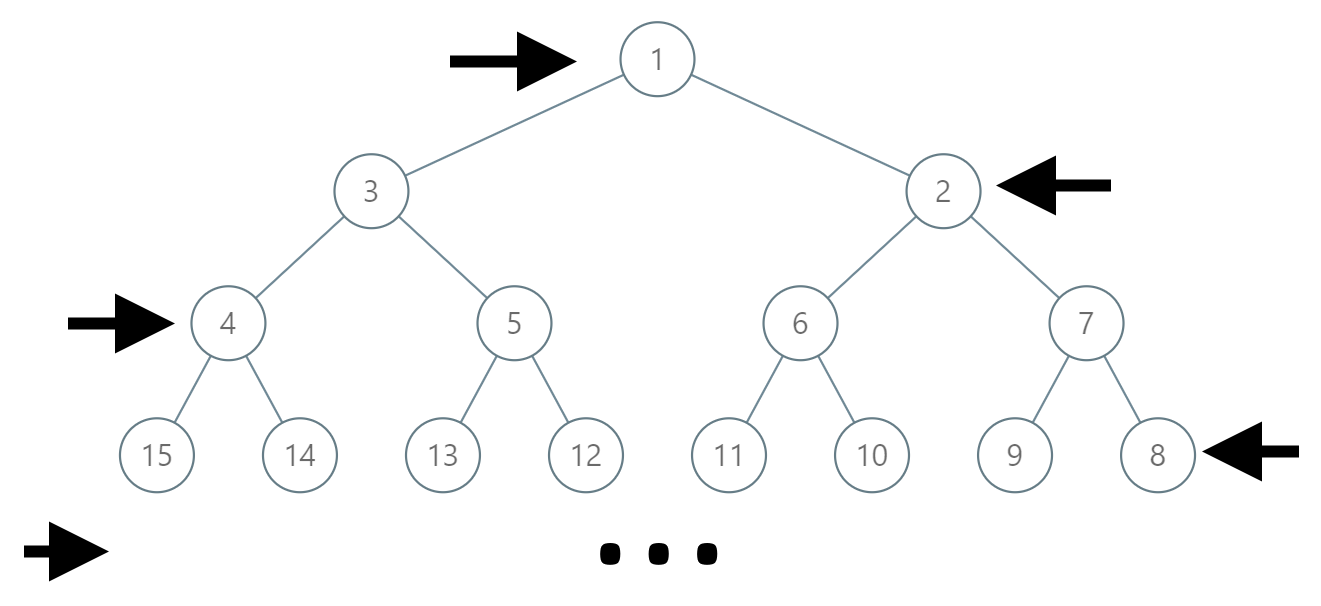
给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

示例 1：

输入：label = 14
输出：[1,3,4,14]

示例 2：

输入：label = 26
输出：[1,2,6,10,26]

提示：

1 <= label <= 10^6

先假设全都是从左到右排列，没有之字形排列的这个条件：

如果我想求到达某一个 label 节点的路径，那么我一直对 label 除以 2 就行了（忽略余数）。

你比如我想求到达 13 的路径，就是 13, 6, 3, 1，然后反转一下就行了。大致的代码逻辑如下：

ArrayList<Integer> path = new ArrayList<>();
while (label >= 1) {path.add(label);label = label / 2;
}
// 反转成从根节点到目标节点的路径
Collections.reverse(path);

现在虽然是之字形排列，但稍加修改就可以适应这个变化：

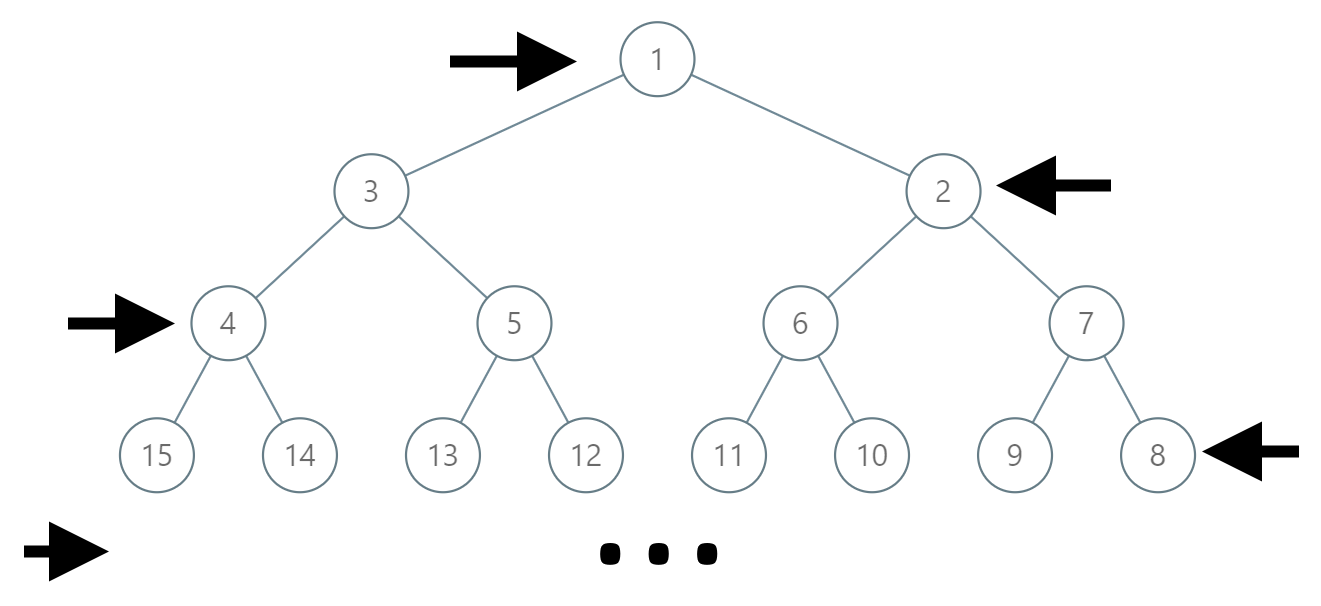
13 的父节点不是 6 了，而是 7 - (6 - 4) = 5。

这个 7 和 4 是哪里来的？就是 6 这一行的最小节点值和最大节点值，而对于完全二叉树，每一行的最大最小值可以通过计算 2 的指数算出来的。

import mathclass Solution:def pathInZigZagTree(self, label: int) -> List[int]:res = []# 对于常规杨辉三角的二叉树，某一节点自身连续除以2，所得值即为该节点到根节点的路径while label > 0:res.append(label)label //= 2# 反转成从根节点到目标节点的路径res.reverse()# 对于“之”字形排列的杨辉三角，label在奇数行和偶数行的效果不一样，需要加以区分label_id = len(res) - 1# 判断label在奇数行还是偶数行is_odd = label_id % 2return self.get_new_val(is_odd, res)# 画个图就容易理解奇数行和偶数行各自的情况了def get_new_val(self, is_odd, res):for id, val in enumerate(res):if id % 2 == 1 - is_odd:max_val = int(math.pow(2, id+1)) - 1min_val = int(math.pow(2, id))# 由于该行可能被翻转，则需要找到翻转后对应的值res[id] = min_val + max_val - valreturn res

1145. 二叉树着色游戏 | 力扣 | LeetCode |

有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中，给出二叉树的根节点 root，树上总共有 n 个节点，且 n 为奇数，其中每个节点上的值从 1 到 n 各不相同。

最开始时：

「一号」玩家从 [1, n] 中取一个值 x（1 <= x <= n）；
「二号」玩家也从 [1, n] 中取一个值 y（1 <= y <= n）且 y != x。

「一号」玩家给值为 x 的节点染上红色，而「二号」玩家给值为 y 的节点染上蓝色。

之后两位玩家轮流进行操作，「一号」玩家先手。每一回合，玩家选择一个被他染过色的节点，将所选节点一个 未着色 的邻节点（即左右子节点、或父节点）进行染色（「一号」玩家染红色，「二号」玩家染蓝色）。

如果（且仅在此种情况下）当前玩家无法找到这样的节点来染色时，其回合就会被跳过。

若两个玩家都没有可以染色的节点时，游戏结束。着色节点最多的那位玩家获得胜利 ✌️。

现在，假设你是「二号」玩家，根据所给出的输入，假如存在一个 y 值可以确保你赢得这场游戏，则返回 true ；若无法获胜，就请返回 false 。

示例 1 ：

输入：root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
输出：true
解释：第二个玩家可以选择值为 2 的节点。

示例 2 ：

输入：root = [1,2,3], n = 3, x = 1
输出：false

提示：

树中节点数目为 n
1 <= x <= n <= 100
n 是奇数
1 <= Node.val <= n
树中所有值 互不相同

基本思路

这道题的关键是要观察规律，根据游戏规则，对方先选一个节点之后，你的最优策略就是紧贴着对方的那个节点选择，也就是说你应该选择节点 x 的左右子节点或者父节点。

做出以上三种选择，你可以占据二叉树的不同部分，如下图：

你如果想赢，必须占据超过 n / 2 的节点，也就是说，如果这三个蓝色区域中节点数最多的那个区域中的节点个数大于 n / 2，你能赢，否则你就输。

所以本题转化为计算二叉树节点个数的简单问题。

class Solution:def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:node = self.find(root, x)left_count = self.count(node.left)right_count = self.count(node.right)other_count = n - 1 - left_count - right_countreturn max(left_count, max(right_count, other_count)) > n // 2# 定义：在以 root 为根的二叉树中搜索值为 x 的节点并返回def find(self, root: TreeNode, x: int) -> TreeNode:if root is None:return Noneif root.val == x:return root# 去左子树找left = self.find(root.left, x)if left is not None:return left# 左子树找不到的话去右子树找return self.find(root.right, x)# 定义：计算以 root 为根的二叉树的节点总数def count(self, root: TreeNode) -> int:if root is None:return 0return 1 + self.count(root.left) + self.count(root.right)

1612. 检查两棵二叉表达式树是否等价 | 力扣 | LeetCode |

二叉表达式树是一种表达算术表达式的二叉树。二叉表达式树中的每一个节点都有零个或两个子节点。叶节点（有 0 个子节点的节点）表示操作数，非叶节点（有 2 个子节点的节点）表示运算符。在本题中，我们只考虑 '+' 运算符（即加法）。

给定两棵二叉表达式树的根节点 root1 和 root2 。如果两棵二叉表达式树等价，返回 true ，否则返回 false 。

当两棵二叉搜索树中的变量取任意值，分别求得的值都相等时，我们称这两棵二叉表达式树是等价的。

示例 1:

输入： root1 = [x], root2 = [x]
输出： true

示例 2:

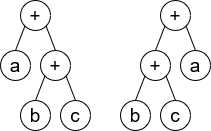
输入：root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,c]
输出：true
解释：a + (b + c) == (b + c) + a

示例 3:

输入： root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,d]
输出： false
解释： a + (b + c) != (b + d) + a

提示：

两棵树中的节点个数相等，且节点个数为范围 [1, 4999] 内的奇数。
Node.val 是 '+' 或小写英文字母。
给定的树保证是有效的二叉表达式树。

进阶：当你的答案需同时支持 '-' 运算符（减法）时，你该如何修改你的答案

题目说算式中只有加号，所以判断两个算式是否相同，只需要分别遍历两棵二叉树，判断两棵二叉树中的未知数数量是否相同即可。

有了这个思路就很容易写出解法了，我们可以用一个小技巧，用 count 数组当做计数器，对第一棵树上的元素 +1，对第二棵树上的元素 -1，这样一来，只要最终 count 数组中全是 0 就说明两棵树上的未知数数量相同。

class Solution:def checkEquivalence(self, root1: 'Node', root2: 'Node') -> bool:# 给 root1 的未知数计数self.traverse(root1, 1)# 给 root2 的未知数计数self.traverse(root2, -1)# 如果等价，未知数的数量应该相同for f in self.count:if f != 0:return Falsereturn True# 记录未知数def __init__(self):self.count = [0] * 26# 二叉树遍历函数def traverse(self, root: 'Node', delta: int):if root is None:return# 改变未知数的个数if 'a' <= root.val <= 'z':self.count[ord(root.val) - ord('a')] += deltaself.traverse(root.left, delta)self.traverse(root.right, delta)

572. 另一棵树的子树 | 力扣 | LeetCode |

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

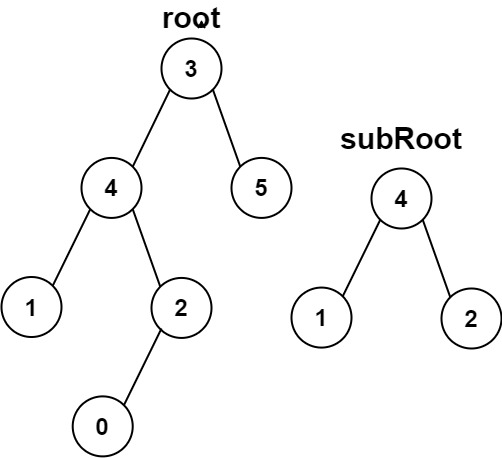
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

提示：

root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104

遍历以 root 为根的这棵二叉树的所有节点，用 100. 相同的树中的 isSame 函数判断以该节点为根的子树是否和以 subRoot 为根的那棵树相同。

class Solution:def isSubtree(self, root: TreeNode, subRoot: TreeNode) -> bool:if root is None:return subRoot is None# 判断以 root 为根的二叉树是否和 subRoot 相同if self.isSameTree(root, subRoot):return True# 去左右子树中判断是否有和 subRoot 相同的子树# 妙就妙在中间这个 or !!! 因为它只要左子树或右子树其一包含即可return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:# 判断一对节点是否相同，经典判断两棵二叉树是否相等的代码if p is None and q is None:return Trueif p is None or q is None:return Falseif p.val != q.val:return False# 判断其他节点是否相同return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

1367. 二叉树中的链表 | 力扣 | LeetCode |

给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。

如果在二叉树中，存在一条一直向下的路径，且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值，那么请你返回 True ，否则返回 False 。

一直向下的路径的意思是：从树中某个节点开始，一直连续向下的路径。

示例 1：

输入：head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：true
解释：树中蓝色的节点构成了与链表对应的子路径。

示例 2：

输入：head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：true

示例 3：

输入：head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：false
解释：二叉树中不存在一一对应链表的路径。

提示：

二叉树和链表中的每个节点的值都满足 1 <= node.val <= 100 。
链表包含的节点数目在 1 到 100 之间。
二叉树包含的节点数目在 1 到 2500 之间。

本质上，isSubPath 就是在遍历二叉树的所有节点，对每个节点用 check 函数判断是否能够将链表嵌进去。

class Solution:def isSubPath(self, head: ListNode, root: TreeNode) -> bool:# base caseif head is None:return Trueif root is None:return False# 当找到一个二叉树节点的值等于链表头结点时if head.val == root.val:# 判断是否能把链表嵌进去if self.check(head, root):return True# 继续去遍历其他节点尝试嵌入链表，妙就妙在这个 or !!!return self.isSubPath(head, root.left) or self.isSubPath(head, root.right)# 检查是否能够将链表嵌入二叉树def check(self, head: ListNode, root: TreeNode) -> bool:if head is None:return Trueif root is None:return Falseif head.val == root.val:# 在子树上嵌入子链表return self.check(head.next, root.left) or self.check(head.next, root.right)return False