一、实验目的
掌握有关非线性回归的理论知识,通过变量代换把本来应该用非线性回归处理的问题近似转化为线性回归问题,并进行分析预测。
二、实验任务
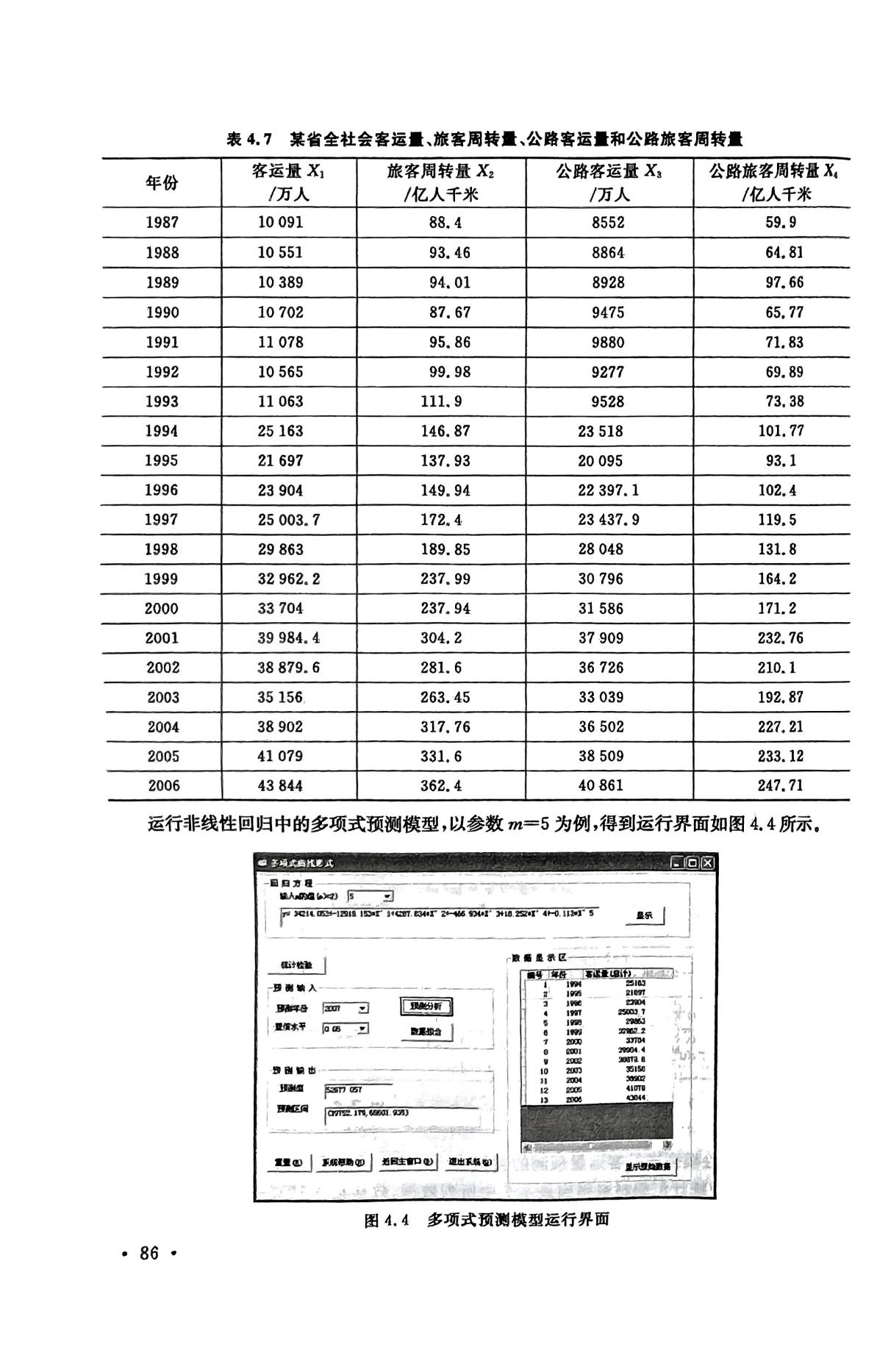
对非线性回归实例进行编码计算,实例如下:

三、实验过程
1.运行非线性回归中的多项式预测模型,以参数m=5为例进行预测
2.对多项式预测模型进行统计检验
3.进行数据拟合,观察预测模型对原始数据的拟合结果
4.对表中客运量和旅客周转量、公路客运量和公路旅客周转量数据分别进行运算,得到非线性回归曲线方程表
四、实验结果
实现平台:Matlab 2022A
实验代码:
①多项式预测模型
% 年份和客运量的数据
years = 1987:2006;
passengers = [10091,10551,10389,10702,11078,10565,11063,25163,21697,23904,25003.7,29863,32962.2,33704,39984.4,38879.6,35156,38902,41079,43844];% 将年份和客运量数据进行多项式拟合
degree = 5; % 多项式的阶数
coefficients = polyfit(years, passengers, degree);
% 创建一个新的年份序列,用于预测
new_years = 1987:0.1:2007; % 以生成一个新的年份序列,注意:第三个值是你要预测的年份% 使用 polyval 函数计算预测的客运量
predicted_passengers = polyval(coefficients, new_years);% 绘制原始数据和预测结果
plot(years, passengers, 'o', new_years, predicted_passengers, '-');
xlabel('年份');
ylabel('客运量');
title('年份与客运量的多项式预测');
legend('原始数据', '预测结果');% 拟合优度检验
y_mean = mean(passengers);
SS_total = sum((passengers - y_mean).^2);
SS_residual = sum((passengers - polyval(coefficients, years)).^2);
R2 = 1 - SS_residual / SS_total;% F检验
n = length(passengers);
m = degree + 1; % 多项式阶数加上常数项
F = (SS_total - SS_residual) / (SS_residual / (n - m));
alpha = 0.05; % 显著性水平
F_critical = finv(1 - alpha, m, n - m); % 计算临界值% 打印结果
fprintf('拟合优度检验结果:\n');
fprintf('拟合优度(R^2)= %.4f\n', R2);fprintf('\nF检验结果:\n');
fprintf('F统计量 = %.4f\n', F);
if F > F_criticalfprintf('多项式拟合模型具有显著性\n');
elsefprintf('多项式拟合模型不具有显著性\n');
end% 打印预测模型
fprintf('预测模型:\n');
fprintf('客运量 = ');
for i = 1:degreefprintf('%.4f * 年份^%d + ', coefficients(i), degree+1-i);
end
fprintf('%.4f\n', coefficients(degree+1));
②幂函数预测模型
% 输入数据
years = 1987:2006;
passengers = [10091,10551,10389,10702,11078,10565,11063,25163,21697,23904,25003.7,29863,32962.2,33704,39984.4,38879.6,35156,38902,41079,43844];% 拟合幂函数模型
f = fittype('a * x^b'); % 定义幂函数模型
model = fit(years.', passengers.', f); % 拟合模型% 显示拟合结果
disp(model);% 绘制拟合曲线
plot(model, years, passengers,'o');
hold on; % 保持图形,添加预测结果
xlabel('年份');
ylabel('客运量');
title('幂函数拟合结果');% 进行预测
future_years = 2007; % 要预测的未来年份
predicted_passengers = model(future_years); % 预测客运量% 显示预测结果
disp('未来年份的客运量预测:');
disp([future_years; predicted_passengers].');% 将预测结果画在图上
plot(future_years, predicted_passengers, 'ro', 'MarkerSize',5); % 使用红色圆点标记预测结果
legend('已知数据', '拟合曲线', '预测结果');
hold off; % 结束图形保持实验结果:
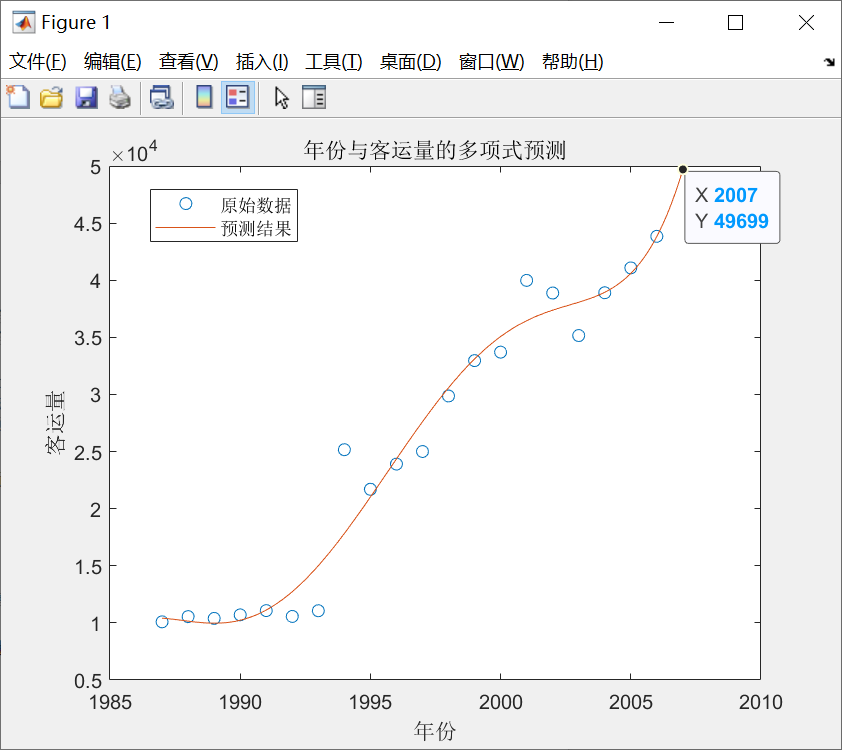
1.运行非线性回归中的多项式预测模型,以参数m=5为例进行预测
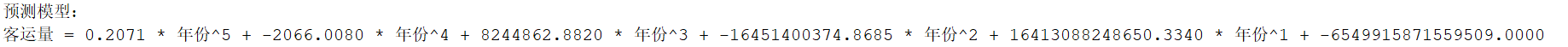
2.对多项式预测模型进行统计检验

3.进行数据拟合,观察预测模型对原始数据的拟合结果
4.改用幂函数模型,再次进行预测

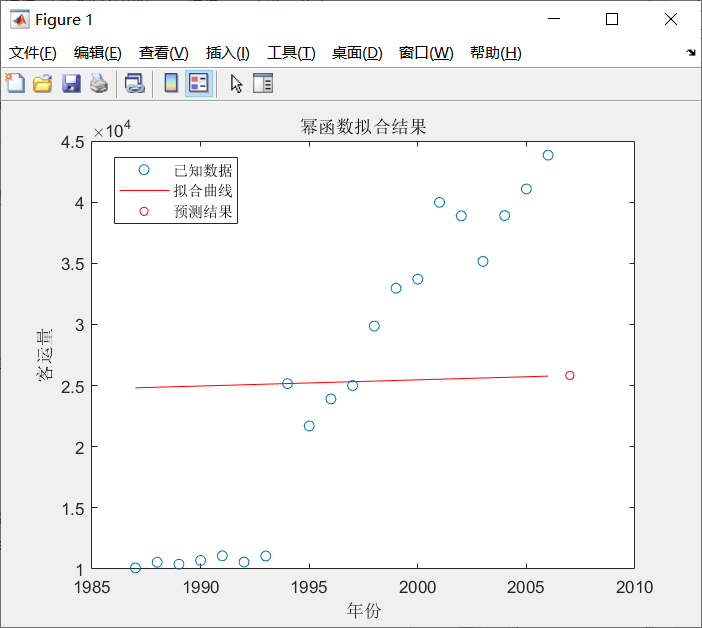
五、个人总结
1.对非线性回归预测模型的理解
在实际问题中,非常多的变量之间都是非线性关系,我们可以通过变量代换将本来是非线性关系的问题近似地转化成线性关系,再进行分析预测。在非线性回归模型中,因变量与自变量的关系可以是曲线、指数、对数等非线性形式,而不是线性形式。
2.对编码实现过程的回顾
这个代码的实现用到了许多matlab当中特有的数学函数,在编写代码的过程当中我查阅了很多资料,以下为一部分实现此实验用到的特殊函数:
①polyfit多项式曲线拟合函数
p = polyfit(x,y,n)返回次数为 n 的多项式 p(x) 的系数,该阶数是 y 中数据的最佳拟合(基于最小二乘指标)。p 中的系数按降幂排列,p 的长度为 n+1
②polyval多项式计算函数
y = polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量,其元素是 n 次多项式的系数(降幂排序)
③fittype曲线和曲面拟合的拟合类型
这个函数有很多用法,详见matlab帮助中心,这里只列出我使用的一种
aFittype = fittype(linearModelTerms) 使用 linearModelTerms 中的表达式指定的项为自定义线性模型创建拟合类型