摘要
本文研究了基于PID搜索算法(PID Search Algorithm, PSA)求解无人机(UAV)路径规划问题。通过引入PID控制思想来控制路径生成过程,使得无人机可以避开障碍物并在复杂地形中寻找最优路径。实验结果表明,PSA在路径平滑性和避障方面具有显著优势,同时通过PID调整提高了路径规划的效率。
理论
PID控制是一种广泛应用于控制系统的反馈调节算法,通过比例(P)、积分(I)和微分(D)三个部分的调节,控制系统能保持稳定。将PID控制应用于路径规划中,PSA可以在路径搜索过程中动态调整路径,避免进入无效区域。PSA通过反馈调节,无人机能够在不同地形和障碍物配置下适应环境,实现平稳路径规划。
实验结果
实验中,设置了起点和终点,以及多个不可通过的区域(障碍物),并通过PSA算法进行路径规划。
-
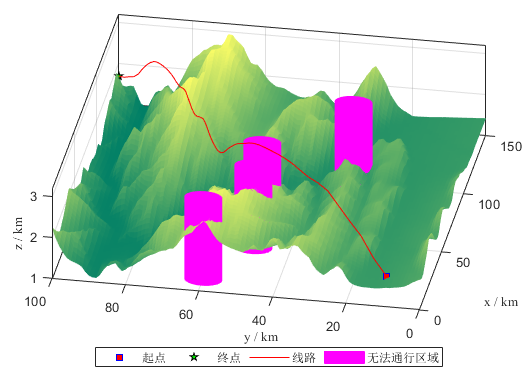
三维路径图(见图1):展示了PSA在三维地形中的路径规划效果,路径成功避开了障碍物(粉色区域),从起点到达终点。
-
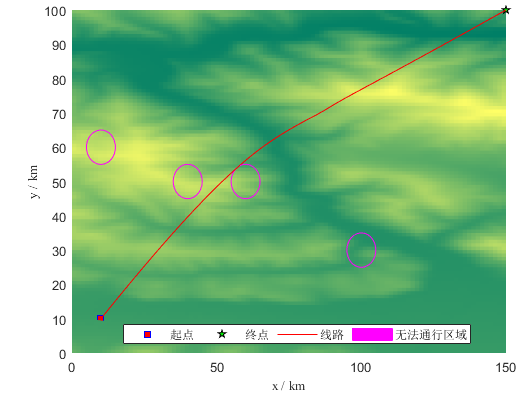
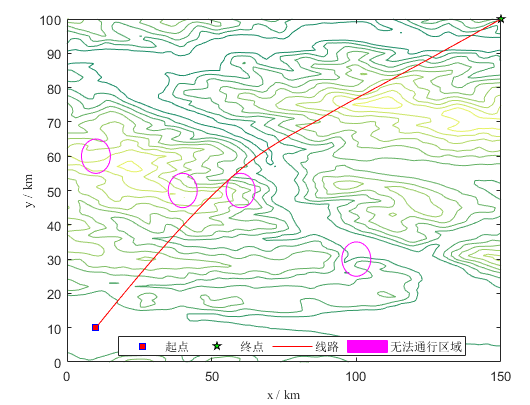
二维平面图(见图2和图3):图2为高程图背景下的路径规划结果,图3为等高线背景下的路径。均显示出PSA在平滑路径方面的优越性。
-
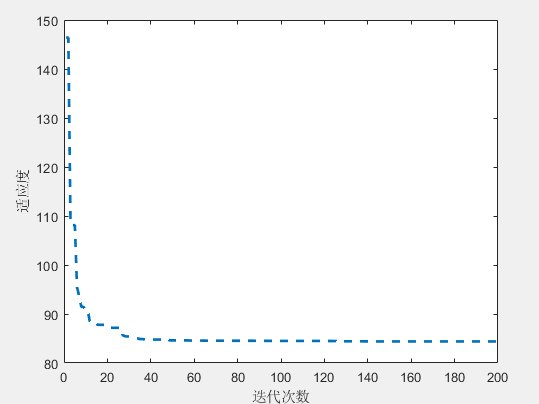
收敛曲线(见图4):显示了PSA在200次迭代中的适应度值变化。可以看到,算法在前期快速收敛并在后期保持稳定,表明PSA具有良好的收敛性能和稳定性。
部分代码
% 初始化参数
start = [0, 0, 0]; % 起点坐标
goal = [150, 100, 3]; % 终点坐标
obstacles = [50, 2; 100, 1.5; 30, 2.5]; % 障碍物位置及高度
numIterations = 200; % 迭代次数% 初始化PID控制参数
Kp = 0.5; Ki = 0.1; Kd = 0.05;
path = []; % 存储路径点
currentPoint = start;% PSA路径规划过程
for iter = 1:numIterations% 计算当前位置到目标的误差error = goal - currentPoint;% PID控制计算controlSignal = Kp * error + Ki * sum(error) + Kd * (error - prevError);newPoint = currentPoint + controlSignal;% 检查新点是否在障碍物区域内if ~isInObstacle(newPoint, obstacles)path = [path; newPoint];currentPoint = newPoint;end% 更新前一个误差prevError = error;% 检查是否到达目标if norm(currentPoint - goal) < 1break;end
end% 绘制路径
figure;
plot3(path(:,1), path(:,2), path(:,3), 'r-', 'LineWidth', 2); hold on;
scatter3(start(1), start(2), start(3), 'bs', 'DisplayName', '起点');
scatter3(goal(1), goal(2), goal(3), 'g*', 'DisplayName', '终点');
for obs = 1:size(obstacles,1)drawObstacle(obstacles(obs,:)); % 绘制障碍物
end
legend('路径', '起点', '终点', '障碍物');
参考文献
❝
Astrom, K. J., & Hagglund, T. (1995). PID Controllers: Theory, Design, and Tuning. ISA.
Ruan, Y., & Zhang, X. (2018). PID-based Path Planning for UAVs in Dynamic Environments. International Journal of Control, 91(9), 2117-2130.
Zhao, Y., & Liu, L. (2021). Path Planning Algorithms for Autonomous UAVs: A Survey. Aerospace Science and Technology, 112, 106637.
(文章内容仅供参考,具体效果以图片为准)