三维测量与建模笔记 - 特征提取与匹配 - 4.2 梯度算子、Canny边缘检测、霍夫变换直线检测

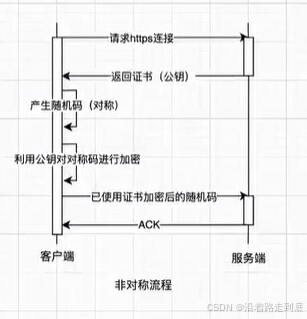
从Roberts交叉算子的卷积核可以看出，它实际计算了对角线上元素之间的差值。

prewitt算子实际是对整行或整列、或者对角线两侧的像素进行差分计算。

Sobel算子改进了一下Prewitt算子，增加了权重，中心位置的像素权重为2。

中心权重为4的Laplacian算子，计算的是梯度。权重为9的算子加上了对角线的像素，此时的效果相当于是对得到的梯度值进行了增强（Laplacian锐化模版）。

下图展示了不同算子对同一副图像进行计算后的结果对比：

非极大值抑制，可以简单理解为沿着某个方向进行搜索，只保留最大值，目的是找出候选的边缘像素点。

双阈值是指有两个值，大于高阈值的标记为强边缘；小于低阈值标记为非边缘，被抑制，如果是两者之间就标记为弱边缘。

第五步实际是对弱边缘进行进一步处理，找出可能是真实边缘的弱边缘。

直线方程通用式是ax+by+c = 0，除去这三种方式表示直线外，还有法线式表示：

法线式就是霍夫直线检测所使用的形式，上式中 $\rho$ 表示的是直线对应的法线。根据正弦和余弦公式，可以得到两个截距a,b和 $\rho, \theta$ 的关系，代换回截距式可以推导出法线式。

首先我们来看一些基本概念：

在图像空间（x,y轴组成的平面）中，将直线上的点x,y称为变量，直线的斜率m和截距b称为参数。

如果将图像空间切换到参数空间（以m和b为基础坐标系的空间），此时x,y成了参数，m,b是变量（比如已知b求m）。此时图像空间上的一条直线，在参数空间下就变成了一个点。

回到直线方程的法线式表示中，图像空间中的一条直线，在 $\rho, \theta$ 的空间中，也是一个点。

假设图像空间中有一条直线，直线上有一点(x0,y0),这个点在参数空间中对应是一条曲线（简单理解就是法线式中已知量是 x, y, 需要找到满足方程 $x_0cos\theta + y_0sin\theta = \rho$ 的 $\rho, \theta$ ，这些 $\rho, \theta$ 的集合从图形上看是一条曲线）。如果我们在图像空间中已知两点(x1,y1),(x2,y2),则在参数空间中对应两条曲线（下图中r就是 $\rho$ ）：

有了上面的概念后，我们接着来看霍夫变换检测直线的原理。首先，在图像空间上进行边缘检测(比如Canny边缘检测)，得到了边缘信息的图像。取出边缘像素的位置，将其映射到参数空间中，可以得到多条直线。如果边缘像素在同一条直线上，则这些像素在参数空间对应的多条曲线上必定有一个交点。

如上图所示，图像空间中两个蓝色点、一个橙色点在一条直线上，褐色点不在一条直线上，则对应参数空间中，有三条曲线交于一个公共点，有一条曲线则顶多和某一条直线在某个位置有交点，不会通过前面三条线的公共点。

下图更为直观地展示了在图像空间中有一系列的点在一条直线上，在参数空间中这些曲线有一个公共的交点。

下面是一个霍夫直线检测的算法的流程描述（图中的d是 $\rho$ ）：

实际过程很直白，第一步是初始化H空间（ $\rho, \theta$ ）数组，所有元素值初始为0，表示有0条曲线通过该点。

第二步是对图像空间中的边缘点进行迭代，找到对应曲线经过的H空间坐标，对应坐标的统计数加1。

第三步是找到H空间中拥有局部最大值的点的坐标，这里可以设置一个阈值，比如程序要求大于20个像素在直线上才算检测到（对应就是H空间中某个元素的值大于20）。

最后代换 $\rho, \theta$ 回法线式的直线方程得到图像空间中的直线。

关于霍夫直线检测，更详细的内容可以参考如下链接：

霍夫变换直线检测（Line Detection）原理及示例_霍夫变换直线检测原理-CSDN博客文章浏览阅读10w+次，点赞368次，收藏1.1k次。霍夫变换直线检测（Line Detection）原理及示例微信公众号：幼儿园的学霸个人的学习笔记，关于OpenCV,关于机器学习, … 问题或建议，请公众号留言;给定一幅图像（一般为二值图像）中的点集合，如何检测直线？一种解决方法：任选一对点，决定一条线，然后测试所有其他点是否接近这条线，从而得出接近这条特殊线的所有点的子集。该方法比较复杂。另外一种方法便是采用霍夫变换。霍夫变换是图..._霍夫变换直线检测原理https://blog.csdn.net/leonardohaig/article/details/87907462