前缀和技巧解析
前缀和(Prefix Sum)是一种常用的算法技巧,用于高效地处理一系列连续子数组和的问题。通过构建一个额外的数组来存储从数组起始位置到当前位置的累计和,可以在常数时间内快速计算任意区间的和。
前缀和应用的典型问题
- 区间和查询: 前缀和最常见的应用是快速求解数组中某个区间的和。这对于处理大量的区间和查询非常高效。
- 求子数组的和: 使用前缀和可以快速求解子数组的和。
- 二维矩阵求和: 前缀和技巧也可以扩展到二维矩阵,方便处理多次查询矩阵子区域的和。
303. 区域和检索 - 数组不可变
给定一个整数数组 nums,处理以下类型的多个查询:
- 计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right
实现 NumArray 类:
NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])
示例 1:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
class NumArray {
public:NumArray(vector<int>& nums) {numsum.resize(nums.size()+1);numsum[0]=0;for(int i=0; i<nums.size(); i++){numsum[i+1]=numsum[i]+nums[i];}}int sumRange(int left, int right) {return (numsum[right+1]-numsum[left]);}
private:vector<int> numsum;
};
304. 二维区域和检索 - 矩阵不可变
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。
实现 NumMatrix 类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。
示例 1:
输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
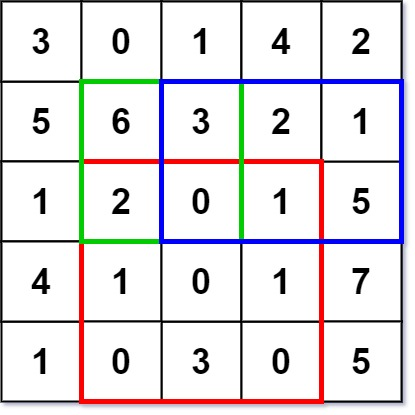
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
思路:构建前缀和矩阵(m+1)*(n+1),因为这个矩阵的第一行和第一列全是0,目的是方便计算
sumnum[i][j]=matrix[i-1][j-1]+sumnum[i-1][j]+sumnum[i][j-1]-sumnum[i-1][j-1];

class NumMatrix {
public:NumMatrix(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();sumnum.resize(m+1 , vector<int>(n+1,0));for(int i=1; i<=m; i++){for(int j=1; j<=n; j++){sumnum[i][j]=matrix[i-1][j-1]+sumnum[i-1][j]+sumnum[i][j-1]-sumnum[i-1][j-1];}}}int sumRegion(int row1, int col1, int row2, int col2) {return sumnum[row2+1][col2+1]-sumnum[row2+1][col1]-sumnum[row1][col2+1]+sumnum[row1][col1];}
private:vector<vector<int>> sumnum;
};
1314. 矩阵区域和
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
i - k <= r <= i + k,j - k <= c <= j + k且(r, c)在矩阵内。
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出:[[45,45,45],[45,45,45],[45,45,45]]
思路:这道题可以直接套用304. 二维区域和检索 - 矩阵不可变 时实现的 NumMatrix 类,主要注意下通过 min, max 函数优雅避免索引越界的技巧。
class Solution {
public:vector<vector<int>> numsum;void numMatrix(vector<vector<int>>& mat){int m = mat.size();int n = mat[0].size();numsum.resize(m+1, vector<int>(n+1,0));for(int i=1; i<=m; i++){for(int j=1; j<=n; j++){numsum[i][j]=mat[i-1][j-1]+numsum[i-1][j]+numsum[i][j-1]-numsum[i-1][j-1];}}}int sumNumlr(int r1, int c1, int r2, int c2){return numsum[r2+1][c2+1]-numsum[r1][c2+1]-numsum[r2+1][c1]+numsum[r1][c1];}vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {numMatrix(mat);int m = mat.size();int n = mat[0].size();vector<vector<int>> answer(m,vector<int>(n,0));for(int i=0; i<m; i++){for(int j=0; j<n; j++){int minr=max(i-k,0);int minc=max(j-k,0);int maxr=min(i+k,m-1);int maxc=min(j+k,n-1);answer[i][j]=sumNumlr(minr, minc, maxr, maxc);}}return answer;}
};
724. 寻找数组的中心下标
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:nums = [1, 7, 3, 6, 5, 6]
输出:3
解释:
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1]
输出:0
解释:
中心下标是 0 。
左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> numsum(n+1, 0);for(int i=1; i<=n; i++){numsum[i] = numsum[i-1] + nums[i-1]; }for(int i=1; i<=n; i++){int leftsum = numsum[i-1];int rightsum = numsum[n]-numsum[i];if(leftsum==rightsum){return i-1;}}return -1;}
};
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 **不要使用除法,**且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
思路:整2个数组,一个是前缀积,一个是后缀积,所求answer元素就是对应前缀积和后缀积的乘积之和
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> qian(n);vector<int> hou(n);vector<int> result(n);qian[0]=nums[0];hou[n-1]=nums[n-1];for(int i=1; i<n; i++){qian[i]=qian[i-1]*nums[i];}for(int i=n-2; i>=0; i--){hou[i]=hou[i+1]*nums[i];}result[0]=hou[1];result[n-1]=qian[n-2];for(int i=1; i<n-1; i++){result[i]=qian[i-1]*hou[i+1];}return result;}
};
1352. 最后 K 个数的乘积
请你实现一个「数字乘积类」ProductOfNumbers,要求支持下述两种方法:
1. add(int num)
- 将数字
num添加到当前数字列表的最后面。
2. getProduct(int k)
- 返回当前数字列表中,最后
k个数字的乘积。 - 你可以假设当前列表中始终 至少 包含
k个数字。
题目数据保证:任何时候,任一连续数字序列的乘积都在 32-bit 整数范围内,不会溢出。
示例:
输入:
["ProductOfNumbers","add","add","add","add","add","getProduct","getProduct","getProduct","add","getProduct"]
[[],[3],[0],[2],[5],[4],[2],[3],[4],[8],[2]]输出:
[null,null,null,null,null,null,20,40,0,null,32]解释:
ProductOfNumbers productOfNumbers = new ProductOfNumbers();
productOfNumbers.add(3); // [3]
productOfNumbers.add(0); // [3,0]
productOfNumbers.add(2); // [3,0,2]
productOfNumbers.add(5); // [3,0,2,5]
productOfNumbers.add(4); // [3,0,2,5,4]
productOfNumbers.getProduct(2); // 返回 20 。最后 2 个数字的乘积是 5 * 4 = 20
productOfNumbers.getProduct(3); // 返回 40 。最后 3 个数字的乘积是 2 * 5 * 4 = 40
productOfNumbers.getProduct(4); // 返回 0 。最后 4 个数字的乘积是 0 * 2 * 5 * 4 = 0
productOfNumbers.add(8); // [3,0,2,5,4,8]
productOfNumbers.getProduct(2); // 返回 32 。最后 2 个数字的乘积是 4 * 8 = 32
class ProductOfNumbers {
public:vector<int> numlist;ProductOfNumbers() {numlist.push_back(1);}void add(int num) {if(num==0){numlist.clear();numlist.push_back(1);return;}int n = numlist.size();numlist.push_back(numlist[n-1]*num);}int getProduct(int k) {int n = numlist.size();if(k>n-1){return 0;}return numlist[n-1]/numlist[n-1-k];}
};525. 连续数组
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1:
输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2:
输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。
**思路:**我们可以通过 前缀和 来转换问题,并利用 哈希表 来记录前缀和的索引。具体步骤如下:
- 前缀和的定义:遍历数组时,我们可以将 0 和 1 转换为两个不同的值,例如,将 0 视为 -1,将 1 视为 +1。这样问题就转化为:找出和为 0 的最长子数组。因为相同数量的 0 和 1 等价于和为 0 的子数组。
- 前缀和的累加:遍历数组时,计算当前元素的前缀和。如果当前前缀和出现过,那么当前子数组与第一次出现该前缀和的索引之间的子数组就含有相同数量的 0 和 1,长度可以计算出来。
- 哈希表的作用:哈希表用于记录每个前缀和第一次出现的位置。哈希表的键是前缀和的值,值是该前缀和第一次出现的位置索引。
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int,int> map;int presum=0;int maxlength=0;map[0]=-1;//i-(-1)=i+1for(int i=0; i<nums.size(); i++){presum += (nums[i]==1)?1:-1;if(map.find(presum)!=map.end()){maxlength=max(maxlength, i-map[presum]);}else{map[presum]=i;}}return maxlength;}
};
523. 连续的子数组和
给你一个整数数组 nums 和一个整数 k ,如果 nums 有一个 好的子数组 返回 true ,否则返回 false:
一个 好的子数组 是:
- 长度 至少为 2 ,且
- 子数组元素总和为
k的倍数。
注意:
- 子数组 是数组中 连续 的部分。
- 如果存在一个整数
n,令整数x符合x = n * k,则称x是k的一个倍数。0始终 视为k的一个倍数。
示例 1:
输入:nums = [23,2,4,6,7], k = 6
输出:true
解释:[2,4] 是一个大小为 2 的子数组,并且和为 6 。
示例 2:
输入:nums = [23,2,6,4,7], k = 6
输出:true
解释:[23, 2, 6, 4, 7] 是大小为 5 的子数组,并且和为 42 。
42 是 6 的倍数,因为 42 = 7 * 6 且 7 是一个整数。
示例 3:
输入:nums = [23,2,6,4,7], k = 13
输出:false
class Solution {
public:bool checkSubarraySum(vector<int>& nums, int k) {//(sumNums[i]-sumNums[j])%k=0 && i-j>=2unordered_map<int,int> map;int presum=0;map[0]=-1;for(int i=0;i<nums.size();i++){presum+=nums[i];int mod=presum%k;if(map.find(mod)!=map.end()){if(i-map[mod]>1){return true;}}else{map[mod]=i;}}return false;}
};
代码解释:
前缀和:我们通过变量 presum 记录到当前位置为止的元素和。
模运算:每次计算 presum % k 来查找之前是否存在相同的模值。如果存在,说明当前的子数组和是 k 的倍数。
哈希表 map:记录每个 presum % k 的首次出现位置。特别地,map[0] = -1 是为了处理从数组开始的子数组(如果前缀和直接就是 k 的倍数)。
返回条件:当我们找到一个符合条件的子数组时,立即返回 true,否则继续遍历。
560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2
示例 2:
输入:nums = [1,2,3], k = 3
输出:2
class Solution {
public:int subarraySum(vector<int>& nums, int k) {//sumNum[i]-sumNum[j]=k && count++unordered_map<int,int> map;int sumNum=0;int count=0;map[0]=1;for(int i=0; i<nums.size(); i++){sumNum+=nums[i];int cha = sumNum-k;if(map.find(cha)!=map.end()){count+=map[cha];}map[sumNum]++;}return count;}
};
974. 和可被 K 整除的子数组
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的非空 子数组 的数目。
子数组 是数组中 连续 的部分。
示例 1:
输入:nums = [4,5,0,-2,-3,1], k = 5
输出:7
解释:
有 7 个子数组满足其元素之和可被 k = 5 整除:
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:
输入: nums = [5], k = 9
输出: 0
//有几种 i、j 组合,满足 (sumNum[j]−sumNum[i−1]) mod K==0。
//有几种 i、j 组合,满足 sumNum[j] mod K == sumNum[i−1] mod K。
//前提:sumNum[j] 、sumNum[i−1] 为正整数。负数的情况要处理
class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {// (sumNum[i]-sumNum[j])%k=0unordered_map<int,int> map;int sumNum = 0;int count = 0;map[0]=1;for(int i=0; i<nums.size(); i++){sumNum+=nums[i];int mod = sumNum%k;if (mod < 0) mod += k;//前缀和取余数不能为负数if(map.find(mod)!=map.end()){count+=map[mod];}map[mod]++;}return count;}
};
1124. 表现良好的最长时间段
给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。
我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
示例 1:
输入:hours = [9,9,6,0,6,6,9]
输出:3
解释:最长的表现良好时间段是 [9,9,6]。
示例 2:
输入:hours = [6,6,6]
输出:0
class Solution {
public:int longestWPI(vector<int>& hours) {//等价于nums[i]-nums[j]>0 && max(length)unordered_map<int, int> map;map[0]=-1;int sumNum=0;int length=0;for(int i=0; i<hours.size(); i++){sumNum += (hours[i]>8)?1:-1;if(sumNum>0){length = max(length,i+1);}else{if(map.count(sumNum-1)){length = max(length,i-map[sumNum-1]);} }//避免覆盖第一次出现的位置,因为i-map[sumNum-1]是需要返回最长的也就是最早出现的作为起点if(!map.count(sumNum)){map[sumNum]=i;}}return length;}
};





![[JAVAEE] 面试题(四) - 多线程下使用ArrayList涉及到的线程安全问题及解决](https://i-blog.csdnimg.cn/direct/bc453b917f6144c2b17ee8447b99ea6f.png)