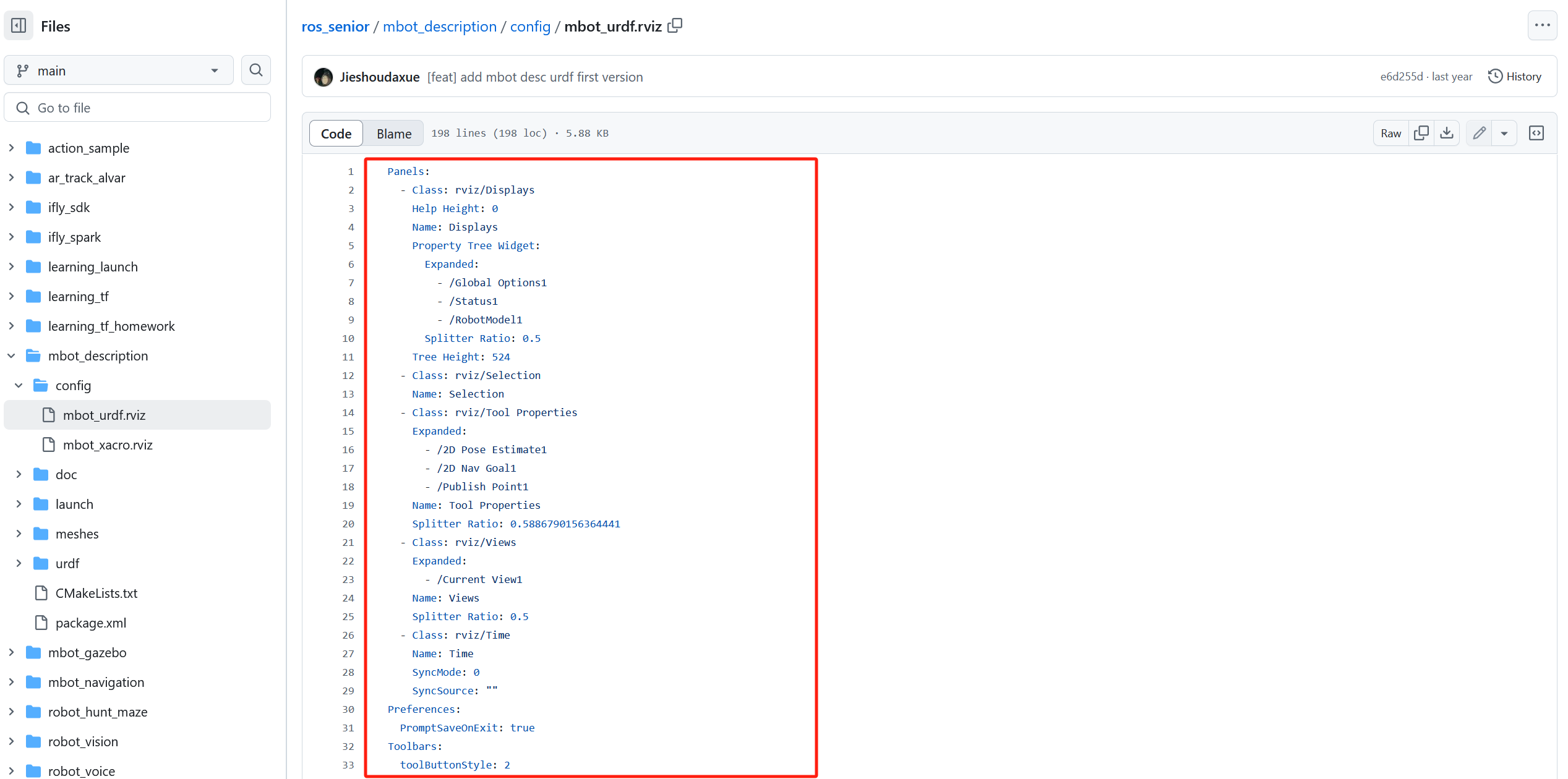
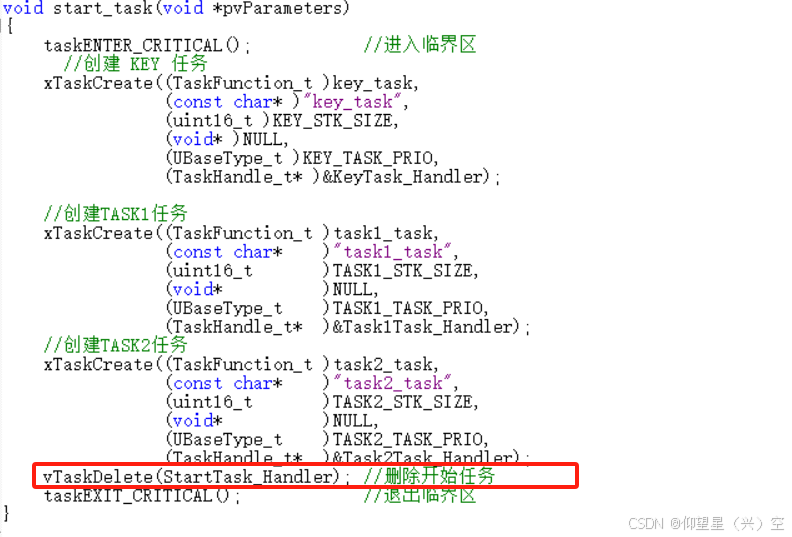
基本内容
提高在有序的数组中查找满足某一条件的索引
-
二分查找的基本类型
① 有多种情况满足条件,找到满足条件的最右索引,例如找到值为4的最右索引(也可以换为小于5的最后一个元素)

② 有多种情况满足条件,找到满足条件的最左索引,例如找到大于4的第一个元素…
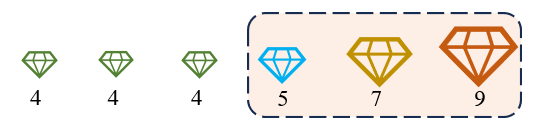
③ 仅存在一种满足条件的情况,①、②代码都适用
[!note]
可以发现,针对①、②两种情况,可以有不同的问法,例如在②情况中,也可以适用于找到4的最后一个元素,只需要在找到的索引上
减一即可找到
- 基本模板
① 情况
def binary_search(self, l, r, target): while l < r:mid = (l + r + 1) // 2 if 满足条件:l = mid # 因为可能是最右情况,所以要保持不变,不能是 mid + 1, 又因为是需要找到最右情况,所以需要通过l往r逼近else:r = mid - 1return l
② 情况
def binary_search(self, l, r, target): target = lwhile l < r:mid = (l + r) // 2 if 满足条件:r = mid #需要找到最左的情况,所以需要通过r往l逼近else:l = mid + 1 return l
- 入门例子
查找有序数列中值为4的最后一个元素,[1,3,4,4,4,4,6,8,9]
可以用①、②两种代码解决
条件为小于等于4为情况①
def binary_search(self, l, r, target): while l < r:mid = (l + r + 1) // 2 if array[mid] <= 4:l = mid else:r = mid - 1return l
条件为大于4为情况②,只需在最后输出的时候进行减一操作
def binary_search(self, l, r, target): target = lwhile l < r:mid = (l + r) // 2 if array[mid] > 4:r = midelse:l = mid + 1 return l - 1 # 因为找到的是大于4的第一个元素6,所以还需要减一操作
题目
二分查找往往需要和其他类型的算法结合,所以题目所需涉及的内容不只是二分查找
- 3261. 统计满足 K 约束的子字符串数量 II
滑动窗口 前缀和 二分查找
class Solution:def __init__(self):self.lefts = Noneself.pre = Nonedef binary_search(self, l, r):target = lwhile l < r:mid = (l + r) // 2 if self.lefts[mid] > target:r = midelse:l = mid + 1return l - 1def countKConstraintSubstrings(self, s: str, k: int, queries: List[List[int]]) -> List[int]:self.pre = [0] * (1 + len(s))self.lefts = [-1] * len(s)left = 0cnt = [0, 0]ans = []for right, x in enumerate(s):cnt[ord(x) % 2] += 1while cnt[0] > k and cnt[1] > k: cnt[ord(s[left]) % 2] -= 1left += 1self.lefts[right] = leftself.pre[right + 1] = self.pre[right] + (right - left + 1)for i,j in queries:if i > self.lefts[j] :ans.append( (j - i + 2)*( j -i + 1)//2)else:h = self.binary_search(i, j)ans.append(self.pre[j+1] - self.pre[h+1] + (h-i + 2)*(h-i +1)//2)return ans